Як виконати частковий тест f в excel
Частковий F-тест використовується, щоб визначити, чи є статистично значуща різниця між моделлю регресії та вкладеною версією тієї самої моделі.
Вкладена модель — це просто модель, яка містить підмножину змінних предикторів у загальній моделі регресії.
Наприклад, припустімо, що ми маємо таку модель регресії з чотирма змінними предикторів:
Y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4 + ε
Прикладом вкладеної моделі може бути наступна модель лише з двома початковими змінними предиктора:
Y = β 0 + β 1 x 1 + β 2 x 2 + ε
Щоб визначити, чи істотно відрізняються ці дві моделі, ми можемо виконати частковий F-тест, який обчислює наступну статистику F-тесту:
F = (( Скорочений RSS – Повний RSS)/p) / ( Повний RSS /nk)
золото:
- Скорочений RSS : Залишкова сума квадратів зменшеної (тобто «вкладеної») моделі.
- RSS full : Залишкова сума квадратів повної моделі.
- p: кількість предикторів, видалених із повної моделі.
- n: загальна кількість спостережень у наборі даних.
- k: кількість коефіцієнтів (включаючи відрізок) у повній моделі.
Цей тест використовує такі нульові та альтернативні гіпотези :
H 0 : усі коефіцієнти, видалені з повної моделі, дорівнюють нулю.
H A : принаймні один із коефіцієнтів, вилучених із повної моделі, відмінний від нуля.
Якщо p-значення , що відповідає статистиці F-критерію, нижче певного рівня значущості (наприклад, 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що принаймні один із коефіцієнтів, вилучених із повної моделі, є значущим.
У наступному прикладі показано, як виконати частковий F-тест у Excel.
Приклад: частковий тест F в Excel
Припустимо, що в Excel є такий набір даних:
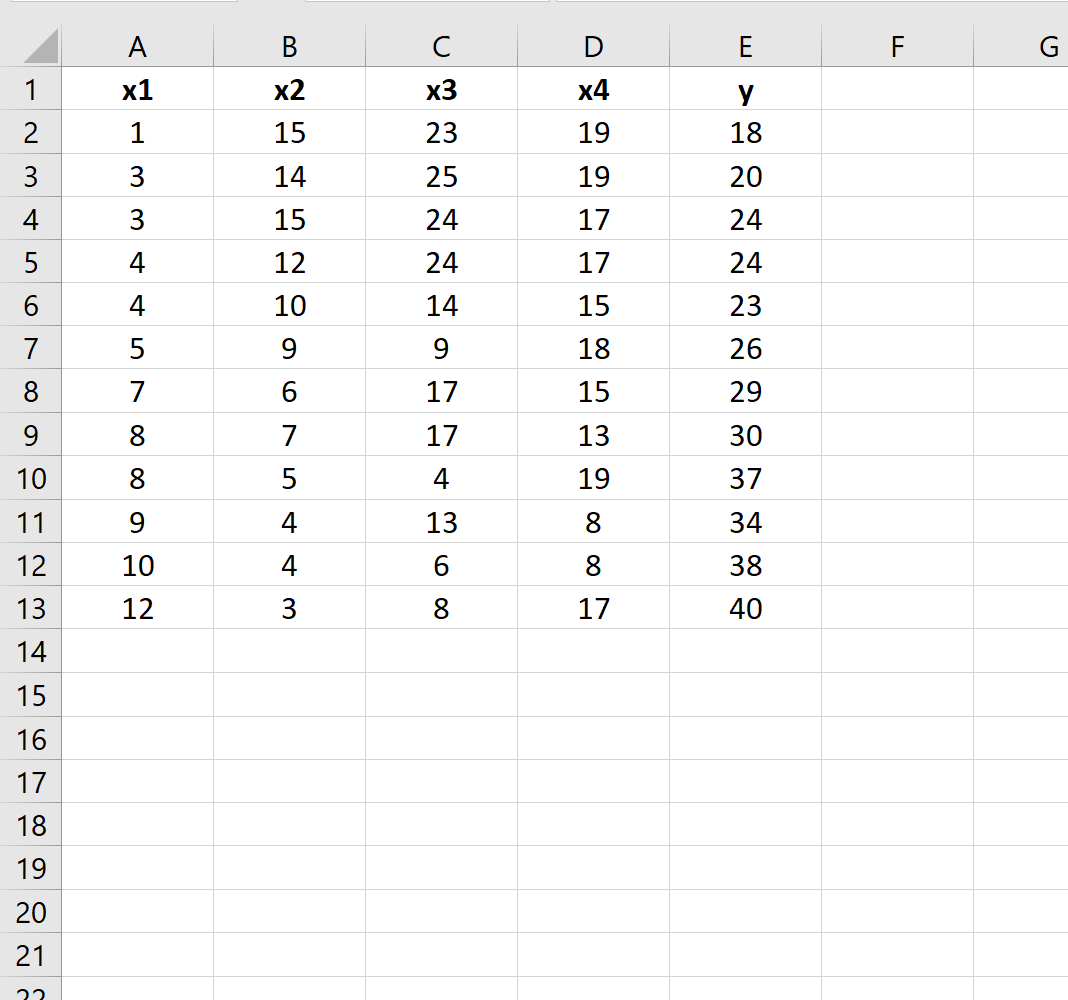
Припустімо, ми хочемо визначити, чи є різниця між наступними двома моделями регресії:
Повна модель: y = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 4 x 4
Скорочена модель: y = β 0 + β 1 x 1 + β 2 x 2
Ми можемо виконати множинну лінійну регресію в Excel для кожної моделі, щоб отримати такий результат:
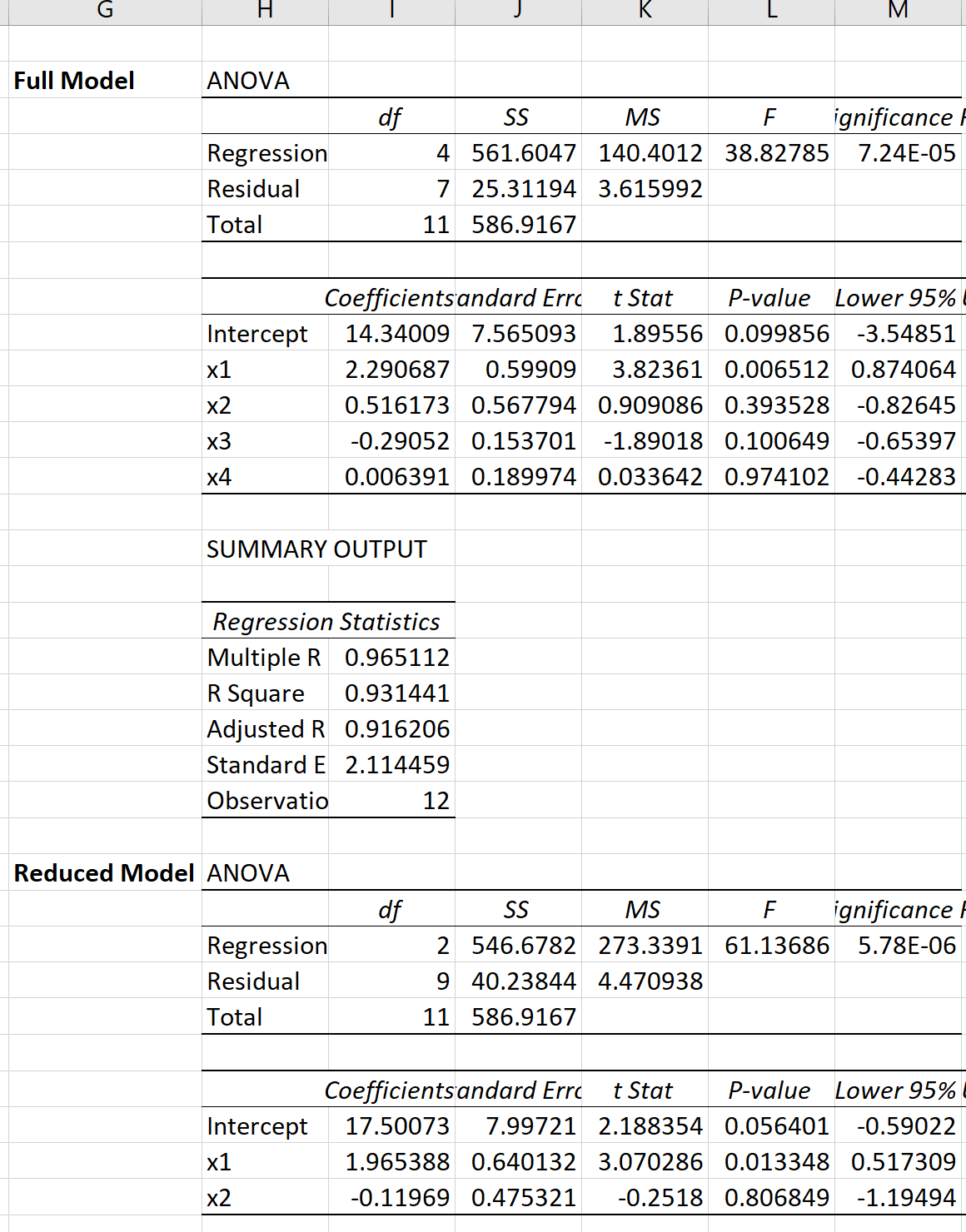
Потім ми можемо використати наступну формулу для обчислення статистики F-тесту для часткового F-тесту:
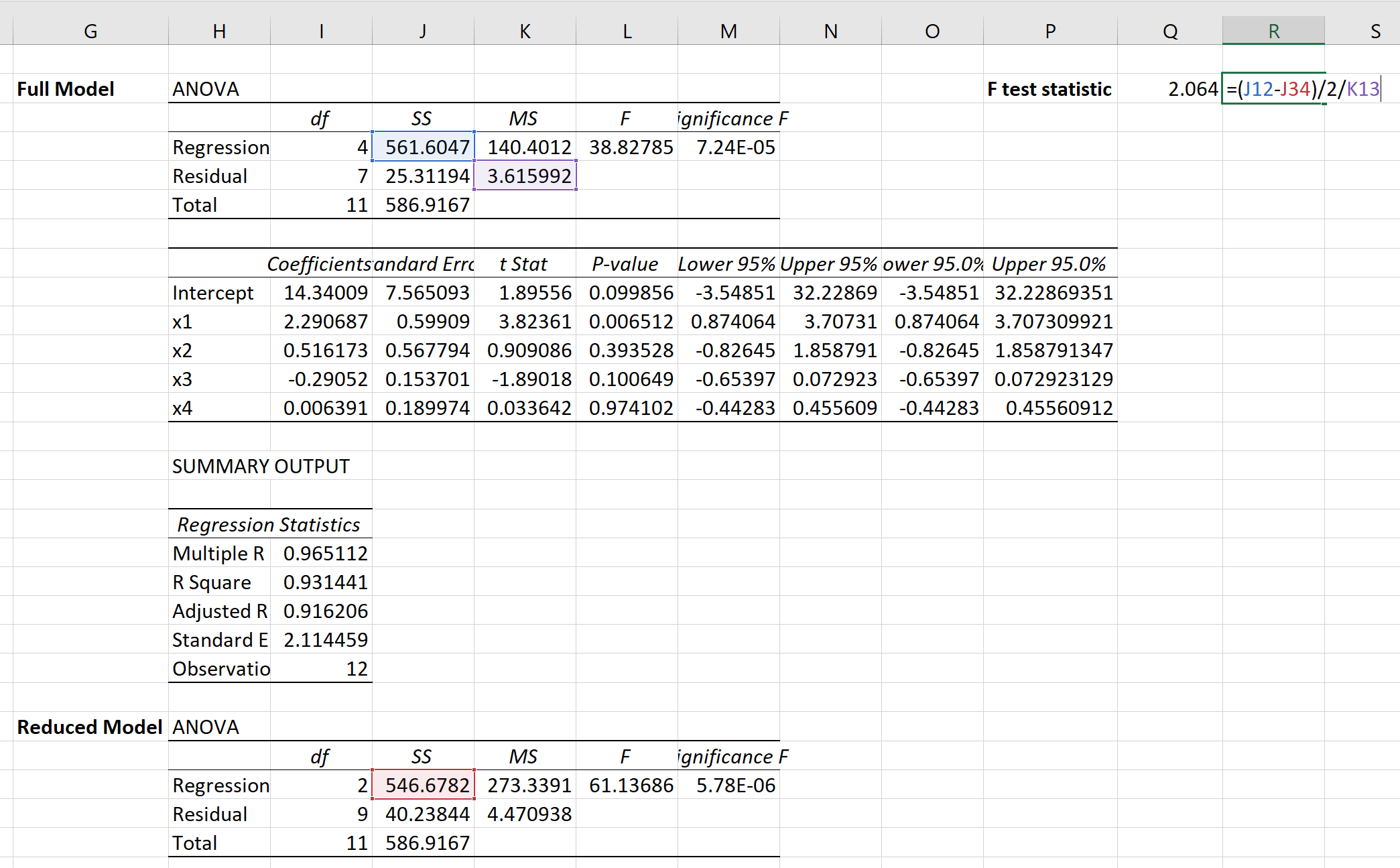
Статистика тесту виявляється 2,064 .
Потім ми можемо використати наступну формулу для обчислення відповідного значення p:
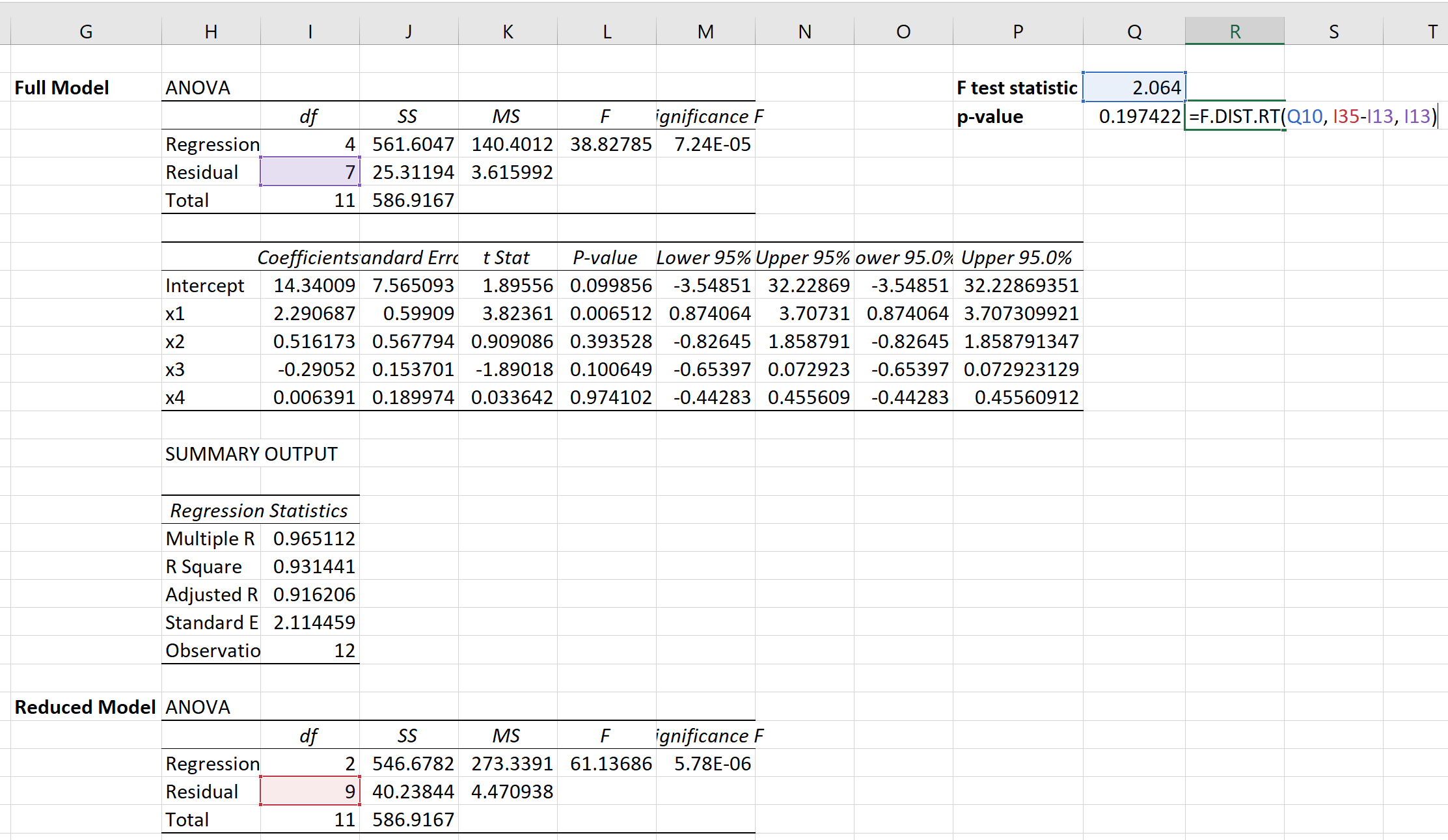
P-значення виявляється рівним 0,1974 .
Оскільки це p-значення не менше 0,05, ми не зможемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що будь-яка із змінних предикторів x3 або x4 є статистично значущою.
Іншими словами, додавання x3 і x4 до регресійної моделі не покращує суттєво відповідність моделі.
Додаткові ресурси
Як виконати просту лінійну регресію в Excel
Як виконати множинну лінійну регресію в Excel
Як обчислити стандартну помилку регресії в Excel
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше