Чому стандартне відхилення важливе? (пояснення + приклади)

Стандартне відхилення використовується для вимірювання розподілу значень у вибірці.

Ми можемо використати таку формулу, щоб обчислити стандартне відхилення заданої вибірки:

√ Σ(x _i – x _bar ) ² / (n-1)

золото:

• Σ: символ, що означає «сума»
• x _i : ^i-те значення вибірки
• x _бар : Зразок означає
• n: розмір вибірки

Чим вище значення стандартного відхилення, тим більше розсіяні значення у вибірці. І навпаки, чим менше значення стандартного відхилення, тим тісніше кластеризовані значення.

Питання, яке студенти часто задають: чому стандартне відхилення важливо?

Відповідь: стандартне відхилення важливе, оскільки воно повідомляє нам про розподіл значень у заданому наборі даних.

ми аналізуємо набір даних Щоразу, коли ми хочемо знайти такі показники:

• Центр набору даних . Найпоширенішим способом вимірювання «центру» є використання середнього значення та медіани.
• Розподіл значень у наборі даних . Найпоширенішим способом вимірювання спреду є використання стандартного відхилення.

Знаючи, де знаходиться центр і який розподіл значень, ми можемо добре зрозуміти розподіл значень у будь-якому наборі даних.

Наступні приклади ілюструють важливість стандартного відхилення на практиці.

Приклад 1: Розподіл зарплати

Припустимо, що середня зарплата в компанії А становить 80 000 доларів, а стандартне відхилення – 20 000 доларів. Оскільки стандартне відхилення настільки велике, немає ніякої гарантії, що вам будуть платити близько 80 000 доларів на рік, якщо ви працюєте в цій компанії, оскільки існує така варіація в зарплатах.

І навпаки, припустімо, що середня зарплата в компанії B також становить 80 000 доларів, але стандартне відхилення становить лише 4 000 доларів. Оскільки це стандартне відхилення дуже мале, ви можете бути впевнені, що вам заплатять близько 80 000 доларів США, оскільки зарплати дуже незначні.

Якби ми створили коробковий графік для візуалізації розподілу зарплати в цих двох компаніях, він міг би виглядати так:

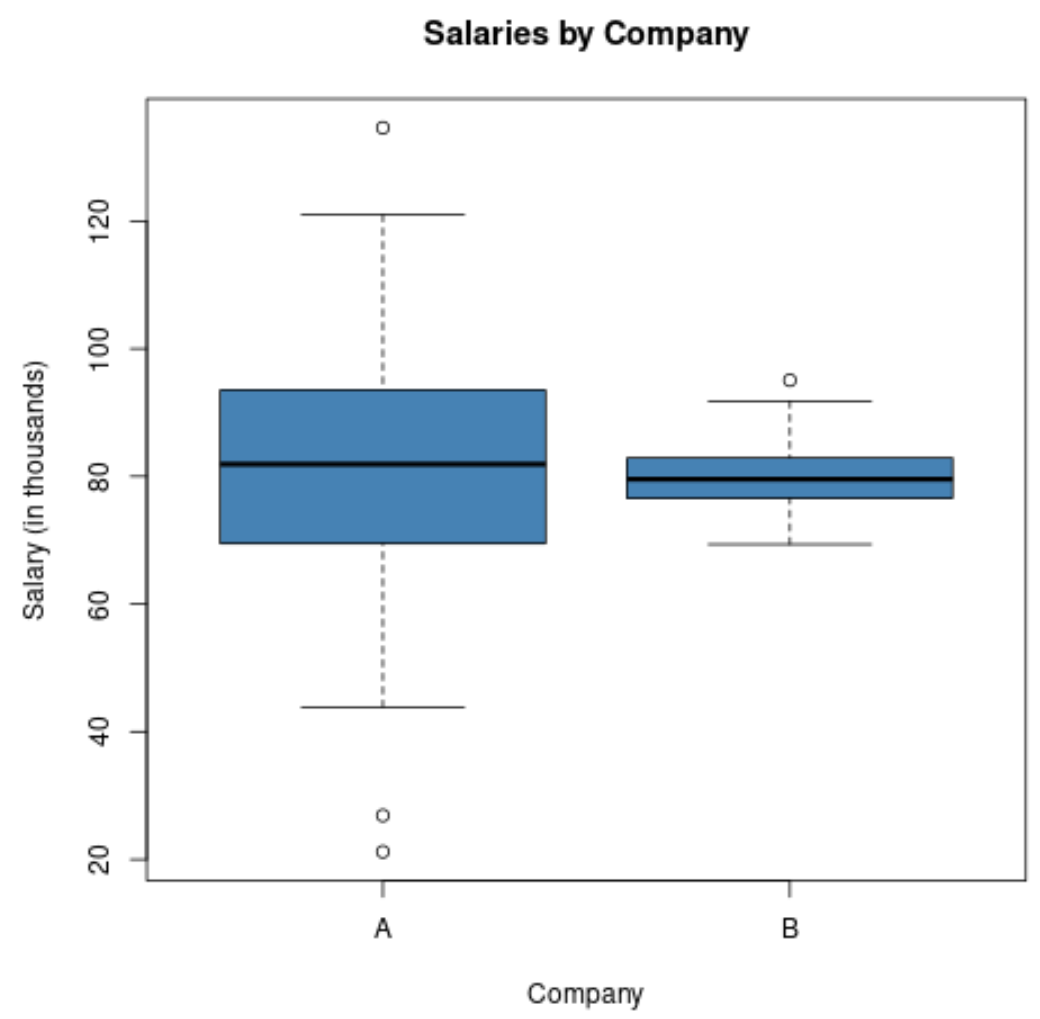
Зверніть увагу, що довжина прямокутної діаграми для компанії А більша, оскільки стандартне відхилення заробітної плати набагато вище.

Обидві компанії мають однакову середню заробітну плату, але розрив у заробітній платі набагато вищий у компанії А.

Приклад 2: Розподіл цін на житло

Припустимо, що середня ціна житла в районі А становить 250 000 доларів, а стандартне відхилення – 50 000 доларів. Оскільки стандартне відхилення досить велике, це означає, що ціни на деякі будинки будуть значно вищими за 250 000 доларів США, а інші – значно нижчими. Якщо ви подивіться на будь-який будинок у цьому районі, немає гарантії, що ціна буде десь близькою до середньої.

І навпаки, припустимо, що середня ціна будинку в районі B також становить 250 000 доларів, але стандартне відхилення становить лише 10 000 доларів. Оскільки це стандартне відхилення досить мале, ви можете бути впевнені, що будь-який будинок, який ви подивитеся поблизу, швидше за все, буде закритий за цією ціною.

Якби ми створили коробкову діаграму для візуалізації розподілу цін на житло в цих двох районах, це могло б виглядати так:

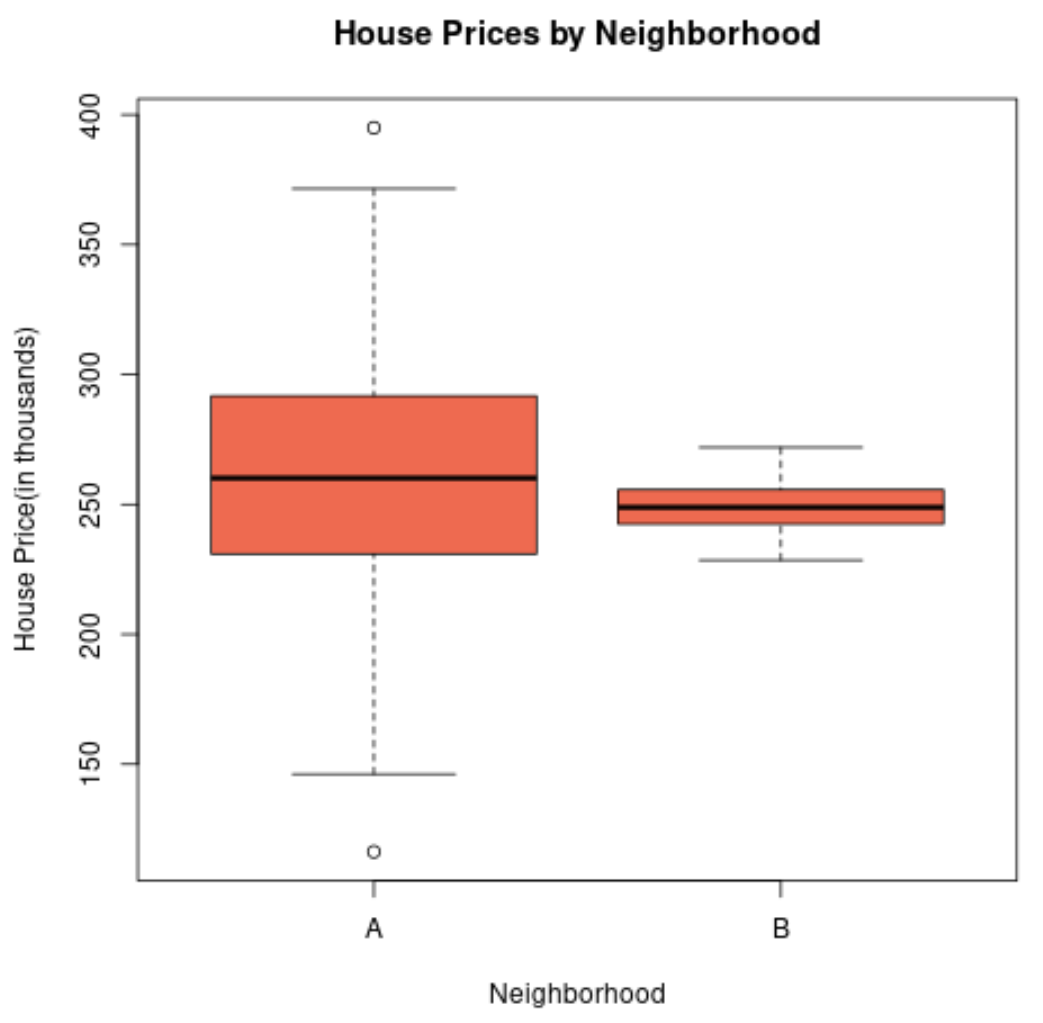
Довжина прямокутної ділянки району A більша, оскільки стандартне відхилення цін на нерухомість набагато вище.

Насправді ціни на житло коливаються від менш ніж 150 000 доларів США до понад 400 000 доларів США для мікрорайону A, тоді як ціни коливаються лише приблизно від 230 000 до 270 000 доларів США для району B.

Просто знаючи стандартне відхилення цін на житло в кожному районі, ми можемо знати, на які варіації можна очікувати в цінах у кожному районі.

Додаткові ресурси

Що вважається хорошим стандартним відхиленням?
Діапазон проти Стандартне відхилення: коли використовувати кожне
Коефіцієнт варіації проти стандартного відхилення: різниця