Що означає високе значення f у anova?
Односторонній дисперсійний аналіз ANOVA використовується для визначення того, чи рівні середні три чи більше незалежних груп.
Односторонній ANOVA використовує такі нульові та альтернативні гіпотези:
- H 0 : Усі групові середні рівні.
- H A : Принаймні одне групове середнє значення відрізняється від інших.
Кожного разу, коли ви виконуєте односторонній дисперсійний аналіз, ви отримаєте зведену таблицю, яка виглядає так:
| Джерело | Сума квадратів (SS) | df | Середні квадрати (MS) | Ф | Р-значення |
|---|---|---|---|---|---|
| Лікування | 192.2 | 2 | 96.1 | 2,358 | 0,1138 |
| Помилка | 1100,6 | 27 | 40.8 | ||
| Всього | 1292,8 | 29 |
Значення F у таблиці розраховується наступним чином:
- Значення F = обробка середніх квадратів / помилка середніх квадратів
Інший спосіб написати це:
- F-значення = варіація між середніми значеннями вибірки / варіація всередині вибірки
Якщо варіація між вибірковими середніми є високою порівняно з варіацією в кожній із вибірок, тоді значення F буде великим.
Наприклад, значення F у таблиці вище обчислюється таким чином:
- F-значення = 96,1 / 40,8 = 2,358
Щоб знайти p-значення , яке відповідає цьому F-значенню, ми можемо використати калькулятор F-розподілу зі ступенями свободи в чисельнику = df Лікування та ступенями свободи в знаменнику = df Помилка.
Наприклад, p-значення, яке відповідає F-значенню 2,358, чисельник df = 2, а знаменник df = 27 дорівнює 0,1138 .
Оскільки це p-значення не менше α = 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що немає статистично значущої різниці між середніми значеннями трьох груп.
Перегляньте значення F дисперсійного аналізу
Щоб отримати інтуїтивне розуміння значення F у таблиці ANOVA, розглянемо наступний приклад.
Припустімо, ми хочемо виконати односторонній дисперсійний аналіз, щоб визначити, чи дають три різні методи навчання різні середні оцінки іспиту. У наступній таблиці показано результати іспиту 10 студентів, які використовували кожну техніку:
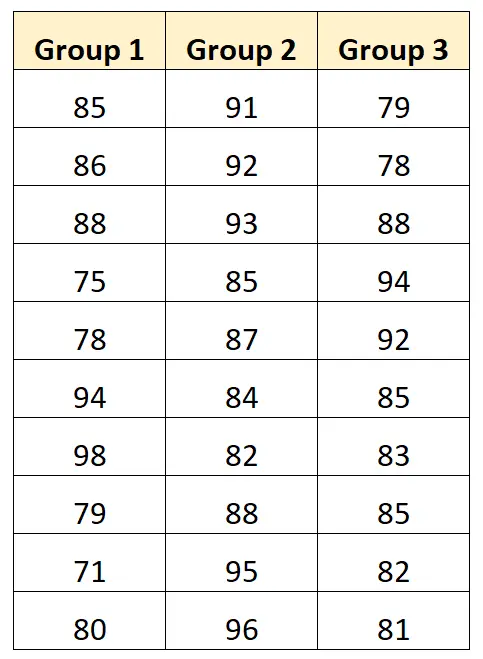
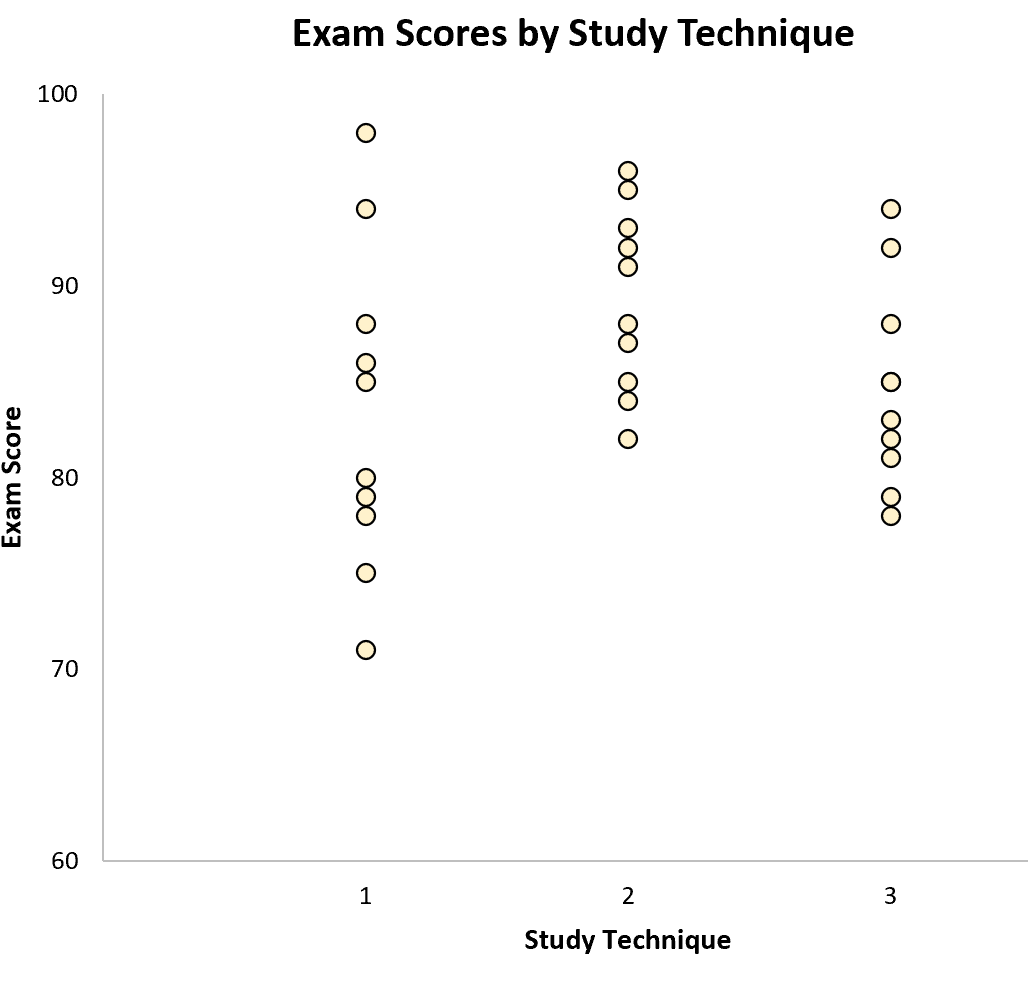
Ми можемо створити наступну діаграму для візуалізації результатів іспиту по групах:
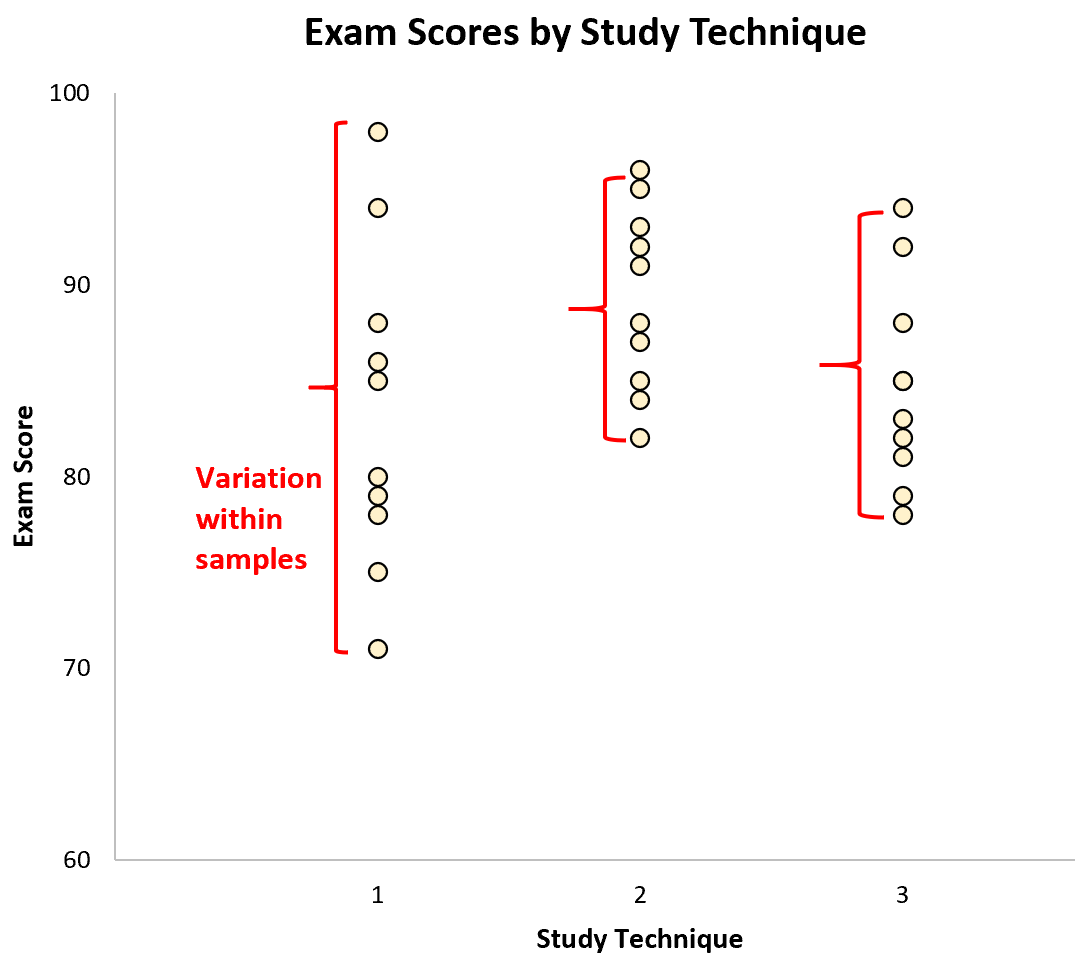
Варіація всередині вибірки представлена розподілом значень всередині кожної окремої вибірки:
Варіація між вибірками представлена відмінностями між вибірковими середніми:
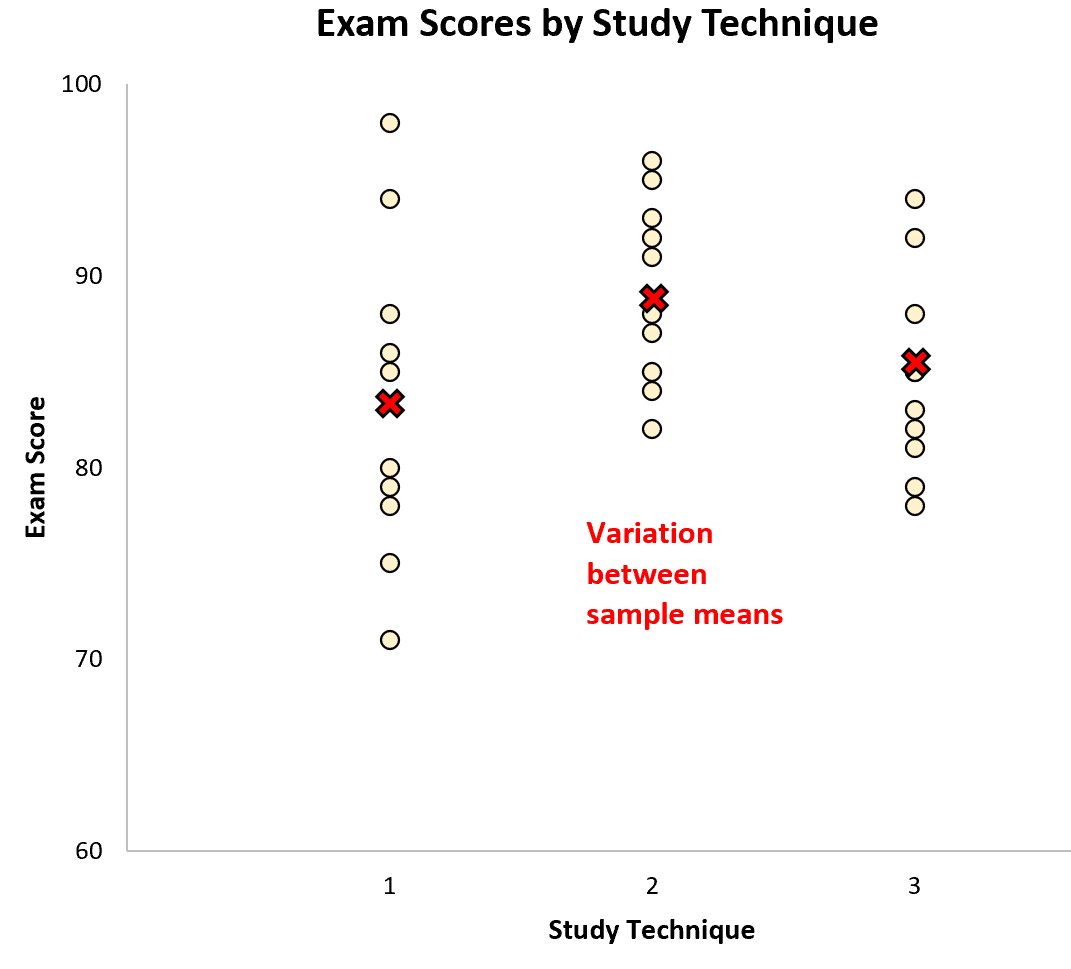
Виконуючи односторонній дисперсійний аналіз для цього набору даних, ми виявили, що значення F становить 2,358 , а відповідне значення p — 0,1138 .
Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що використана методика дослідження призводить до статистично значущих відмінностей у середніх іспитових балах.
Іншими словами, це говорить нам про те, що варіація між вибірковими середніми є недостатньо високою відносно варіації всередині вибірки, щоб відхилити нульову гіпотезу.
Висновок
Ось короткий виклад основних моментів цієї статті:
- Значення F у ANOVA розраховується як: варіація між середніми значеннями вибірки / варіація всередині вибірки.
- Чим вище значення F у ANOVA, тим більша варіація між вибірковими середніми значеннями відносно варіацій у межах вибірки.
- Чим вище значення F, тим менше відповідне значення p.
- Якщо p-значення нижче певного порогу (наприклад, α = 0,05), ми можемо відхилити нульову гіпотезу ANOVA та зробити висновок про наявність статистично значущої різниці між груповими середніми значеннями.
Додаткові ресурси
Як виконати односторонній дисперсійний аналіз в Excel
Як вручну виконати односторонній дисперсійний аналіз
Односторонній калькулятор ANOVA