Якість підгонки
У цій статті пояснюється, що таке відповідність статистики. Крім того, він показує, як виміряти відповідність моделі регресії, і, крім того, ви зможете побачити розв’язану вправу відповідності.
Що таке придатність?
У статистиці відповідність – це те, наскільки регресійна модель відповідає вибірці даних. Іншими словами, відповідність регресійної моделі відноситься до рівня зв’язку між набором спостережень і значеннями, отриманими за допомогою регресії.
Отже, чим краще відповідає регресійна модель, тим краще вона пояснює досліджувані дані. Таким чином, ми хочемо, щоб статистична модель краще відповідала.
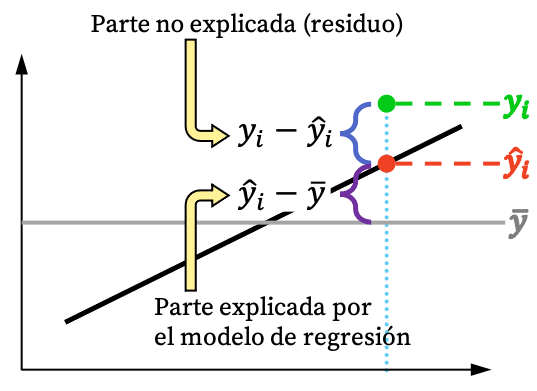
Як ви можете бачити на зображенні вище, значення спостереження зазвичай не можна повністю пояснити регресійною моделлю. Але за логікою, чим більше регресійна модель може пояснити на основі набору даних, тим краще вона підійде. Коротше кажучи, ми зацікавлені в моделі регресії, яка є максимально жорсткою.
Відповідність регресійної моделі
Щоб визначити відповідність регресійної моделі, зазвичай використовують коефіцієнт детермінації , який є статистичним коефіцієнтом, що вказує на відсоток, пояснений регресійною моделлю. Таким чином, чим вищий коефіцієнт детермінації моделі, тим краще модель буде адаптована до вибірки даних.
![]()
Однак слід зазначити, що чим більше змінних має регресійна модель, тим вищим буде її коефіцієнт детермінації. З цієї причини скоригований коефіцієнт детермінації також часто використовується для вимірювання відповідності моделі. Скоригований коефіцієнт детермінації є варіацією попереднього коефіцієнта, який вказує на відсоток, пояснений регресійною моделлю, штрафуючи за кожну пояснювальну змінну, включену в модель.
![]()
Тому краще використовувати скоригований коефіцієнт детермінації для порівняння двох моделей з низкою різних змінних, оскільки він враховує кількість змінних, включених до моделі.
Нарешті, слід зазначити, що критерій хі-квадрат також можна використовувати для вимірювання відповідності регресійної моделі, хоча зазвичай використовуються значення двох попередніх коефіцієнтів.
Конкретний приклад гарного підходу
Нарешті, ми побачимо завершену вправу з коригування якості, щоб завершити засвоєння цієї статистичної концепції.
- З одним і тим самим рядом даних виконуються дві різні моделі лінійної регресії, результати яких ви можете побачити в наступній таблиці. Яку модель краще використовувати?
| Регресійна модель 1 | Регресійна модель 2 | |
|---|---|---|
| Коефіцієнт детермінації | 57% | 64% |
| Скоригований коефіцієнт детермінації | 49% | 43% |
| Кількість пояснювальних змінних | 3 | 7 |
У цьому випадку ми припускаємо, що обидві моделі задовольняють попередні припущення моделей лінійної регресії, і, отже, нам потрібно лише проаналізувати відповідність моделей.
Регресійна модель 2 має вищий коефіцієнт детермінації, ніж регресійна модель 1, тому апріорі здається кращою регресійною моделлю, оскільки вона здатна краще пояснити вибірку даних.
Однак регресійна модель 2 має 7 незалежних змінних у моделі, тоді як регресійна модель 1 має лише 3. Тому модель 2 буде набагато складнішою та важчою для інтерпретації, ніж перша модель.
Крім того, якщо ми подивимося на скоригований коефіцієнт детермінації, який враховує кількість змінних у моделі, регресійна модель 1 має вищий скоригований коефіцієнт детермінації, ніж регресійна модель 2.
Підсумовуючи, хоча краще використовувати регресійну модель 1, оскільки її скоригований коефіцієнт детермінації вищий, ніж у регресійної моделі 2. Регресійна модель 2 має вищий нескоригований коефіцієнт детермінації, тому що вона включила в регресію набагато більше змінних. модель 1. модель, яка збільшує значення зазначеного коефіцієнта, але ускладнює інтерпретацію моделі та, звичайно, погіршує прогнозування нового значення.
Щоб порівняти моделі з різною кількістю змінних, найкраще використовувати скоригований коефіцієнт детермінації, оскільки він штрафує за кожну змінну, додану до моделі. Як ви бачили в цьому прикладі, згідно з нескоригованим коефіцієнтом детермінації регресійна модель 2 є кращою, однак через скоригований коефіцієнт детермінації ми можемо знати, що регресійна модель 1 насправді краща.