Як використовувати таблицю z (з прикладами)

Z-таблиця — це таблиця, яка повідомляє вам, який відсоток значень опускається нижче певного z-оцінки в стандартному нормальному розподілі.

Z-показник просто повідомляє вам, на скільки стандартних відхилень окреме значення даних падає від середнього. Він розраховується таким чином:

z-оцінка = (x – μ) / σ

золото:

• x: індивідуальне значення даних
• μ: середня популяція
• σ: стандартне відхилення сукупності

У цьому посібнику показано кілька прикладів використання таблиці z.

Приклад 1

Оцінки на певному вступному іспиті до коледжу зазвичай розподіляються із середнім значенням μ = 82 і стандартним відхиленням σ = 8. Приблизно який відсоток студентів набирає нижче 84 балів на іспиті?

Крок 1. Знайдіть z-оцінку.

Спочатку ми знайдемо z-оцінку, пов’язану з іспитовим балом 84:

z-оцінка = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Крок 2. Використовуйте діаграму z, щоб знайти відсоток, який відповідає оцінці z.

Далі ми шукатимемо значення 0,25 у таблиці z:

Близько 59,87% студентів набрали менше 84 балів на цьому іспиті.

Приклад 2

Висота рослин у певному саду зазвичай розподіляється із середнім значенням μ = 26,5 дюймів і стандартним відхиленням σ = 2,5 дюймів. Який приблизно відсоток рослин має висоту понад 26 дюймів?

Крок 1. Знайдіть z-оцінку.

Спочатку ми знайдемо z-показник, пов’язаний із зростом 26 дюймів.

z-показник = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Крок 2. Використовуйте діаграму z, щоб знайти відсоток, який відповідає оцінці z.

Далі ми шукатимемо значення -0,2   в таблиці z:

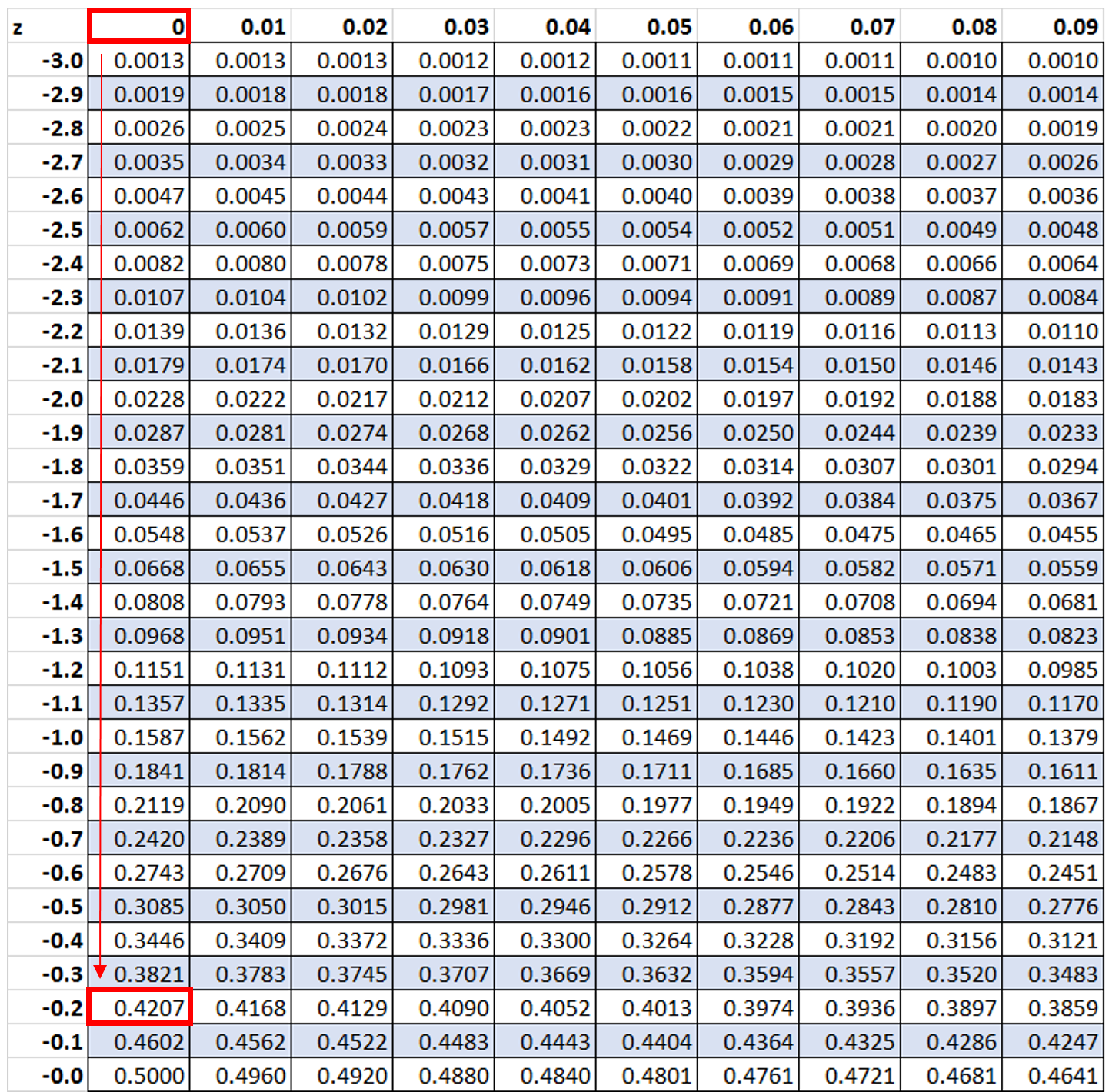
Ми бачимо, що 42,07% значень нижче z-показника -0,2. Однак у цьому прикладі ми хочемо знати, який відсоток значень перевищує -0,2, який ми можемо знайти за формулою 100% – 42,07% = 57,93%.

Таким чином, приблизно 59,87% рослин у цьому саду мають висоту понад 26 дюймів.

Приклад 3

Вага певного виду дельфінів зазвичай розподіляється із середнім значенням μ = 400 фунтів і стандартним відхиленням σ = 25 фунтів. Приблизно який відсоток дельфінів важать від 410 до 425 фунтів?

Крок 1. Знайдіть z-оцінки.

По-перше, ми знайдемо z-показники, пов’язані з 410 та 425 книгами

z-оцінка 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z оцінка 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Крок 2. Використовуйте z-діаграму, щоб знайти відсотки, які відповідають кожному z-балу.

Спочатку ми шукатимемо значення 0,4   в таблиці z:

Далі ми шукатимемо значення 1   в таблиці z:

Нарешті, ми віднімемо найменше значення від найбільшого: 0,8413 – 0,6554 = 0,1859 .

Таким чином, приблизно 18,59% дельфінів важать від 410 до 425 фунтів.

Додаткові ресурси

Введення в нормальний розподіл
Калькулятор нормальної площі розподілу
Калькулятор балів Z