Як інтерпретувати залишкову стандартну помилку

Залишкова стандартна помилка використовується для вимірювання того, наскільки регресійна модель відповідає набору даних.

Простіше кажучи, він вимірює стандартне відхилення залишків у регресійній моделі.

Він розраховується таким чином:

Залишкова стандартна помилка = √ Σ(y – ŷ) ² /df

золото:

• y: спостережуване значення
• ŷ: прогнозоване значення
• df: Ступені свободи, розраховані як загальна кількість спостережень – загальна кількість параметрів моделі.

Чим менша залишкова стандартна помилка, тим краще модель регресії відповідає набору даних. І навпаки, чим вище залишкова стандартна помилка, тим гірше модель регресії відповідає набору даних.

Модель регресії, яка має невелику залишкову стандартну помилку, матиме точки даних, щільно згруповані навколо підігнаної лінії регресії:

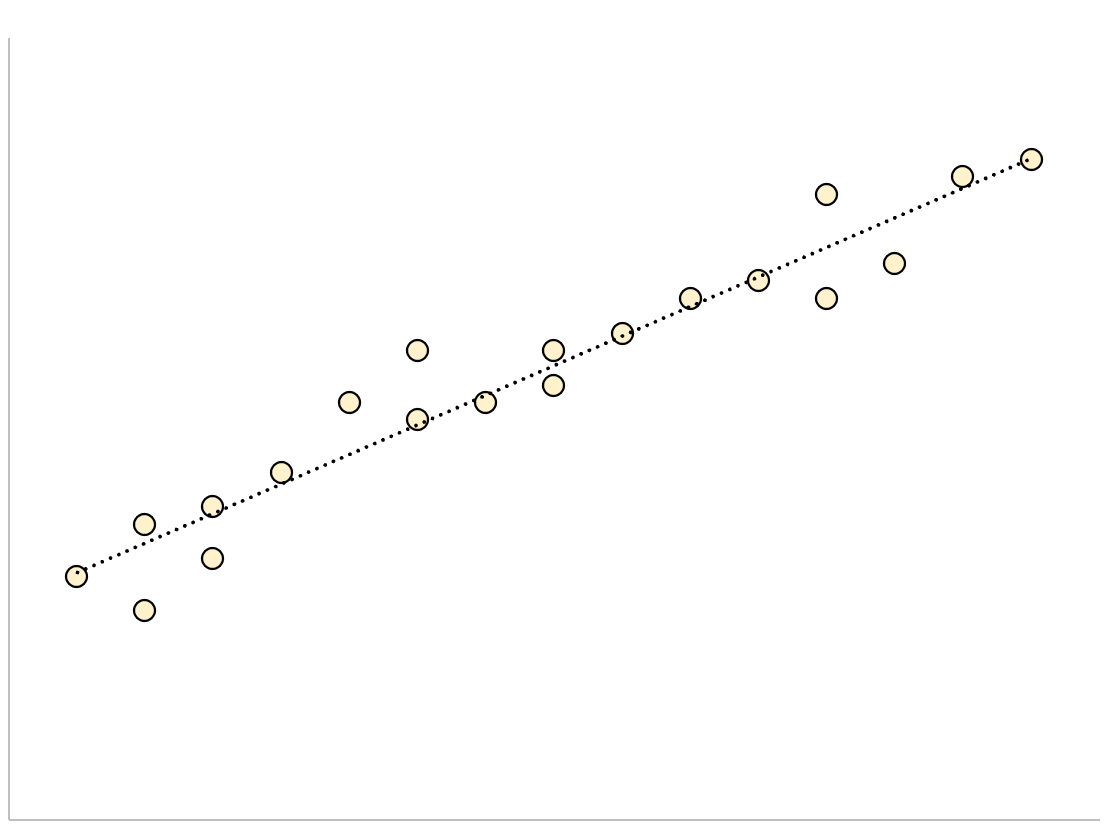
Залишки цієї моделі (різниця між спостережуваними значеннями та прогнозованими значеннями) будуть невеликими, тобто залишкова стандартна помилка також буде невеликою.

І навпаки, регресійна модель, яка має велику залишкову стандартну помилку, матиме точки даних, більш розкидані навколо підігнаної лінії регресії:

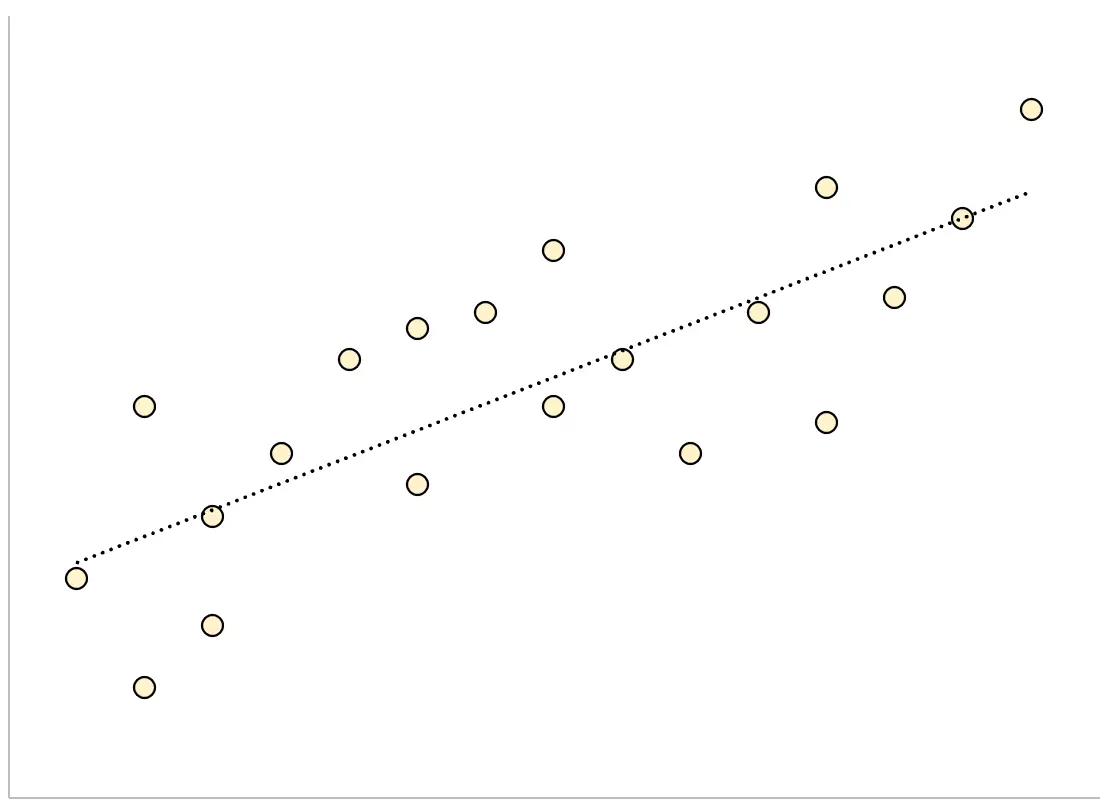
Залишки цієї моделі будуть більшими, що означає, що залишкова стандартна помилка також буде більшою.

У наступному прикладі показано, як обчислити та інтерпретувати залишкову стандартну помилку регресійної моделі в R.

Приклад: Інтерпретація залишкової стандартної помилки

Припустімо, ми хочемо підібрати таку модель множинної лінійної регресії:

mpg = β ₀ + β ₁ (об’єм) + β ₂ (потужність)

Ця модель використовує передбачувані змінні «об’єм» і «кінська сила», щоб передбачити милі на галон, пройдені даним автомобілем.

У наведеному нижче коді показано, як підігнати цю модель регресії в R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

У нижній частині результату ми бачимо, що залишкова стандартна помилка цієї моделі становить 3,127 .

Це говорить нам про те, що регресійна модель прогнозує автомобільний миль на галон із середньою похибкою приблизно 3127.

Використання залишкової стандартної помилки для порівняння моделей

Залишкова стандартна помилка особливо корисна для порівняння відповідності різних регресійних моделей.

Наприклад, припустімо, що ми використовуємо дві різні регресійні моделі для прогнозування миль на галлон автомобіля. Залишкова стандартна помилка кожної моделі така:

• Залишкова стандартна помилка моделі 1: 3,127
• Залишкова стандартна помилка моделі 2: 5,657

Оскільки модель 1 має нижчу залишкову стандартну помилку, вона краще відповідає даним, ніж модель 2. Таким чином, ми б віддавали перевагу використанню моделі 1 для прогнозування миль на галон автомобіля, оскільки прогнози, які вона робить, ближчі до спостережуваних значень миль на галлон автомобілів.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як створити ділянку залишків у R