Як виконати ієрархічну регресію в stata

Ієрархічна регресія — це техніка, яку можна використовувати для порівняння кількох різних лінійних моделей.

Основна ідея полягає в тому, що ми спочатку підбираємо модель лінійної регресії з однією пояснювальною змінною. Далі ми підбираємо іншу регресійну модель, використовуючи додаткову пояснювальну змінну. Якщо R-квадрат (частка дисперсії у змінній відповіді, яку можна пояснити пояснювальними змінними) у другій моделі значно вищий, ніж R-квадрат у попередній моделі, це означає, що друга модель краща.

Потім ми повторюємо процес підгонки додаткових моделей регресії з більшою кількістю пояснювальних змінних і дивимося, чи пропонують нові моделі покращення порівняно з попередніми моделями.

Цей підручник надає приклад виконання ієрархічної регресії в Stata.

Приклад: ієрархічна регресія в Stata

Ми використаємо вбудований набір даних під назвою auto , щоб проілюструвати, як виконувати ієрархічну регресію в Stata. Спочатку завантажте набір даних, ввівши в командне поле наступне:

автоматичне використання системи

Ми можемо отримати короткий підсумок даних за допомогою такої команди:

узагальнити

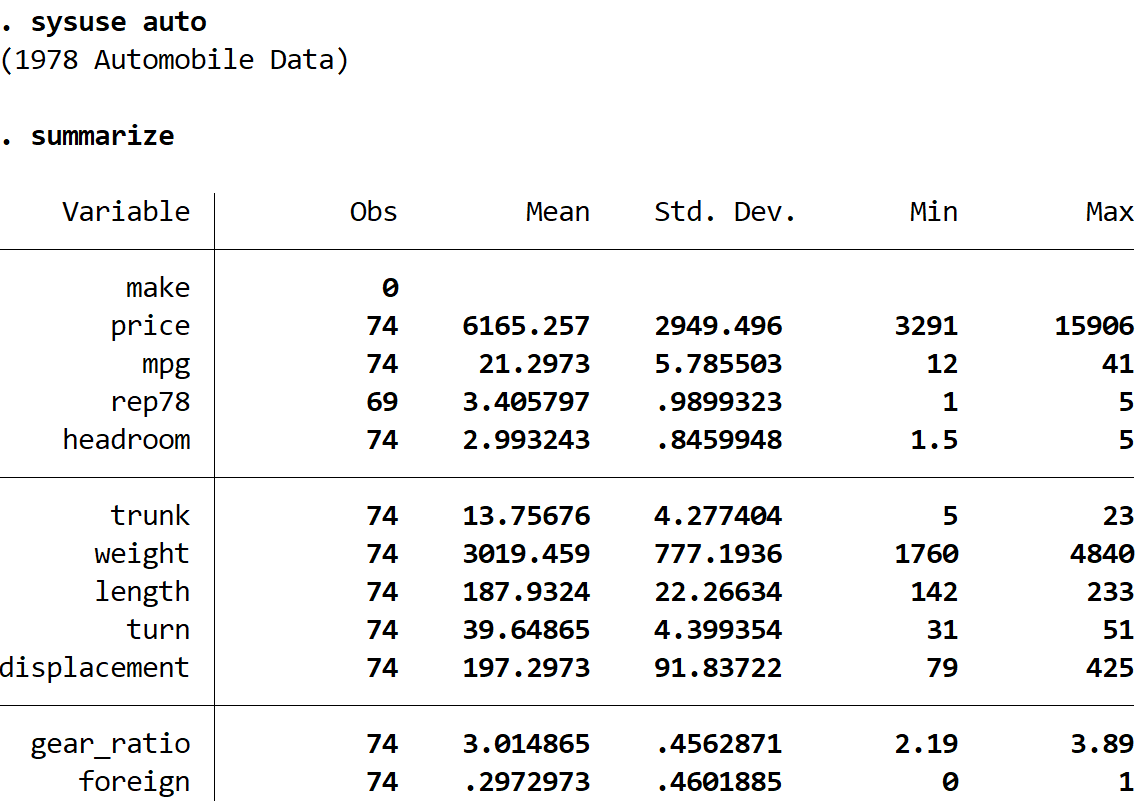
Ми бачимо, що набір даних містить інформацію про 12 різних змінних загалом для 74 автомобілів.

Ми підберемо наступні три моделі лінійної регресії та використаємо ієрархічну регресію, щоб побачити, чи забезпечує кожна наступна модель значне покращення порівняно з попередньою моделлю:

Модель 1: ціна = перехоплення + миль на галлон

Модель 2: ціна = перехоплення + миль на галон + вага

Модель 3: ціна = перехоплення + миль на галон + вага + передавальне число

Щоб виконати ієрархічну регресію в Stata, нам спочатку потрібно встановити пакет Hireg . Для цього введіть наступне в полі команди:

знайти Гірега

У вікні, що з’явиться, натисніть Hireg з https://fmwww.bc.edu/RePEc/bocode/h

У наступному вікні клацніть посилання « Натисніть тут, щоб установити» .

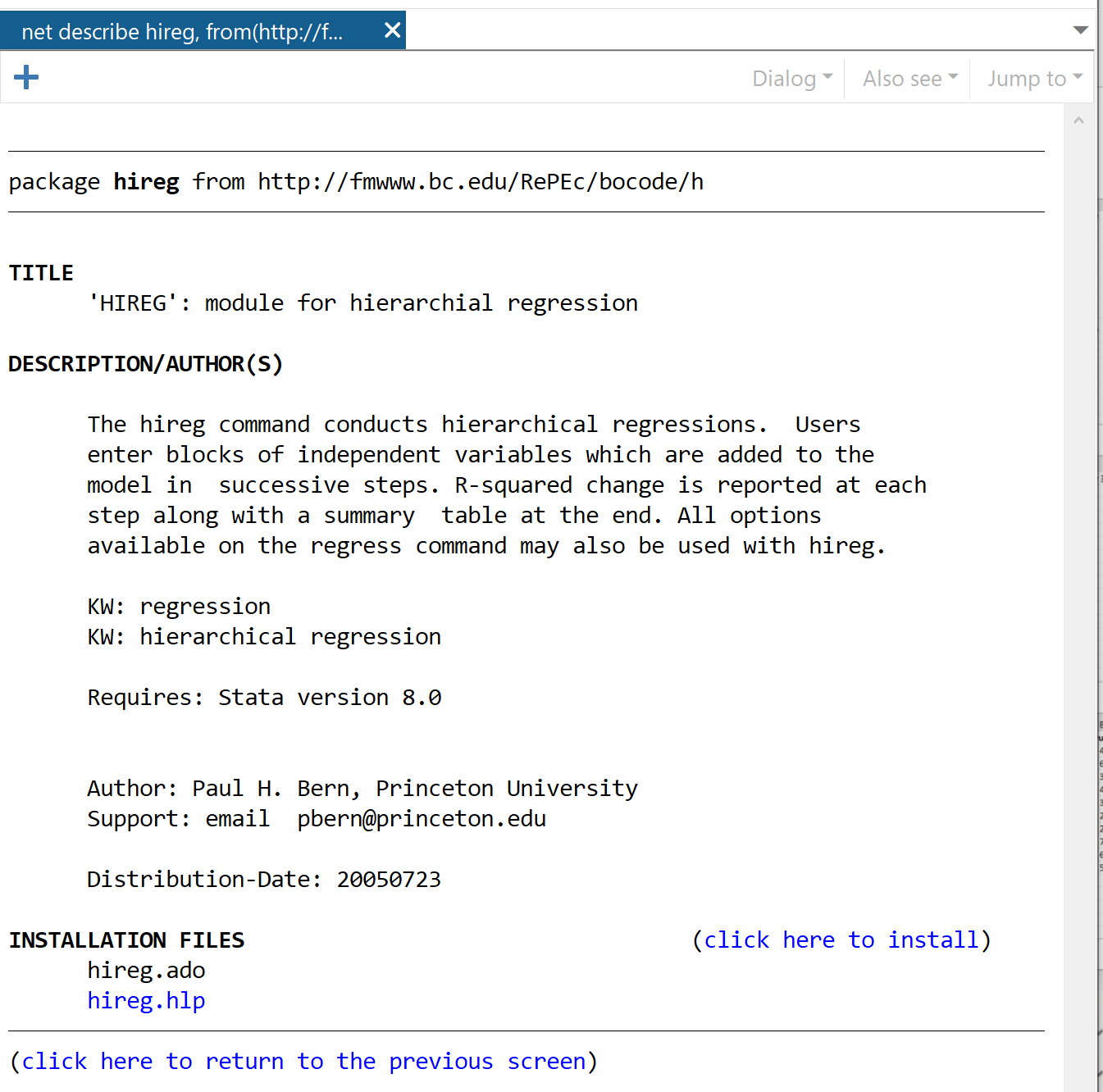
Пакет буде встановлено за лічені секунди. Потім, щоб виконати ієрархічну регресію, ми використаємо таку команду:

ціна оренди (милі на галон) (вага) (передаточне число)

Ось що це вимагає від Stata:

• Виконайте ієрархічну регресію, використовуючи ціну як змінну відповіді в кожній моделі.
• Для першої моделі використовуйте mpg як пояснювальну змінну.
• Для другої моделі додайте вагу як додаткову пояснювальну змінну.
• Для третьої моделі додайте gear_ratio як іншу пояснювальну змінну.

Ось результат першої моделі:

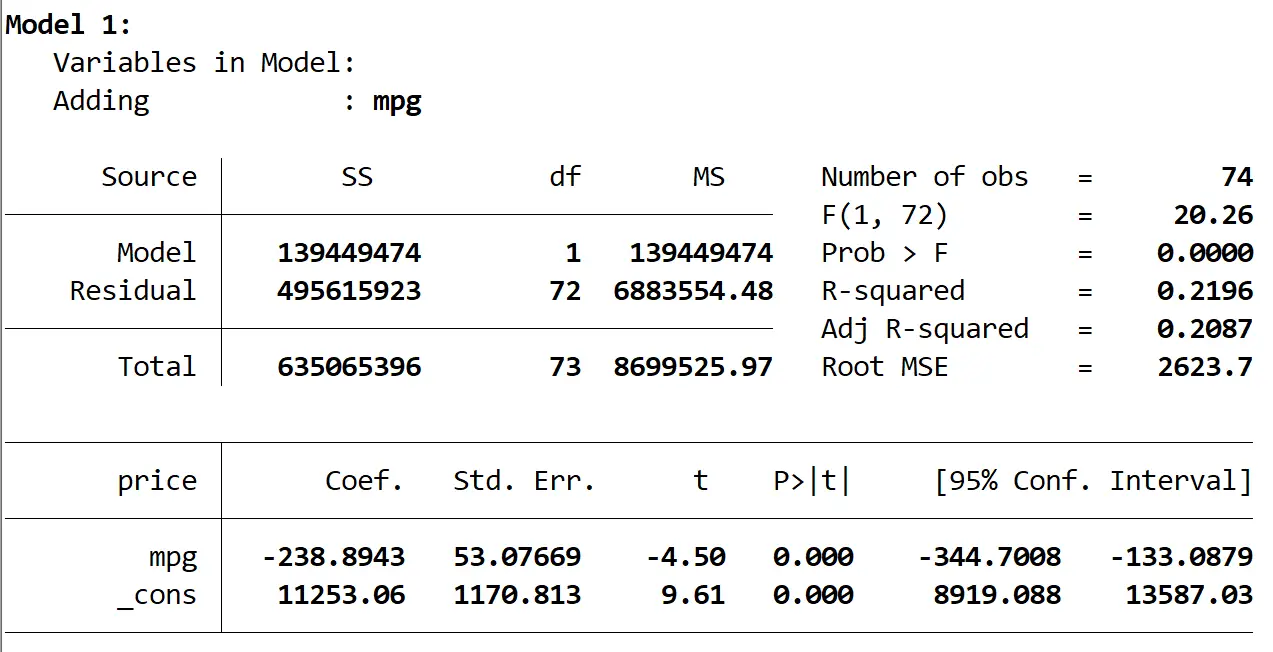
Ми бачимо, що R-квадрат моделі становить 0,2196 , а загальне значення p (Prob > F) моделі становить 0,0000 , що є статистично значущим при α = 0,05.

Далі ми бачимо результат другої моделі:

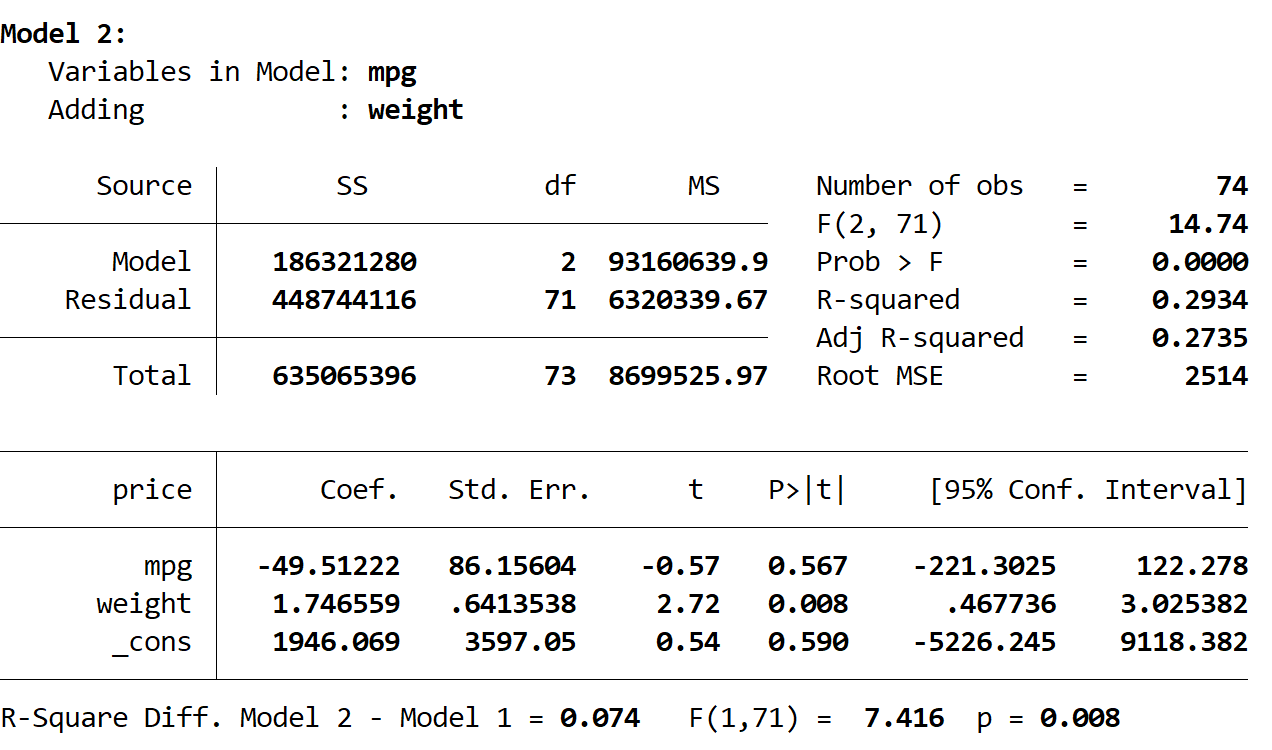
R-квадрат цієї моделі становить 0,2934 , що більше, ніж у першої моделі. Щоб визначити, чи є ця різниця статистично значущою, Stata виконала F-тест, який дав такі числа внизу результату:

• R квадрат різниці між двома моделями = 0,074
• F-статистика для різниці = 7,416
• Відповідне p-значення F-статистики = 0,008

Оскільки p-значення менше 0,05, ми робимо висновок, що в другій моделі є статистично значуще покращення порівняно з першою моделлю.

Нарешті ми можемо побачити результат третьої моделі:

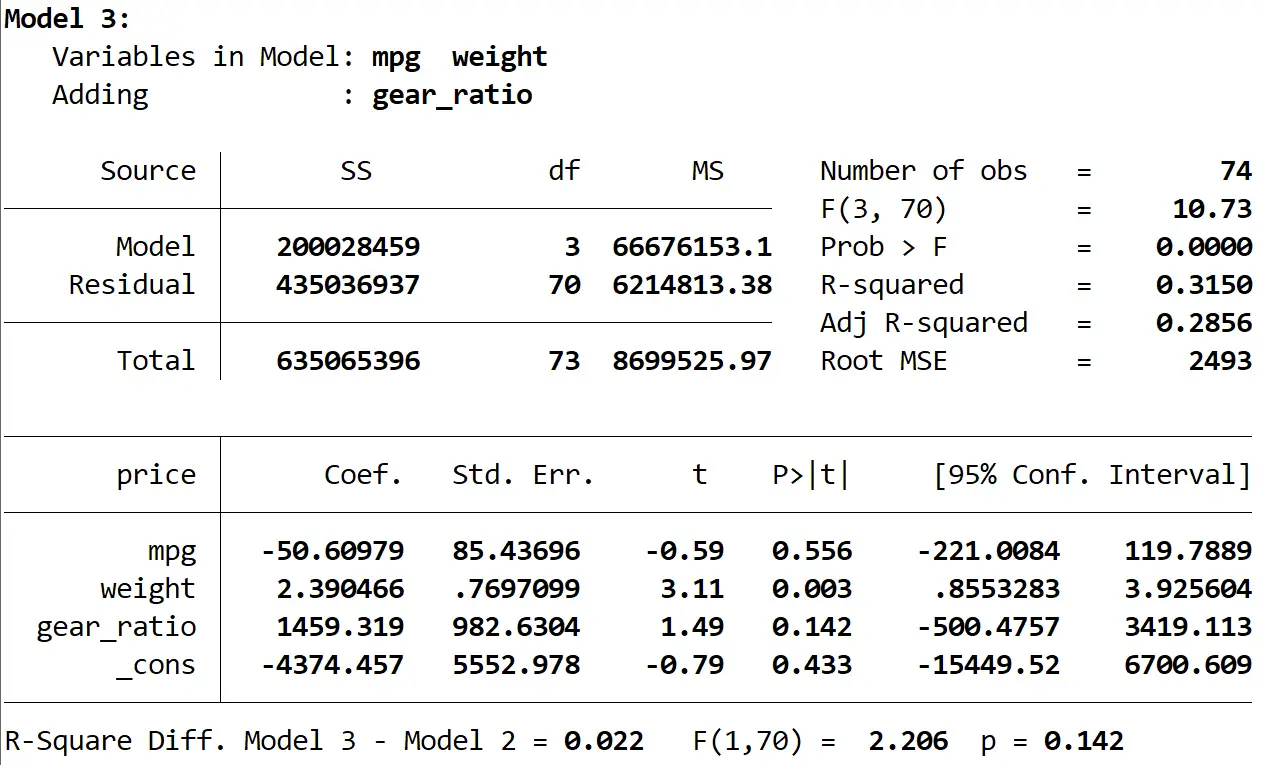
R-квадрат цієї моделі становить 0,3150 , що більше, ніж у другої моделі. Щоб визначити, чи є ця різниця статистично значущою, Stata виконала F-тест, який дав такі числа внизу результату:

• R квадрат різниці між двома моделями = 0,022
• F-статистика для різниці = 2,206
• Відповідне p-значення F-статистики = 0,142

Оскільки p-значення не менше 0,05, ми не маємо достатніх доказів того, що третя модель забезпечує покращення в порівнянні з другою моделлю.

У самому кінці результату ми бачимо, що Stata надає зведення результатів:

У цьому конкретному прикладі можна зробити висновок, що модель 2 запропонувала значне покращення порівняно з моделлю 1, але що модель 3 не запропонувала значного покращення порівняно з моделлю 2.