Як виконати тест тьюкі в r
Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.
Якщо загальне p-значення таблиці ANOVA нижче певного рівня значущості, тоді ми маємо достатньо доказів, щоб стверджувати, що принаймні одне з групових середніх відрізняється від інших.
Однак це не говорить нам , які групи відрізняються одна від одної. Це просто говорить нам про те, що не всі середні групові показники однакові. Для того, щоб точно знати, які групи відрізняються одна від одної, нам потрібно провести ретельний тест .
Одним із найбільш часто використовуваних репресивних тестів є тест Тьюкі , який дозволяє нам виконувати попарні порівняння між середніми значеннями кожної групи, одночасно контролюючи частоту помилок у групі .
Цей підручник пояснює, як виконати тест Tukey у R.
Примітка: якщо будь-яка з груп у вашому дослідженні вважається контрольною групою, ви повинні використовувати тест Даннетта як додатковий тест.
Приклад: тест Тьюкі в R
Крок 1. Підберіть модель ANOVA.
У наведеному нижче коді показано, як створити фальшивий набір даних із трьома групами (A, B і C) і підібрати односторонню модель ANOVA до даних, щоб визначити, чи рівні середні значення кожної групи:
#make this example reproducible set.seed(0) #create data data <- data.frame(group = rep (c("A", "B", "C"), each = 30), values = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data head(data) group values 1 A 2.6900916 2 A 0.7965260 3 A 1.1163717 4 A 1.7185601 5 A 2.7246234 6 A 0.6050458 #fit one-way ANOVA model model <- aov (values~group, data=data) #view the model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) group 2 98.93 49.46 30.83 7.55e-11 *** Residuals 87 139.57 1.60 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Ми бачимо, що загальне p-значення з таблиці ANOVA становить 7,55e-11 . Оскільки це число менше 0,05, у нас є достатньо доказів, щоб стверджувати, що середні значення в кожній групі не однакові. Отже, ми можемо виконати тест Тьюкі, щоб точно визначити, які групові середні відрізняються.
Крок 2: Виконайте тест Тьюкі.
У наступному коді показано, як використовувати функцію TukeyHSD() для виконання тесту Tukey:
#perform Tukey's Test TukeyHSD(model, conf.level= .95 ) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = values ~ group, data = data) $group diff lwr upr p adj BA 0.9777414 0.1979466 1.757536 0.0100545 CA 2.5454024 1.7656076 3.325197 0.0000000 CB 1.5676610 0.7878662 2.347456 0.0000199
P-значення вказує на те, чи є статистично значуща різниця між кожною програмою. Результати показують, що існує статистично значуща різниця між середньою втратою ваги в кожній програмі на рівні значущості 0,05.
Особливо:
- Значення P для різниці середніх між B і A: 0,0100545
- Значення P для різниці середніх між C і A: 0,0000000
- Значення P для різниці середніх між C і B: 0,0000199
Крок 3: Візуалізуйте результати.
Ми також можемо використовувати функцію plot(TukeyHSD()) для візуалізації довірчих інтервалів:
#plot confidence intervals plot(TukeyHSD(model, conf.level= .95 ), las = 2 )
Примітка. Аргумент las визначає, що мітки галочок мають бути перпендикулярними (las=2) до осі.
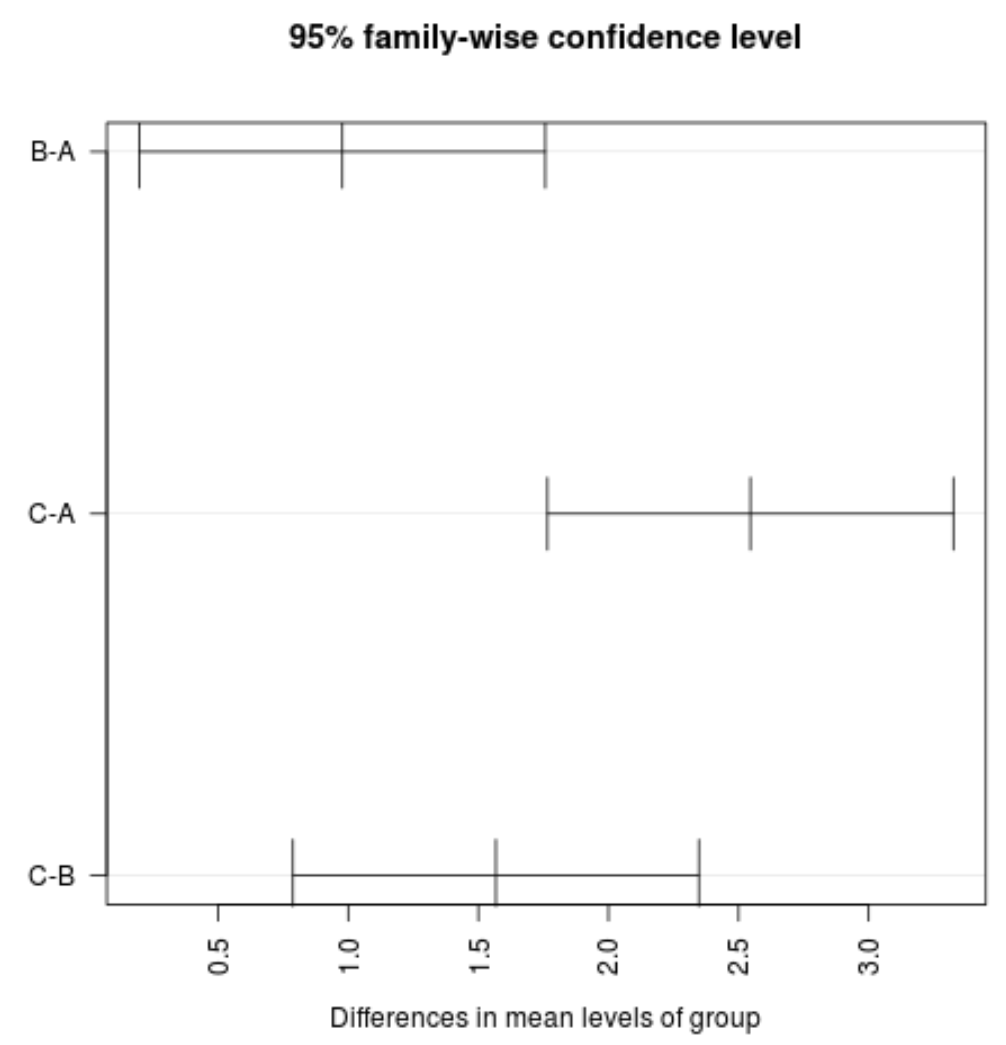
Ми бачимо, що жоден із довірчих інтервалів для середнього значення між групами не містить нульового значення, що вказує на наявність статистично значущої різниці в середніх втратах між трьома групами. Це узгоджується з тим, що всі p-значення для наших перевірок гіпотез менше 0,05.
Для цього конкретного прикладу ми можемо зробити такий висновок:
- Середні значення групи C значно перевищують середні значення груп A і B.
- Середні значення групи В значно перевищують середні значення групи А.
Додаткові ресурси
Посібник із використання пост-хок тестування з ANOVA
Як виконати односторонній дисперсійний аналіз у R
Як виконати двосторонній дисперсійний аналіз у R