Що таке кореляція нульового порядку?
У статистиці кореляція між двома змінними говорить нам про зв’язок між цими двома змінними.
Один із найпростіших типів кореляції відомий як кореляція нульового порядку , яка стосується кореляції між двома змінними без контролю можливого впливу інших змінних.
Прикладом такого типу кореляції є коефіцієнт кореляції Пірсона , який вимірює лінійний зв’язок між двома змінними та може приймати значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Чим далі кореляція від нуля, тим сильніший зв’язок між двома змінними.
Кореляції першого та другого порядку
Якщо ми обчислюємо кореляцію між двома змінними A і B, контролюючи вплив третьої змінної C, ми б назвали кореляцію між A і B кореляцією першого порядку .
Подібним чином, якщо ми обчислюємо кореляцію між двома змінними A і B, контролюючи вплив змінних C і D, ми називатимемо кореляцію між A і B кореляцією другого порядку .
Приклад кореляції нульового порядку
Припустимо, у нас є такий набір даних, який показує кількість годин, витрачених на навчання, і оцінку, отриману на іспиті 10 різними студентами:
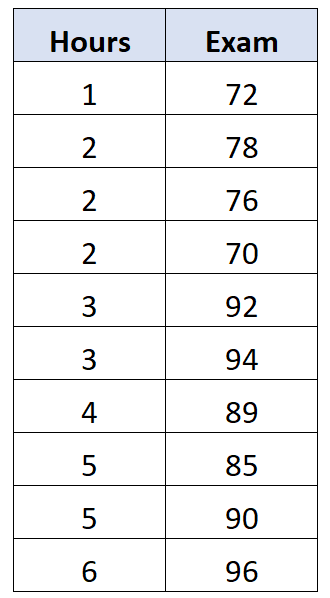
Виявляється, що кореляція між цими двома змінними становить 0,762 . Це вважатиметься кореляцією нульового порядку між двома змінними, оскільки ми не контролюємо потенційний вплив третьої змінної.
Однак насправді можливо, що на зв’язок між цими двома змінними впливають інші фактори.
Наприклад, поточна оцінка студента в класі може вплинути на його іспитовий бал. Припустимо, ми також маємо доступ до цих даних:
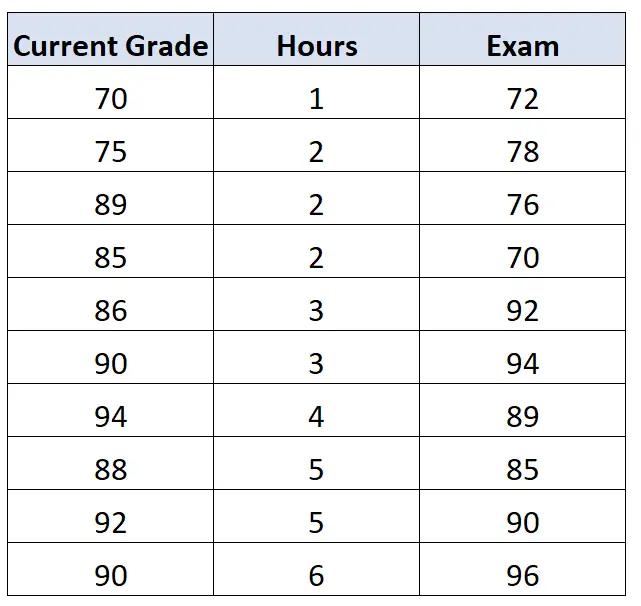
Якщо потім обчислити кореляцію між годинами та іспитом , контролюючи вплив поточної оцінки , ми виявимо, що кореляція першого порядку між годинами та іспитом становить 0,578 .
Це означає, що все ще існує досить сильна позитивна кореляція між вивченими годинами та оцінкою іспиту, навіть після контролю впливу поточної оцінки студента в класі.
Примітка. Кореляцію першого порядку іноді називають частковою кореляцією . У цьому посібнику пояснюється, як обчислити часткові кореляції в Excel.
Кореляції нульового порядку в кореляційній матриці
ми створюємо кореляційну матрицю Щоразу, коли для набору змінних коефіцієнти кореляції, що відображаються в матриці, завжди є кореляціями нульового порядку, оскільки це просто кореляції між кожною попарною комбінацією змінних без урахування впливу інших змінних.
Наприклад, розглянемо наш набір даних із попереднього прикладу:

Якби ми створили кореляційну матрицю для цього набору даних, вона виглядала б так:
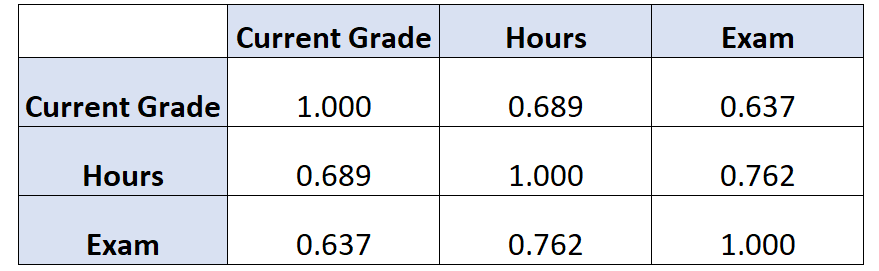
Спосіб інтерпретації цього:
- Співвідношення між поточною оцінкою та вивченими годинами становить 0,689 .
- Кореляція між поточним балом і балом, отриманим на іспиті, становить 0,637 .
- Співвідношення між вивченими годинами та іспитовим балом становить 0,762 .
Кожна з цих кореляцій є кореляцією нульового порядку .
Додаткові ресурси
Наступні посібники надають додаткову інформацію про коефіцієнти кореляції:
Введення в коефіцієнт кореляції Пірсона
Як читати кореляційну матрицю
Як розрахувати часткову кореляцію в Excel