Середнє арифметичне

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

Тут ми пояснюємо, що таке середнє арифметичне і як воно обчислюється. Ви знайдете приклади середнього арифметичного значення та навіть калькулятор для визначення середнього арифметичного будь-якої статистичної вибірки. Нарешті, ви зможете побачити, які властивості має цей тип середнього і як середнє арифметичне отримується з даними, згрупованими в інтервали.

Що таке середнє арифметичне?

Середнє арифметичне є центральною характеристикою набору статистичних даних. Для обчислення середнього арифметичного всі значення складаються і діляться на загальну кількість даних.

Крім того, середнє арифметичне є одним із основних показників, що використовуються для статистичного дослідження вибірки.

Отже, формула середнього арифметичного має такий вигляд:

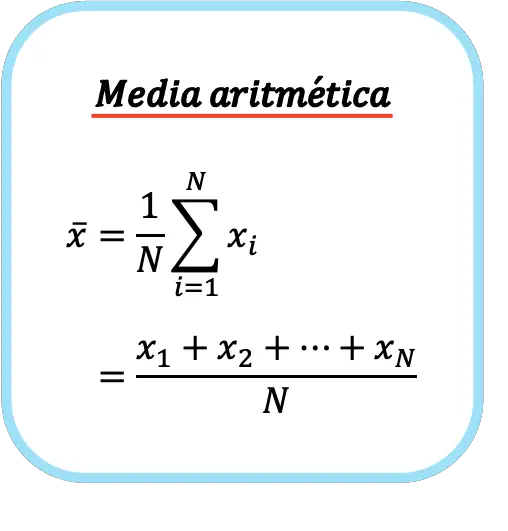
Символом середнього арифметичного є горизонтальна смуга над буквою х.

$(\overline{x}).$

Ви також можете відрізнити середнє значення вибірки від середнього сукупності за допомогою символу середнього: середнє значення вибірки виражається символом

$\overline{x}$

, з іншого боку, для середнього значення населення ми використовуємо грецьку літеру

$\mu.$

Слід зазначити, що середнє арифметичне сукупності еквівалентно очікуваному значенню статистичної змінної.

Середнє арифметичне, яке також називають середнім арифметичним, не є єдиним типом середнього, який існує, серед іншого існують також середнє зважене, середнє квадратичне, середнє геометричне та середнє гармонічне. Як розраховується кожен з них, ви можете побачити в пошуковій системі нашого сайту.

Як обчислити середнє арифметичне

Для обчислення середнього арифметичного необхідно виконати наступні дії:

Додайте всі статистичні дані з вибірки.
Поділіть попередню суму на загальну кількість даних.
Отриманий результат є середнім арифметичним статистичної вибірки.

👉 Ви можете скористатися калькулятором, наведеним нижче, щоб обчислити середнє арифметичне будь-якого набору даних.

Приклад обчислення середнього арифметичного

З огляду на визначення середнього арифметичного, ми побачимо, як отримати середнє арифметичне набору даних, розв’язуючи приклад крок за кроком.

За навчальний рік учень отримав такі оцінки: з математики – 9, з мови – 7, з історії – 6, з економіки – 8, з природознавства – 7,5. Яке середнє арифметичне всіх ваших оцінок?

Щоб знайти середнє арифметичне, потрібно скласти всі оцінки, а потім розділити на загальну кількість предметів у курсі, тобто 5. Тому застосовуємо формулу середнього арифметичного:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

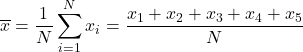
Підставляємо дані у формулу і обчислюємо середнє арифметичне:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Як бачимо, у середньому арифметичному кожному значенню присвоюється однакова вага, тобто кожна частина даних має однакову вагу в межах цілого.

Калькулятор середнього арифметичного

Введіть дані будь-якої статистичної вибірки в наступний калькулятор, щоб обчислити її середнє арифметичне. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Середнє арифметичне для згрупованих даних

Під згрупованими даними ми маємо на увазі, що дані структуровані як групи або інтервали. Зазвичай це відбувається, коли розмір статистичної вибірки дуже великий.

Отже, обчислення середнього арифметичного дещо змінюється, коли дані згруповані разом, навіть якщо концепція однакова.

Щоб обчислити середнє арифметичне даних, згрупованих в інтервали, оцінку класу кожної групи потрібно помножити на її абсолютну частоту, а потім розділити на суму всіх абсолютних частот.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Примітка. Оцінка класу інтервалу обчислюється шляхом ділення суми кінцевих точок інтервалу на два. Наприклад, нота класу інтервалу [3,7) буде такою:

$\cfrac{3+7}{2}=5$

Щоб ви могли побачити, як це робиться, нижче наведено розв’язану вправу на середнє арифметичне даних, згрупованих у інтервали:

Ми хочемо статистично вивчити вагу групи, для цього ми опитали репрезентативну групу з 81 людини та отримали такі дані:

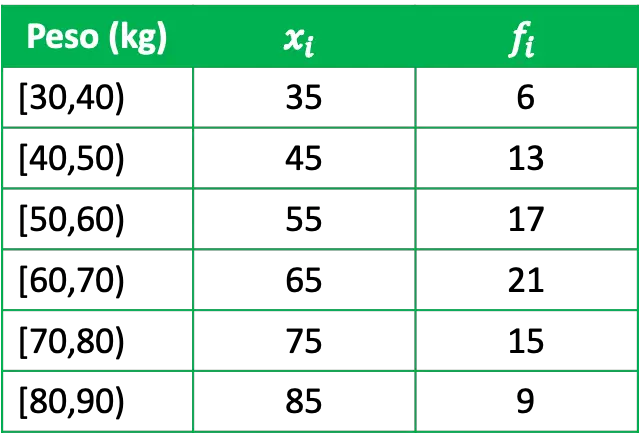
Де x _i — оцінка класу кожної групи, а f _{i —} її абсолютна частота, тобто кількість людей, які мають вагу в цьому інтервалі.

Щоб визначити середнє арифметичне, необхідно додати в таблицю частот стовпець, який є добутком нотаток класу на їх відповідні абсолютні частоти:

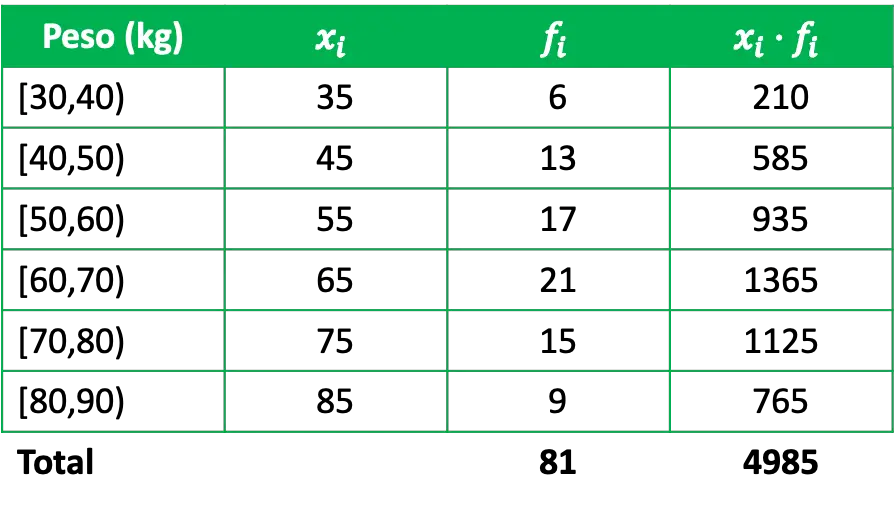
вправа на середнє арифметичне для згрупованих даних

Таким чином, щоб обчислити середнє арифметичне згрупованих даних, просто розділіть суму добутків нотаток класу на їх частоти на загальну кількість даних:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Властивості середнього арифметичного

Середнє арифметичне має такі характеристики:

Сума відхилень усіх даних у розподілі від середнього призводить до нуля.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Якщо ми додамо однакову кількість до всіх даних у вибірці, середнє значення вибірки збільшиться на цю кількість.

Те ж саме відбувається з множенням: якщо помножити всі значення у вибірці на число, вибіркове середнє множиться на це число.

Середнє арифметичне можна обчислити лише в кількісних змінних . Іншими словами, ви не можете взяти середнє значення якісних змінних.

Середнє арифметичне завжди буде значенням між мінімумом і максимумом розподілу.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Цей тип середнього значення дуже чутливий до дуже високих або дуже низьких значень, що призводить до того, що викид суттєво змінює результат середнього арифметичного.

Середнє арифметичне набору даних завжди дорівнює або перевищує середнє геометричне того самого набору даних.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Обчисліть середнє арифметичне за допомогою Excel

Розрахувати середнє арифметичне в Excel дуже просто, так як вам достатньо ввести дані на аркуші та скористатися функцією AVERAGE .

Наприклад, щоб визначити середнє арифметичне даних із першої розв’язаної вправи, яку ми пояснювали, просто скопіюйте всі дані в документ Excel і запишіть таку формулу в клітинку: =AVERAGE(9;7;5; 8;7) ,5) . Функція поверне середнє арифметичне даних, яке дорівнює 7,3.

Очевидно, що знайти середнє арифметичне певних чисел за допомогою програми Excel набагато швидше, ніж обчислювати його вручну, особливо коли розмір вибірки дуже великий.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше