Лінійний дискримінантний аналіз в r (крок за кроком)

Лінійний дискримінантний аналіз — це метод, який можна використовувати, якщо у вас є набір змінних-прогнозів і ви хочете класифікувати змінну відповіді на два або більше класів.

Цей підручник надає покроковий приклад того, як виконувати лінійний дискримінантний аналіз у R.

Крок 1: Завантажте необхідні бібліотеки

Спочатку ми завантажимо необхідні бібліотеки для цього прикладу:

 library (MASS)
library (ggplot2)

Крок 2: Завантажте дані

У цьому прикладі ми будемо використовувати набір даних райдужної оболонки ока, вбудований у R. Наступний код показує, як завантажити та відобразити цей набір даних:

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Ми бачимо, що набір даних містить 5 змінних і загалом 150 спостережень.

Для цього прикладу ми створимо модель лінійного дискримінантного аналізу, щоб класифікувати, до якого виду належить дана квітка.

У моделі ми будемо використовувати наступні змінні предиктора:

• Чашолисток.довж
• Чашолисток.Шир
• Пелюстка. Довжина
• Пелюстка. Ширина

І ми використаємо їх, щоб передбачити змінну відповіді Species , яка підтримує такі три потенційні класи:

• сетоза
• лишай
• Вірджинія

Крок 3: масштабуйте дані

Одним із ключових припущень лінійного дискримінантного аналізу є те, що кожна зі змінних предикторів має однакову дисперсію. Простий спосіб переконатися, що це припущення виконується, полягає в масштабуванні кожної змінної так, щоб вона мала середнє значення 0 і стандартне відхилення 1.

Ми можемо зробити це швидко в R за допомогою функції scale() :

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

Ми можемо використати функцію apply() , щоб переконатися, що кожна змінна предиктора тепер має середнє значення 0 і стандартне відхилення 1:

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

Крок 4: Створення навчальних і тестових зразків

Далі ми розділимо набір даних на навчальний набір для навчання моделі та тестовий набір для перевірки моделі:

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Крок 5: Налаштуйте модель LDA

Далі ми використаємо функцію lda() з пакету MASS , щоб адаптувати модель LDA до наших даних:

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

Ось як інтерпретувати результати моделі:

Групові попередні ймовірності: вони представляють пропорції кожного виду в навчальному наборі. Наприклад, 35,8% усіх спостережень у навчальному наборі були для виду virginica .

Середні значення групи: вони відображають середні значення кожної змінної предиктора для кожного виду.

Лінійні дискримінантні коефіцієнти: вони відображають лінійну комбінацію змінних предикторів, які використовуються для навчання правила прийняття рішень моделі LDA. Наприклад:

• LD1: 0,792 * довжина чашолистка + 0,571 * ширина чашолистка – 4,076 * довжина пелюстки – 2,06 * ширина пелюстки
• LD2: 0,529 * довжина чашолистка + 0,713 * ширина чашолистка – 2,731 * довжина пелюстки + 2,63 * ширина пелюстки

Пропорція трасування: відображає відсоток поділу, досягнутий кожною лінійною дискримінантною функцією.

Крок 6. Використовуйте модель для прогнозування

Після того, як ми підібрали модель, використовуючи наші навчальні дані, ми можемо використовувати її для прогнозування наших тестових даних:

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

Це повертає список із трьома змінними:

• клас: прогнозований клас
• posterior: апостеріорна ймовірність того, що спостереження належить до кожного класу
• x: Лінійні дискримінанти

Ми можемо швидко візуалізувати кожен із цих результатів для перших шести спостережень у нашому тестовому наборі даних:

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

Ми можемо використати наступний код, щоб побачити, для якого відсотка спостережень модель LDA правильно передбачила вид:

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Виявилося, що модель правильно передбачила вид для 100% спостережень у нашому тестовому наборі даних.

У реальному світі модель LDA рідко правильно прогнозує результати кожного класу, але цей набір даних райдужної оболонки просто побудований таким чином, що алгоритми машинного навчання, як правило, працюють дуже добре.

Крок 7: Візуалізуйте результати

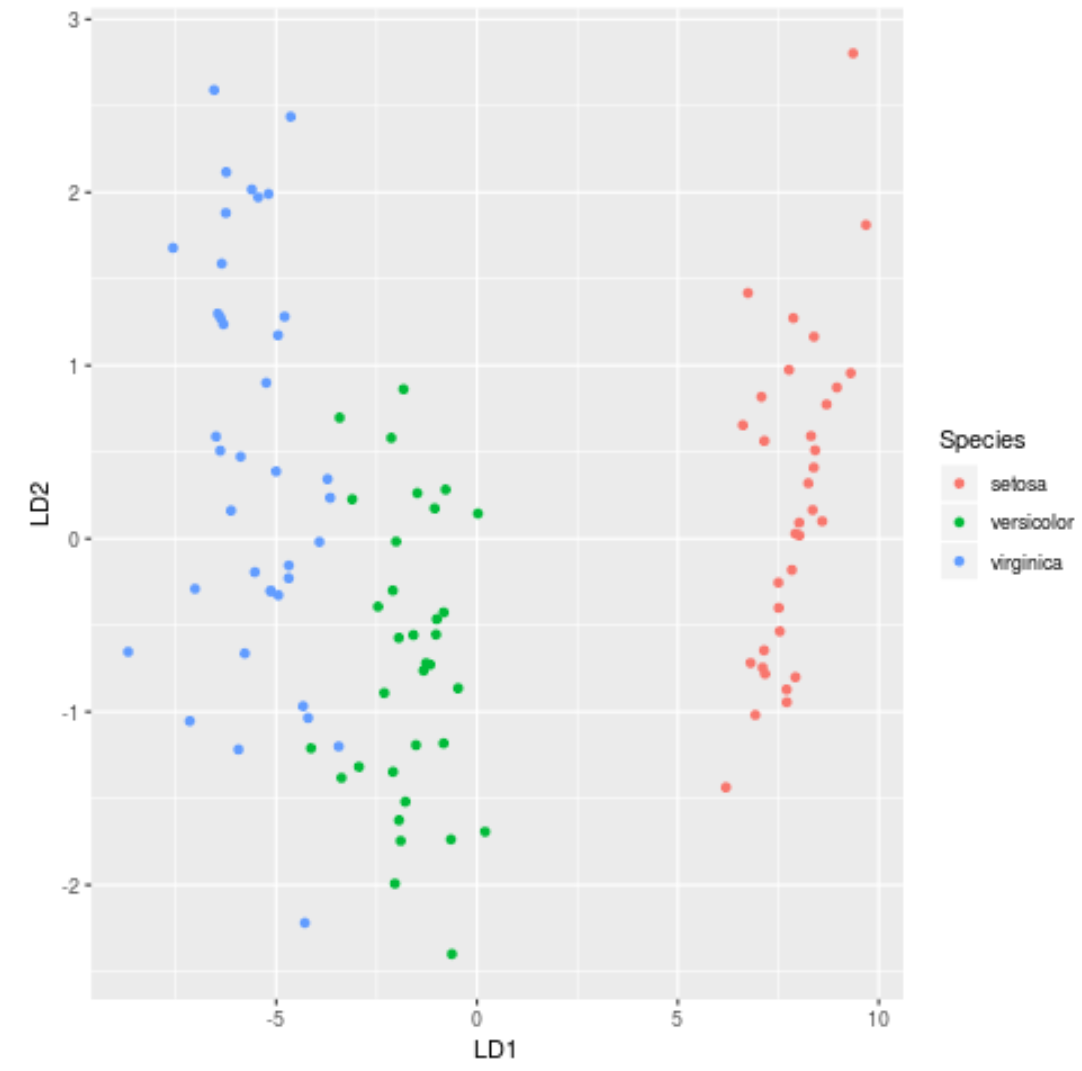
Нарешті, ми можемо створити графік LDA, щоб візуалізувати лінійні дискримінанти моделі та візуалізувати, наскільки добре вона розділяє три різні види в нашому наборі даних:

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

Ви можете знайти повний код R, використаний у цьому посібнику, тут .