Середні типи (статистика)

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

Тут ми пояснюємо, що таке всі типи середніх значень у статистиці та як вони обчислюються. Ви знайдете формулу для кожного типу панчіх і приклади.

Але перш ніж побачити, що таке середнє значення, ми повинні логічно знати, що таке середнє в статистиці. Тому ми рекомендуємо вам переглянути наступне посилання, перш ніж продовжити.

➤ Дивіться: Що таке середнє (статистика)?

Які існують види середніх величин у статистиці?

У статистиці існують такі види середніх величин:

Середнє арифметичне
Середнє зважене
Геометричні засоби
корінь означає квадрат
гармонійне значення
узагальнена середня
узагальнене f-середнє
обрізані засоби
інтерквартильне середнє
середнє значення функції

Далі ми пояснимо, як обчислювати всі типи середніх у статистиці. П’ять найбільш часто використовуваних типів середнього – це середнє арифметичне, середнє зважене, середнє геометричне, середнє квадратичне та середнє гармонічне. Тож ми збираємося детальніше зупинитися на цих п’яти основних типах медіа.

Середнє арифметичне

Середнє арифметичне обчислюється шляхом додавання всіх значень і подальшого ділення на загальну кількість точок даних.

Отже, формула середнього арифметичного має такий вигляд:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

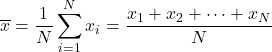
Середнє арифметичне також відоме як середнє арифметичне .

Середнє арифметичне, ймовірно, найбільш використовуваний тип середнього в статистиці.

Щоб побачити приклад отримання цього типу середнього значення, ми обчислимо середнє арифметичне таких даних:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Щоб обчислити середнє арифметичне, просто скласти всі статистичні дані та розділити на загальну кількість даних, яка дорівнює 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Середнє зважене

Щоб обчислити середньозважену величину, ви повинні спочатку помножити кожну статистичну інформацію на її вагу (або вагу), потім додати всі продукти й, нарешті, розділити зважену суму на суму всіх ваг.

Таким чином, формула середньозваженого значення виглядає так:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

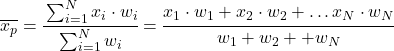
Де x _i — статистичне значення, а w _{i —} його відповідна вага.

Середнє зважене важче зрозуміти, тому ми рекомендуємо переглянути наступний приклад, у якому крок за кроком пояснюється, як воно обчислюється:

➤ Див.: Приклад середньозваженого

Геометричні засоби

Середнє геометричне набору статистичних даних дорівнює кореню n-ої частини з добутку всіх значень.

Цей тип середнього значення використовується в бізнес-фінансах для розрахунку норми прибутку, середніх відсотків і складних відсотків.

Формула такого типу зберігання досить складна. Насправді середнє геометричне для всіх статистичних наборів не можна обчислити, але іноді цей тип середнього неможливо визначити. Ось чому ми рекомендуємо ознайомитися з усіма винятками, поясненими за цим посиланням:

➤ Див.: формула середнього геометричного

корінь означає квадрат

Середнє квадратичне значення дорівнює квадратному кореню із середнього арифметичного з квадратів даних.

Тому формула середнього квадрата має такий вигляд:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Цей тип середнього значення також називають середньоквадратичним , середньоквадратичним або RMS .

Відзначимо лише, що кубічне середнє також існує, але воно використовується в дуже особливих випадках.

Квадратне усереднення має переваги та недоліки, наприклад, воно особливо корисне, коли статистична змінна приймає додатні та від’ємні значення, оскільки, зводячи кожен фрагмент даних у квадрат, усі значення стають додатними. Ви можете побачити більше функцій цього типу медіа, натиснувши це посилання:

➤ Дивіться: переваги та недоліки середнього квадратичного кореня

гармонійне значення

Середнє гармонійне обчислюється шляхом ділення загальної кількості статистичних даних на суму зворотних величин кожного значення.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

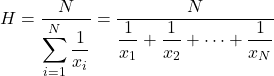
Гармонічне середнє використовується для обчислення середніх швидкостей, часу або проведення електронних розрахунків. Ця характеристика відрізняє гармонічне середнє від інших типів середніх, які часто використовуються при розрахунку середніх цін або відсотків.

Ви можете побачити приклади обчислення цього типу середнього значення на наступній сторінці:

➤ Див.: приклади гармонічного значення

Інші види панчіх

У цьому розділі ми побачимо формули для інших типів панчіх. Ми не будемо вдаватися в подробиці кожного типу, оскільки вони не є широко поширеними, але вам корисно знати, що існують інші типи панчіх.

Узагальнене середнє є сумішшю середніх типів, розглянутих вище, і обчислюється за такою формулою:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

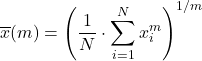
Нехай f — ін’єктивна та монотонна функція, тоді узагальнене f-середнє визначається як:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

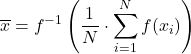
Урізане середнє передбачає обчислення середнього арифметичного після віднімання відсотка спостережень у верхньому та нижньому кінцях вибірки. З обох кінців має бути відхилений однаковий відсоток.

Щоб обчислити міжквартильне середнє , яке також називається міжквартильним середнім, спочатку відкидаються дані з першого та четвертого квартилів, а потім обчислюється середнє арифметичне лише другого та третього квартилів вибірки. Таким чином, формула для цього типу середнього значення:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

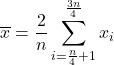
Нарешті, ви також можете знайти середнє значення функції . Середнє значення неперервної функції на замкнутому інтервалі [a,b] обчислюється за формулою:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Середнє значення вибірки та сукупності

Нарешті, ми побачимо, яка різниця між середнім значенням вибірки та середнім показником сукупності, двома типами середніх значень, які часто плутають.

Вибіркове середнє – це середнє, обчислене за значеннями статистичної вибірки, тобто воно обчислюється за частиною всіх значень змінної.

Середня сукупність – це середня величина, обчислена для статистичної сукупності, тобто для всіх значень змінної. Отже, середнє сукупності збігається з математичним сподіванням змінної.

Вибіркове середнє можна вважати практично рівним середньому сукупності, якщо відома достатньо велика кількість даних. Але значення середньої сукупності дуже важко отримати, оскільки насправді всі значення розподілу рідко відомі.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше