Вступ до поліноміальної регресії
Коли у нас є набір даних зі змінною-прогнозатором і змінною відповіді , ми часто використовуємо просту лінійну регресію для кількісного визначення зв’язку між двома змінними.
Однак проста лінійна регресія (SLR) передбачає, що зв’язок між предиктором і змінною відповіді є лінійним. Записаний у математичній нотації, SLR припускає, що зв’язок має вигляд:
Y = β 0 + β 1 X + ε
Але на практиці зв’язок між двома змінними насправді може бути нелінійним, і спроба використати лінійну регресію може призвести до погано відповідної моделі.
Одним із способів врахування нелінійного зв’язку між предиктором і змінною відповіді є використання поліноміальної регресії , яка набуває вигляду:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
У цьому рівнянні h називається ступенем полінома.
Коли ми збільшуємо значення h , модель здатна краще враховувати нелінійні зв’язки, але на практиці ми рідко вибираємо значення h , яке перевищує 3 або 4. Поза цим показником модель стає надто гнучкою та переповнює дані .
Технічні примітки
- Хоча поліноміальна регресія може відповідати нелінійним даним, вона все ще вважається формою лінійної регресії, оскільки вона є лінійною за коефіцієнтами β1 , β2 , …, βh .
- Поліноміальну регресію також можна використовувати для кількох змінних предикторів, але це створює умови взаємодії в моделі, що може зробити модель надзвичайно складною, якщо використовується кілька змінних предикторів.
Коли використовувати поліноміальну регресію
Ми використовуємо поліноміальну регресію, коли зв’язок між предиктором і змінною відповіді є нелінійним.
Існує три поширених способи виявлення нелінійного зв’язку:
1. Створіть діаграму розсіювання.
Найпростіший спосіб виявити нелінійний зв’язок – створити діаграму розсіювання змінної відповіді проти змінної предиктора.
Наприклад, якщо ми створимо наступну діаграму розсіювання, ми побачимо, що зв’язок між двома змінними є приблизно лінійним, тому проста лінійна регресія, ймовірно, добре працюватиме з цими даними.
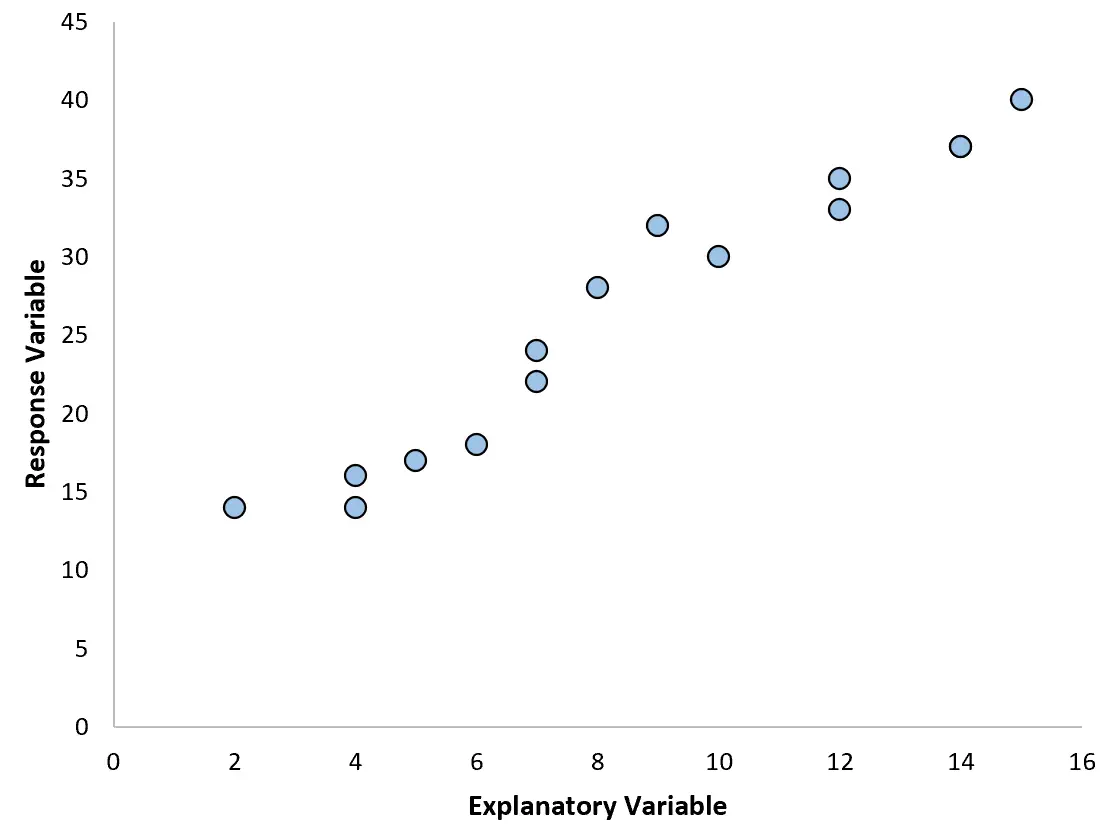
Однак, якщо наша діаграма розсіювання виглядає як один із наведених нижче графіків, ми можемо побачити, що залежність є нелінійною, і тому поліноміальна регресія буде хорошою ідеєю:
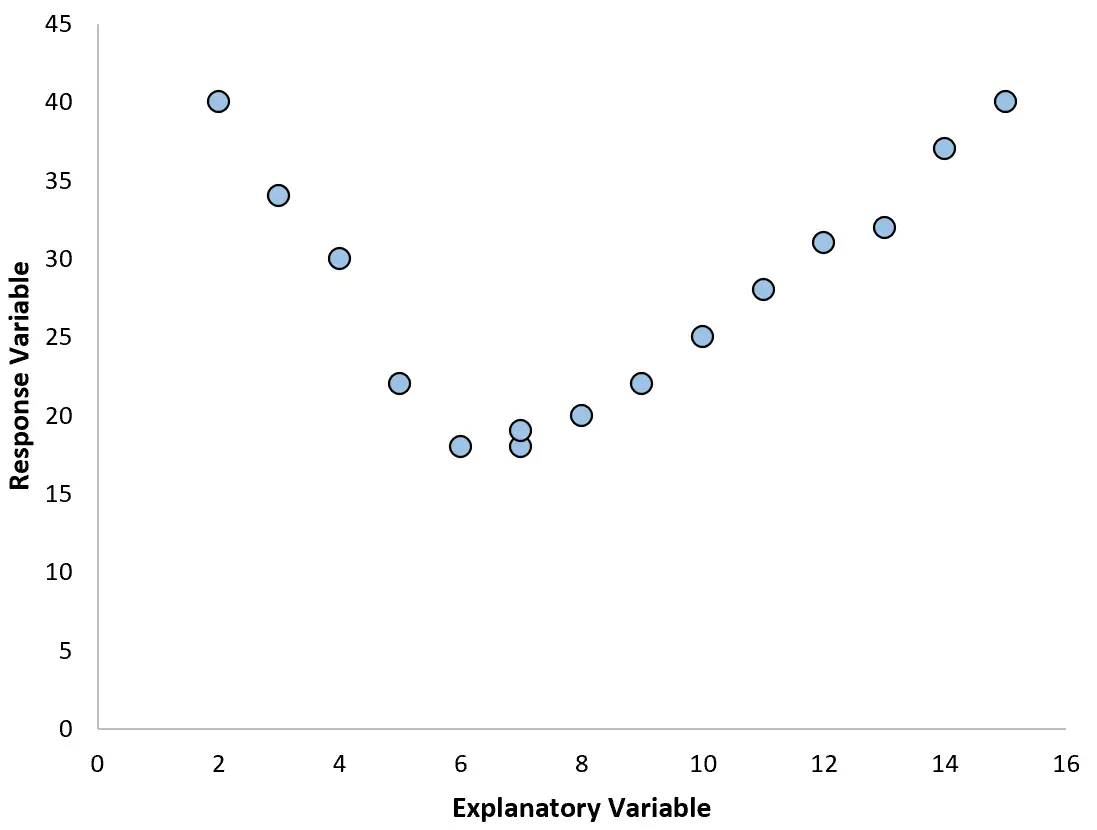
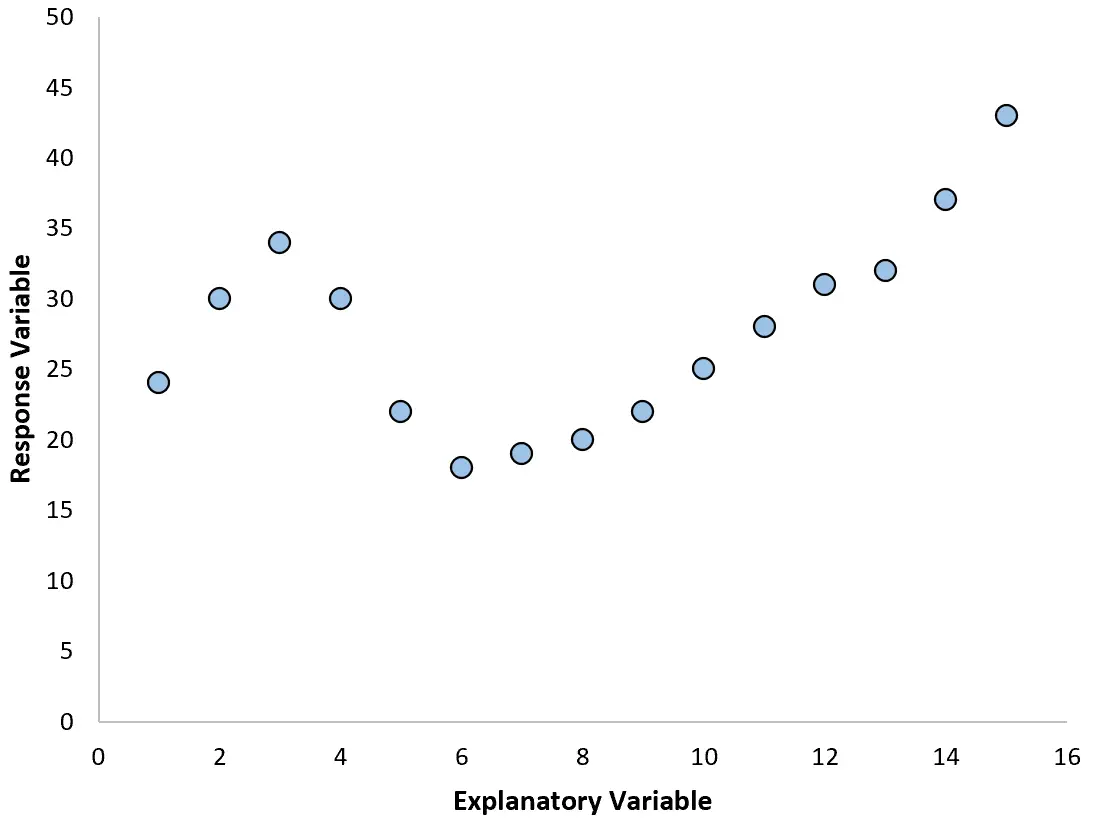
2. Створіть графік залишків проти підігнаного графіка.
Інший спосіб виявити нелінійність полягає в тому, щоб підібрати просту модель лінійної регресії до даних, а потім побудувати графік залишків від підігнаних значень .
Якщо залишки на графіку розподілені приблизно рівномірно навколо нуля без чіткої тенденції, тоді простої лінійної регресії, ймовірно, достатньо.
Однак, якщо залишки показують нелінійну тенденцію на графіку, це означає, що зв’язок між предиктором і відповіддю, ймовірно, нелінійний.
3. Розрахувати R 2 моделі.
Значення R 2 регресійної моделі повідомляє вам про відсоток варіації змінної відповіді, який можна пояснити змінною(ями) предиктора.
Якщо ви підбираєте просту модель лінійної регресії до набору даних і значення R 2 моделі є досить низьким, це може означати, що зв’язок між предиктором і змінною відповіді складніший, ніж простий лінійний зв’язок.
Це може бути ознакою того, що вам, можливо, доведеться замість цього спробувати поліноміальну регресію.
За темою: що таке хороше значення R-квадрат?
Як вибрати ступінь многочлена
Модель поліноміальної регресії має такий вигляд:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
У цьому рівнянні h є ступенем полінома.
Але як вибрати значення для h ?
На практиці ми підбираємо кілька різних моделей з різними значеннями h і виконуємо k-кратну перехресну перевірку , щоб визначити, яка модель дає найменшу тестову середньоквадратичну помилку (MSE).
Наприклад, ми можемо підібрати такі моделі до заданого набору даних:
- Y = β 0 + β 1
- Y = β 0 + β 1 X + β 2 X 2
- Y = β0 + β1X + β2X2 + β3X3
- Y = β 0 + β 1 X + β 2 X 2 + β 3 X 3 + β 4 X 4
Потім ми можемо використати k-кратну перехресну перевірку, щоб обчислити тест MSE для кожної моделі, який покаже нам, наскільки добре кожна модель працює на даних, яких вона ніколи раніше не бачила.
Компроміс зміщення-дисперсії поліноміальної регресії
Під час використання поліноміальної регресії існує компроміс зміщення-дисперсії . Коли ми збільшуємо ступінь полінома, зсув зменшується (оскільки модель стає більш гнучкою), але дисперсія збільшується.
Як і з усіма моделями машинного навчання, нам потрібно знайти оптимальний компроміс між зміщенням і дисперсією.
У більшості випадків це дозволяє певною мірою підвищити ступінь полінома, але за межами певного значення модель починає адаптуватися до шуму в даних, і MSE тесту починає зменшуватися.
Щоб переконатися, що модель є гнучкою, але не надто гнучкою, ми використовуємо k-кратну перехресну перевірку, щоб знайти модель, яка дає найнижчий тест MSE.
Як виконати поліноміальну регресію
У наступних посібниках наведено приклади виконання поліноміальної регресії в різному програмному забезпеченні:
Як виконати поліноміальну регресію в Excel
Як виконати поліноміальну регресію в R
Як виконати поліноміальну регресію в Python
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше