Як створити випадкові ліси в r (крок за кроком)

Коли зв’язок між набором змінних предиктора та змінною відповіді дуже складний, ми часто використовуємо нелінійні методи для моделювання зв’язку між ними.

Одним із таких методів є побудова дерева рішень . Однак недоліком використання єдиного дерева рішень є те, що воно часто страждає від великої дисперсії .

Тобто, якщо ми розділимо набір даних на дві половини та застосуємо дерево рішень до обох половин, результати можуть бути дуже різними.

Одним із методів, який ми можемо використати для зменшення дисперсії окремого дерева рішень, є побудова моделі випадкового лісу , яка працює наступним чином:

1. Візьміть b початкових зразків із вихідного набору даних.

2. Створіть дерево рішень для кожного зразка початкового завантаження.

• При побудові дерева кожного разу, коли розглядається розбиття, лише випадкова вибірка з m предикторів вважається кандидатами на розщеплення з повного набору p предикторів. Зазвичай ми вибираємо m рівним √p .

3. Усередніть прогнози з кожного дерева, щоб отримати остаточну модель.

Виявляється, випадкові ліси, як правило, створюють набагато точніші моделі, ніж окремі дерева рішень і навіть пакетні моделі .

Цей підручник надає покроковий приклад того, як створити модель випадкового лісу для набору даних у R.

Крок 1: Завантажте необхідні пакети

Спочатку ми завантажимо необхідні пакети для цього прикладу. Для цього простого прикладу нам потрібен лише один пакет:

 library (randomForest)

Крок 2: Налаштуйте модель випадкового лісу

Для цього прикладу ми використаємо вбудований набір даних R під назвою Air Quality , який містить вимірювання якості повітря в Нью-Йорку протягом 153 окремих днів.

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

Цей набір даних містить 42 рядки з відсутніми значеннями. Тому перед підгонкою моделі випадкового лісу ми заповнимо відсутні значення в кожному стовпці медіанами стовпців:

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

Пов’язане: Як призначити відсутні значення в R

У наведеному нижче коді показано, як підігнати модель випадкового лісу в R за допомогою функції randomForest() із пакета randomForest .

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

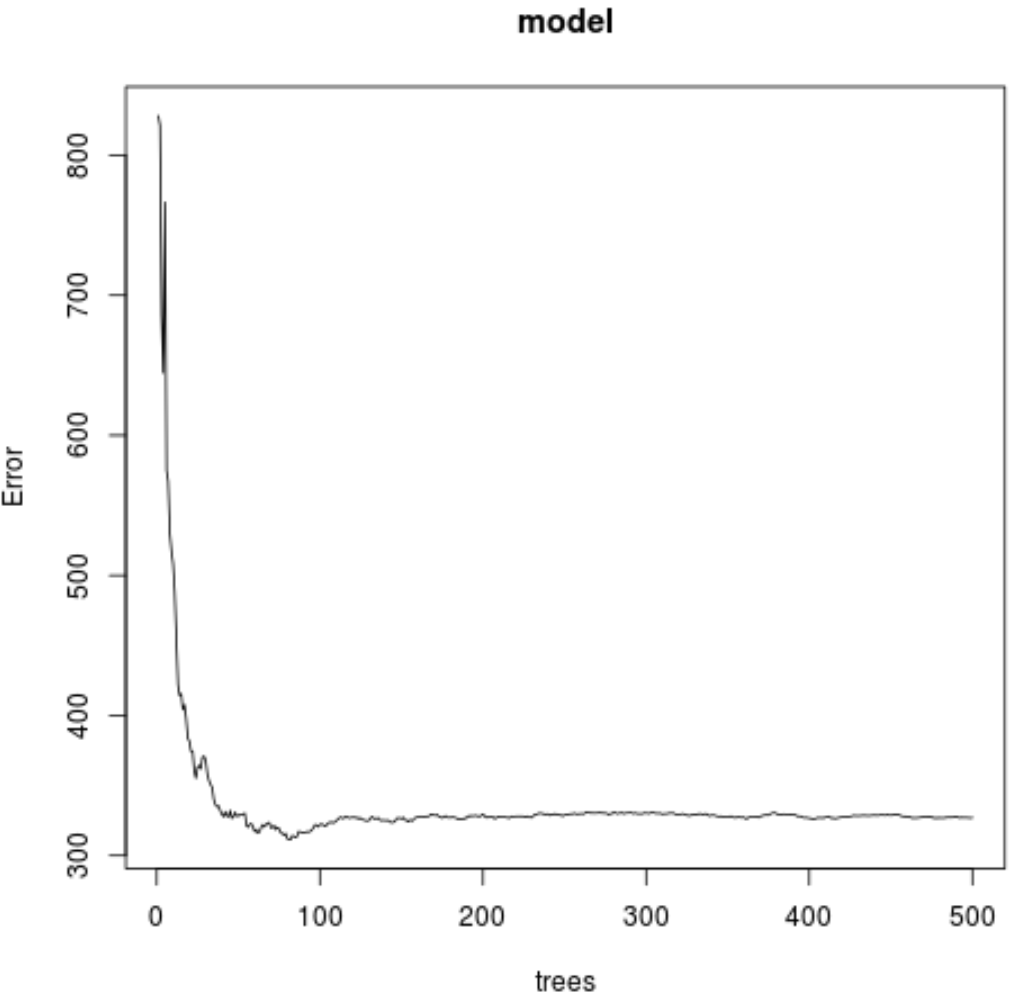
З результату ми бачимо, що модель, яка дала найменшу середню квадратичну помилку (MSE), використовувала 82 дерева.

Ми також бачимо, що середня квадратична помилка цієї моделі становила 17,64392 . Ми можемо розглядати це як середню різницю між прогнозованим значенням озону та фактичним спостережуваним значенням.

Ми також можемо використати наступний код, щоб побудувати графік тесту MSE на основі кількості використаних дерев:

 #plot the MSE test by number of trees
plot(model)

І ми можемо використовувати функцію varImpPlot() , щоб створити графік, який відображає важливість кожної змінної предиктора в кінцевій моделі:

 #produce variable importance plot
varImpPlot(model) 

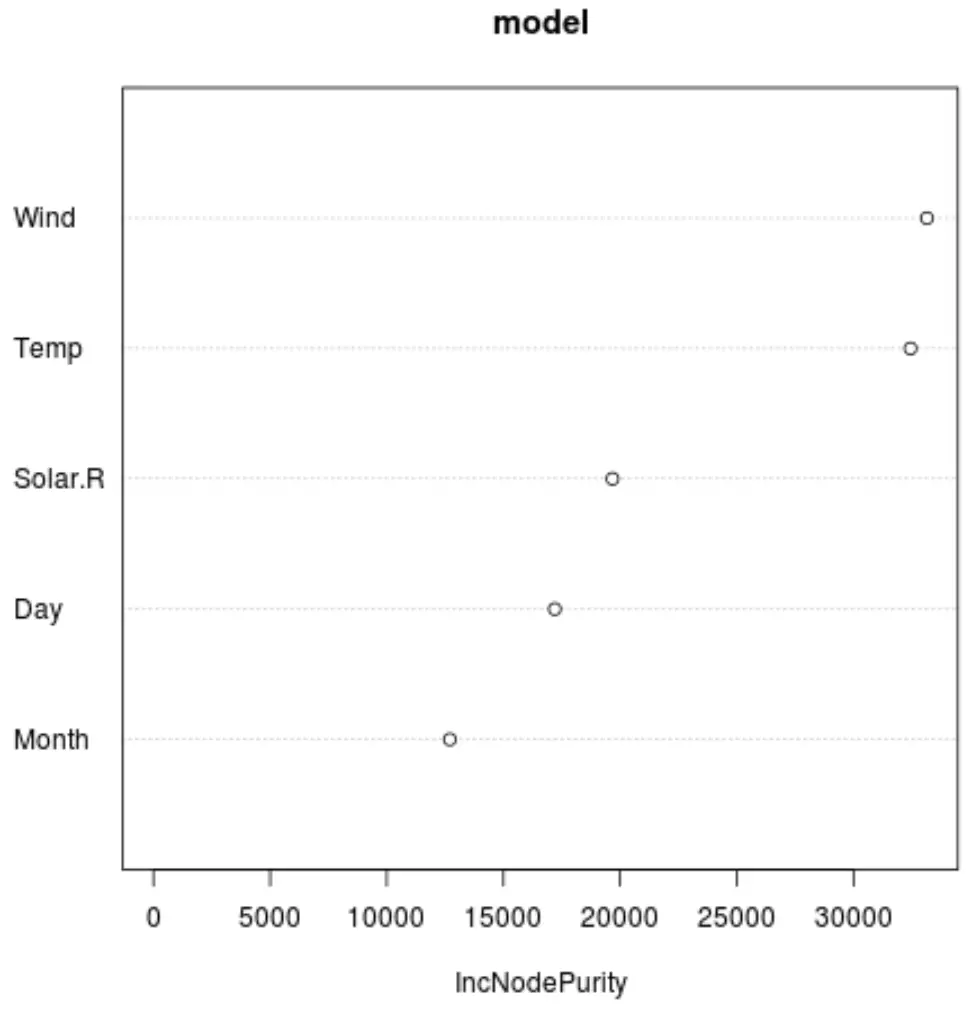
Вісь X відображає середнє збільшення чистоти вузлів дерев регресії як функцію розподілу між різними предикторами, відображеними на осі Y.

З графіка ми бачимо, що вітер є найважливішою змінною прогностикою, за якою слідує температура .

Крок 3: Налаштуйте модель

За замовчуванням функція randomForest() використовує 500 дерев і (загальна кількість предикторів/3) випадково вибраних предикторів як потенційних кандидатів для кожного розбиття. Ми можемо налаштувати ці параметри за допомогою функції tuneRF() .

У наведеному нижче коді показано, як знайти оптимальну модель за такими специфікаціями:

• ntreeTry: кількість дерев для побудови.
• mtryStart: початкова кількість змінних предикторів, які слід враховувати при кожному діленні.
• StepFactor: Коефіцієнт, який потрібно збільшувати, доки оцінена помилка «поза пакета» не перестане покращуватися на певну величину.
• покращити: величина, на яку має бути покращена помилка виходу з сумки, щоб продовжувати збільшувати коефіцієнт кроку.

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

Ця функція створює наступний графік, на якому відображається кількість предикторів, що використовуються для кожного розбиття під час побудови дерев на осі х, і оцінена помилка поза мішком на осі у:

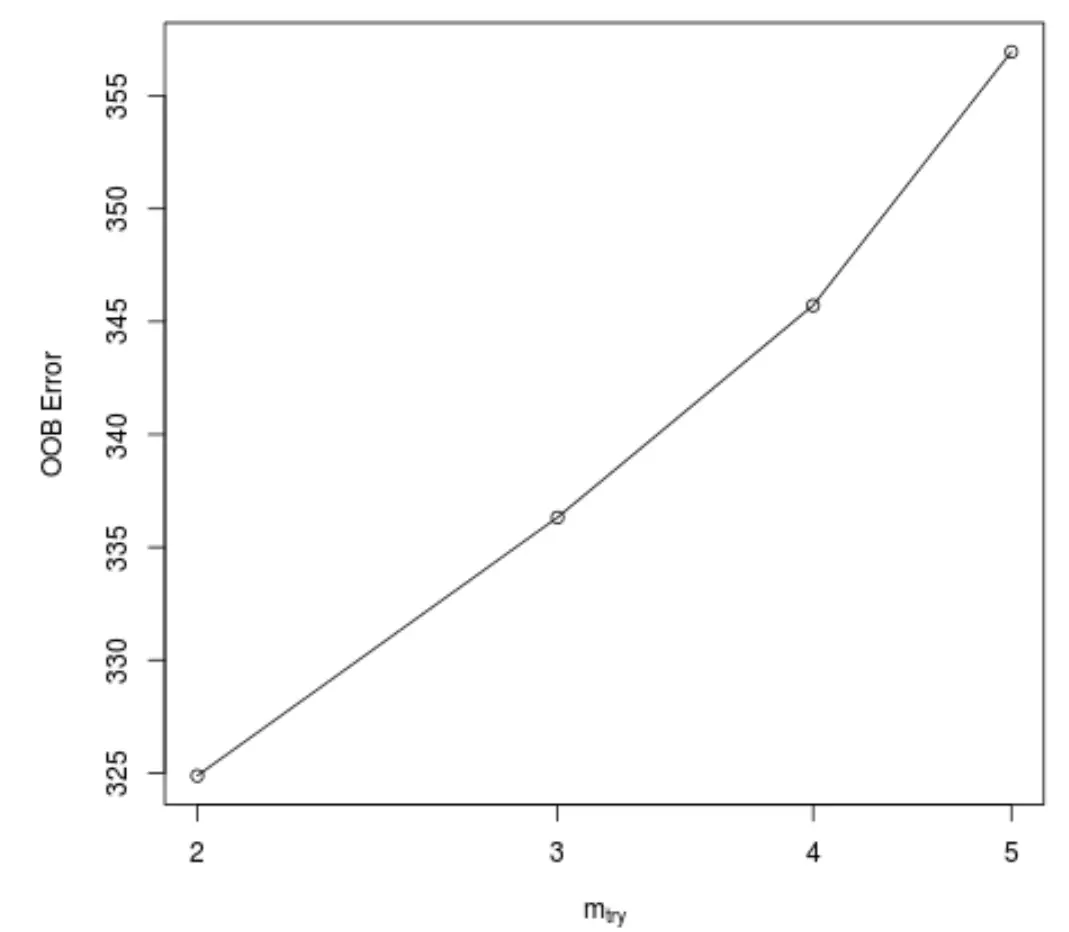
Ми бачимо, що найменша помилка OOB отримана за допомогою використання 2 випадково вибраних предикторів при кожному розділенні під час побудови дерев.

Це фактично відповідає налаштуванню за замовчуванням (загальна кількість предикторів/3 = 6/3 = 2), яке використовується початковою функцією randomForest() .

Крок 4. Використовуйте остаточну модель для прогнозування

Нарешті, ми можемо використовувати скориговану модель випадкового лісу, щоб робити прогнози щодо нових спостережень.

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

Ґрунтуючись на значеннях прогностичних змінних, встановлена модель випадкового лісу передбачає, що значення озону становитиме 27,19442 у цей конкретний день.

Повний код R, використаний у цьому прикладі, можна знайти тут .