Нормальний розподіл і t-розподіл: у чому різниця?

Нормальний розподіл є найбільш часто використовуваним розподілом у всій статистиці та відомий як симетричний і дзвоноподібний.

Тісно пов’язаним розподілом є t-розподіл , який також є симетричним і дзвоноподібним, але має важчі «хвости», ніж звичайний розподіл.

Іншими словами, більше значень у розподілі розташовано на кінцях, ніж у центрі порівняно з нормальним розподілом:

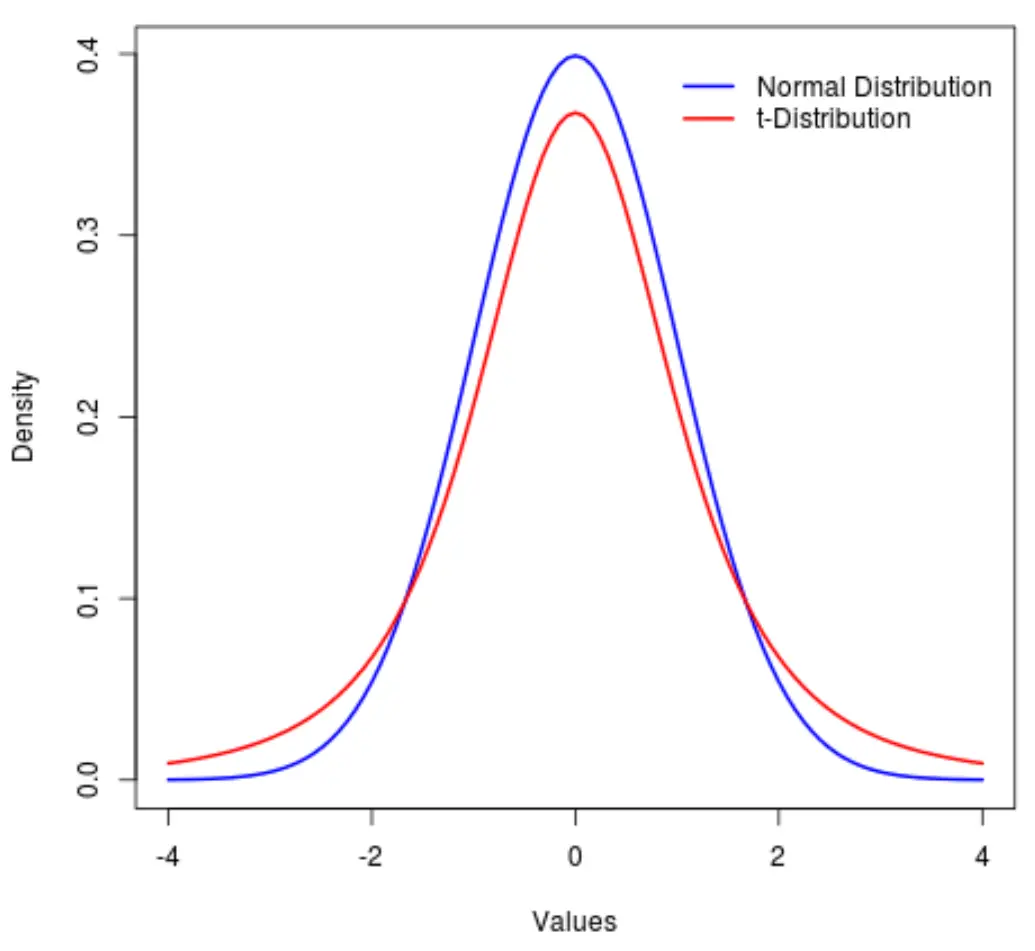
На статистичному жаргоні ми використовуємо показник, який називається ексцесом , щоб визначити, наскільки «важким» є розподіл. Отже, ми б сказали, що ексцес t-розподілу більший, ніж нормальний розподіл.

На практиці ми найчастіше використовуємо t-розподіл, коли виконуємо перевірку гіпотез або будуємо довірчі інтервали .

Наприклад, формула для обчислення довірчого інтервалу для середнього сукупності має вигляд:

Довірчий інтервал = x +/- t _{1-α/2, n-1} *(s/√ n )

золото:

• x : вибірка середніх
• t: критичне значення t, засноване на рівні значущості α та розмірі вибірки n
• s: вибіркове стандартне відхилення
• n: розмір вибірки

У цій формулі ми використовуємо критичне значення таблиці t замість критичного значення таблиці z, якщо виконується одна з таких умов:

• Ми не знаємо стандартне відхилення популяції.
• Розмір вибірки менше або дорівнює 30.

Наступна блок-схема надає корисний спосіб дізнатися, чи слід використовувати критичне значення з таблиці t чи таблиці z:

Основна відмінність між використанням t-розподілу та використанням нормального розподілу при побудові довірчих інтервалів полягає в тому, що критичні значення t-розподілу будуть більшими, що призводить до більш широких довірчих інтервалів.

Наприклад, припустімо, що ми хочемо побудувати 95% довірчий інтервал для середньої ваги популяції черепах, щоб зібрати випадкову вибірку черепах із такою інформацією:

• Обсяг вибірки n = 25
• Середня маса зразка х = 300
• Стандартне відхилення вибірки s = 18,5

Критичне значення z для 95% рівня довірчої вірогідності становить 1,96 , а критичне значення t для 95% довірчого інтервалу з df = 25-1 = 24 ступені свободи становить 2,0639 .

Таким чином, 95% довірчий інтервал для середнього значення сукупності з використанням z-критичного значення становить:

95% ДІ = 300 +/- 1,96*(18,5/√ 25 ) = [292,75, 307,25]

У той час як 95% довірчий інтервал для генеральної сукупності означає використання t-критичного значення:

95% ДІ = 300 +/- 2,0639*(18,5/√25) = [292,36, 307,64]

Зверніть увагу, що довірчий інтервал із t-критичним значенням ширший.

Ідея тут полягає в тому, що коли ми маємо невеликі розміри вибірки, ми менш впевнені щодо справжнього середнього значення сукупності, тому корисно використовувати t-розподіл для створення ширших довірчих інтервалів, які мають більше шансів утримувати справжнє середнє значення сукупності.

Візуалізація ступенів свободи t-розподілу

Слід зазначити, що зі збільшенням ступенів свободи розподіл t наближається до нормального розподілу.

Щоб проілюструвати це, розглянемо наступний графік, який показує форму t-розподілу з такими ступенями свободи:

• df = 3
• df = 10
• df = 30

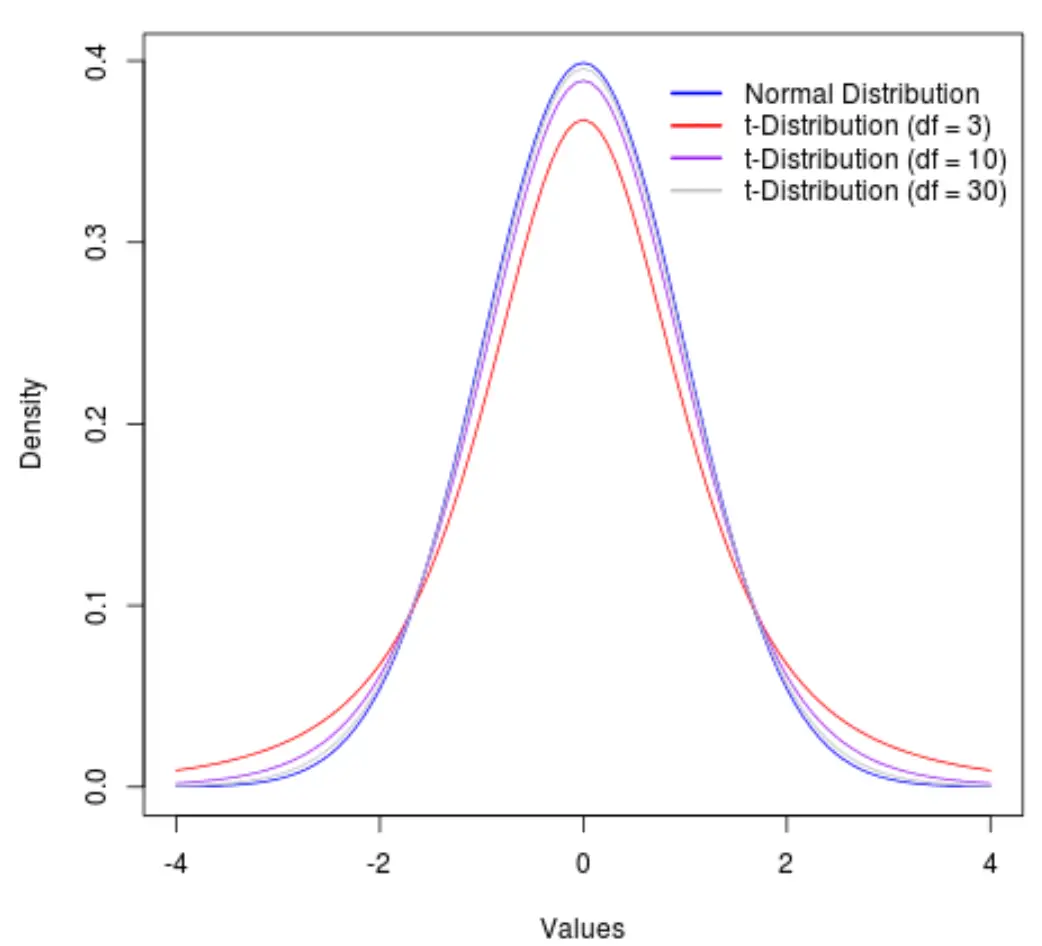
За межами 30 ступенів свободи t-розподіл і нормальний розподіл стають настільки схожими, що відмінності між використанням t-критичного значення та z-критичного значення у формулах стають незначними.