Stdev.p проти stdev.s в excel: у чому різниця?

Для обчислення стандартного відхилення в Excel можна використовувати три різні функції:

1. STDEV.P: Ця функція обчислює стандартне відхилення сукупності. Використовуйте цю функцію, коли діапазон значень представляє всю сукупність.

Ця функція використовує таку формулу:

Стандартне відхилення сукупності = √Σ (x _i – μ) ² / N

золото:

• Σ: грецький символ, що означає «сума»
• x _i : ^i-те значення набору даних
• μ: середня кількість населення
• N: Загальна кількість спостережень

2. STDEV.S: Ця функція обчислює стандартне відхилення вибірки. Використовуйте цю функцію, коли діапазон значень представляє вибірку значень, а не всю сукупність.

Ця функція використовує таку формулу:

Стандартне відхилення вибірки = √Σ (x _i – x ) ² / (n-1)

золото:

• Σ: грецький символ, що означає «сума»
• x _i : ^i-те значення набору даних
• x : вибірка означає
• N: Загальна кількість спостережень

3. STDEV: ця функція також обчислює стандартне відхилення вибірки. Вона поверне те саме значення, що й функція STDEV.S .

Технічна примітка:

Оскільки формула стандартного відхилення сукупності ділиться на N замість n-1 , стандартне відхилення сукупності завжди буде меншим за стандартне відхилення вибірки.

Причина, по якій стандартне відхилення сукупності буде меншим, полягає в тому, що якщо ми знаємо кожне значення генеральної сукупності, ми знаємо точне стандартне відхилення.

Однак, коли ми маємо лише вибірку сукупності, ми маємо більше невизначеності щодо точного стандартного відхилення загальної сукупності, тому наша оцінка стандартного відхилення має бути більшою.

У наступному прикладі показано, як використовувати ці функції на практиці.

Приклад: STDEV.P проти STDEV.S в Excel

Припустимо, що в Excel є такий набір даних:

На наступному знімку екрана показано, як обчислити стандартне відхилення набору даних за допомогою трьох різних формул стандартного відхилення:

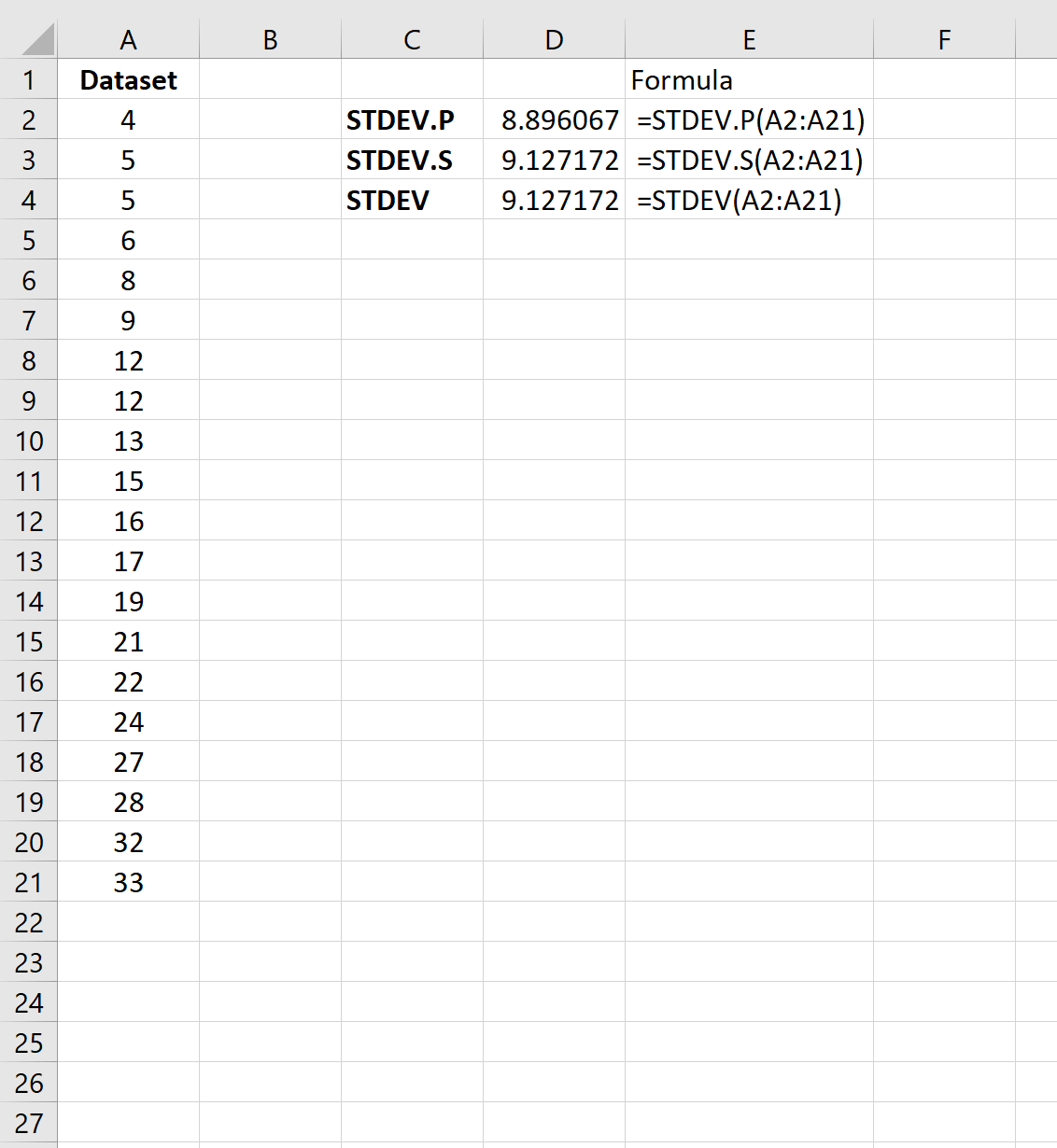
Стандартне відхилення вибірки виявляється 9,127 , а стандартне відхилення сукупності – 8,896 .

Як згадувалося раніше, стандартне відхилення генеральної сукупності завжди буде меншим за стандартне відхилення вибірки.

Коли використовувати STDEV.P проти STDEV.S

У більшості випадків ми не можемо зібрати дані для всієї сукупності. Тому ми збираємо дані лише для вибірки населення.

Отже, ми майже завжди використовуємо STDEV.S для обчислення стандартного відхилення набору даних, оскільки наш набір даних зазвичай представляє собою вибірку.

Зауважте, що STDEV і STDEV.S повертають однакові значення, тому ми можемо використовувати будь-яку функцію для обчислення вибіркового стандартного відхилення заданого набору даних.