Як розрахувати коефіцієнт phi в r

Коефіцієнт Phi (іноді його називають середньоквадратичним коефіцієнтом випадковості ) є мірою зв’язку між двома бінарними змінними.

Для таблиці 2×2, заданої для двох випадкових змінних x і y :

Коефіцієнт Phi можна розрахувати таким чином:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Приклад: обчислення коефіцієнта Phi у R

Припустімо, ми хочемо знати, чи пов’язана стать із перевагами політичної партії. Тож ми беремо просту випадкову вибірку з 25 виборців і запитуємо їх про їхні переваги щодо політичної партії.

У наступній таблиці представлені результати опитування:

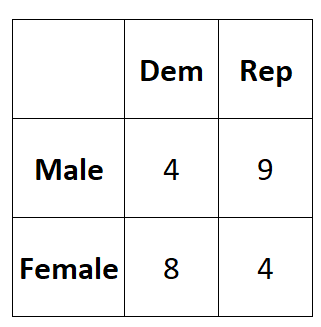
Ми можемо використати такий код, щоб ввести ці дані в матрицю 2×2 у R:

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

Потім ми можемо використати функцію phi() із пакета psych , щоб обчислити коефіцієнт Phi між двома змінними:

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Коефіцієнт Phi виявляється -0,36 .

Зауважте, що функція phi округлює до 2 цифр за замовчуванням, але ви можете вказати функцію округлення до будь-якої кількості цифр:

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

Як інтерпретувати коефіцієнт Phi

Подібно до коефіцієнта кореляції Пірсона, коефіцієнт Phi приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну залежність між двома змінними.
• 0 означає відсутність зв’язку між двома змінними.
• 1 вказує на абсолютно позитивний зв’язок між двома змінними.

Загалом, чим далі коефіцієнт Phi від нуля, тим сильніший зв’язок між двома змінними.

Іншими словами, чим далі коефіцієнт Phi від нуля, тим більше є доказів певного типу систематичної закономірності між двома змінними.

Додаткові ресурси

Знайомство з коефіцієнтом Фі
Калькулятор фі коефіцієнта