Абсолютне середнє відхилення проти стандартного відхилення: у чому різниця?
Стандартне відхилення є одним із найпоширеніших способів вимірювання поширення набору даних.
Він розраховується таким чином:
Стандартне відхилення = √( Σ(x i – x ) 2 / n )
Іншим способом вимірювання розподілу спостережень у наборі даних є середнє абсолютне відхилення .
Він розраховується таким чином:
Середнє абсолютне відхилення = Σ|x i – x | / ні
Цей підручник пояснює відмінності між цими двома показниками разом із прикладами того, як обчислити кожен.
Подібності та відмінності
Як випливає з їх назви, стандартне відхилення та середнє абсолютне відхилення намагаються кількісно визначити типове відхилення спостережень від середнього в даному наборі даних.
Однак метод , який використовується для кожного показника, відрізняється.
Стандартне відхилення
Стандартне відхилення визначає квадрат різниці між кожним спостереженням і середнім значенням набору даних. Потім він усереднює ці квадрати різниць і бере квадратний корінь.
Це залишає нам число, яке представляє «стандартне» або типове відхилення спостереження від середнього.
Означає абсолютне відхилення
І навпаки, середнє абсолютне відхилення визначає абсолютне відхилення між кожним спостереженням і середнім значенням набору даних. Потім він знаходить середнє значення цих відхилень.
Це залишає нам число, яке представляє середнє відхилення спостережень від середнього.
Оскільки стандартне відхилення визначає квадратичні різниці, воно завжди дорівнюватиме або перевищуватиме середнє абсолютне відхилення.
Якщо присутні екстремальні викиди, стандартне відхилення буде значно більшим, ніж середнє абсолютне відхилення. Наступний приклад ілюструє це.
Приклад: середнє абсолютне відхилення від стандартного відхилення
Припустимо, ми маємо такий набір даних із 8 значень:
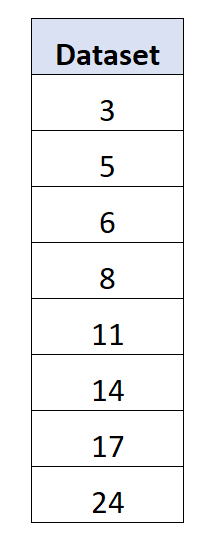
Середній показник виявляється 11 .
Отже, ми розрахуємо середнє абсолютне відхилення наступним чином:
Середнє абсолютне відхилення = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .
І ми б обчислили стандартне відхилення наступним чином:
Стандартне відхилення = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6,595 .
Як згадувалося раніше, стандартне відхилення завжди дорівнює або перевищує середнє абсолютне відхилення.
Однак різниця між стандартним відхиленням і середнім абсолютним відхиленням буде особливо великою, якщо в наборі даних є крайні викиди.
Наприклад, розглянемо наступний набір даних із крайнім викидом для останнього значення:
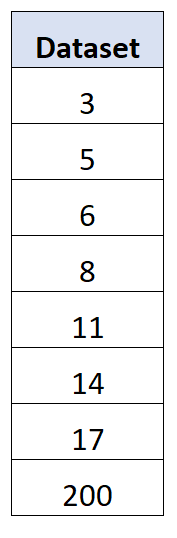
Виявляється, стандартне відхилення для цього набору даних становить 63,27 , тоді як середнє абсолютне відхилення становить 41,75 .
Екстремальний викид призводить до того, що стандартне відхилення набагато більше, ніж середнє абсолютне відхилення.
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше