Що таке спільний розподіл ймовірностей?
Двостороння частотна таблиця — це таблиця, яка відображає частоти (або «підрахунки») для двох категоріальних змінних.
Наприклад, наступна двостороння таблиця показує результати опитування 100 людей, який вид спорту вони віддають перевагу: бейсбол, баскетбол чи футбол.
У рядках відображається стать респондента, а в стовпцях вказується вид спорту, який вони обирають:

У цьому прикладі є дві змінні: спорт і стать.
Спільний розподіл ймовірностей просто описує ймовірність того, що дана особа приймає два певних значення для змінних.
Слово “кон’юнкт” походить від того, що нас цікавить ймовірність того, що дві речі відбуваються одночасно.
Наприклад, із загалом 100 осіб 13 були чоловіками та обрали своїм улюбленим видом спорту бейсбол.
Отже, ми б сказали, що загальна ймовірність того, що дана особа є чоловіком і обирає бейсбол своїм улюбленим видом спорту, становить 13/100 = 0,13 або 13% .
Записано в математичній нотації:
P(Стать = Чоловіча, Спорт = Бейсбол) = 13/100 = 0,13 .
Ми можемо використати цей процес для обчислення повного спільного розподілу ймовірностей:
- P (Стать = Чоловіча, Спорт = Бейсбол) = 13/100 = 0,13
- P(Стать = Чоловіча, Спорт = Баскетбол) = 15/100 = 0,15
- P(Стать = Чоловіча, Спорт = Футбол) = 20/100 = 0,20
- P (Стать = Жінка, Спорт = Бейсбол) = 23/100 = 0,23
- P(Стать = Жінка, Спорт = Баскетбол) = 16/100 = 0,16
- P(Стать = Жінка, Спорт = Футбол) = 13/100 = 0,13
Зауважте, що сума ймовірностей дорівнює 1 , або 100 % .
Навіщо використовувати спільний розподіл ймовірностей?
Спільні розподіли ймовірностей корисні, оскільки ми часто збираємо дані для двох змінних (наприклад, спорту та статі) і хочемо відповісти на запитання, пов’язані з обома змінними.
Наприклад, ми можемо захотіти зрозуміти ймовірність того, що певна особа в популяції є чоловіком і віддає перевагу бейсболу як своєму улюбленому виду спорту.
Або нам може бути цікаво зрозуміти ймовірність того, що дана особа є жінкою і віддає перевагу футболу як своєму улюбленому виду спорту.
Спільний розподіл ймовірностей може допомогти нам відповісти на ці запитання.
Використовуйте наступні приклади як практику, щоб краще зрозуміти спільний розподіл ймовірностей.
Приклад 1
У наведеній нижче двосторонній таблиці представлено результати опитування 238 людей, якому фільму вони віддають перевагу:
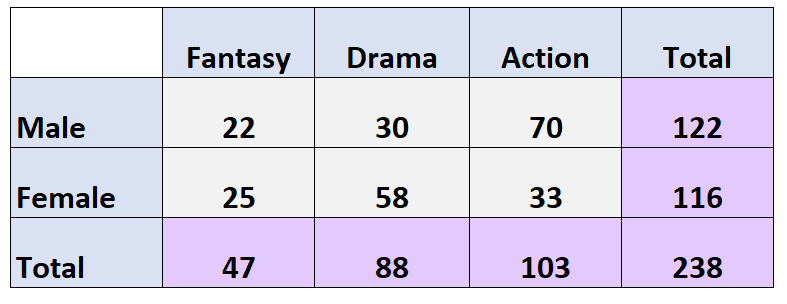
Запитання: Яка ймовірність того, що дана особа є жінкою і віддає перевагу драмі як своєму улюбленому кіножанру?
Відповідь: P (Стать = Жінка, Стать = Драма) = 58/238 = 0,244 = 24,4%
Приклад 2
У наведеній нижче двосторонній таблиці показано результати іспитів 64 студентів у класі залежно від кількості годин, які вони витратили на навчання:
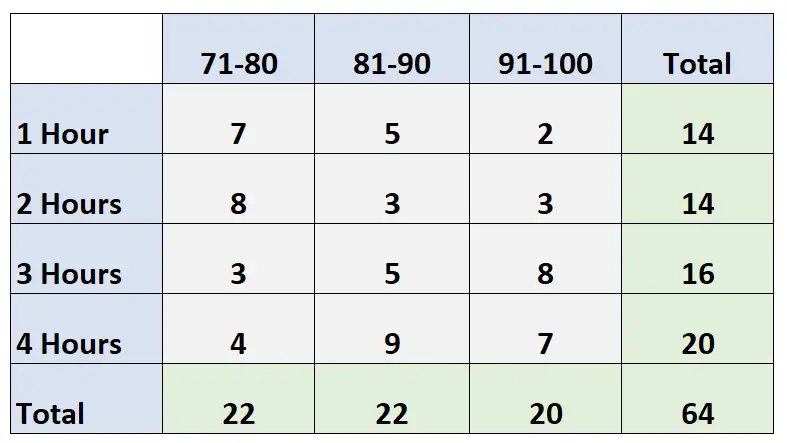
Запитання: Яка ймовірність того, що дана особа навчається 2 години і отримає оцінку від 91 до 100?
Відповідь: P (дослідження = 2 години, оцінка = 91-100) = 3/64 = 0,047 = 4,7%
Додаткові ресурси
Що таке граничний розподіл?
Як знайти умовну відносну частоту в таблиці подвійного запису