Як побудувати результати множинної лінійної регресії в r
Коли ми виконуємо просту лінійну регресію в R, легко візуалізувати підібрану лінію регресії, оскільки ми працюємо лише з однією змінною предиктором і однією змінною відповіді .
Наприклад, наведений нижче код показує, як підібрати просту модель лінійної регресії до набору даних і побудувати результати:
#create dataset data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11), y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41)) #fit simple linear regression model model <- lm(y ~ x, data = data) #create scatterplot of data plot(data$x, data$y) #add fitted regression line abline(model)
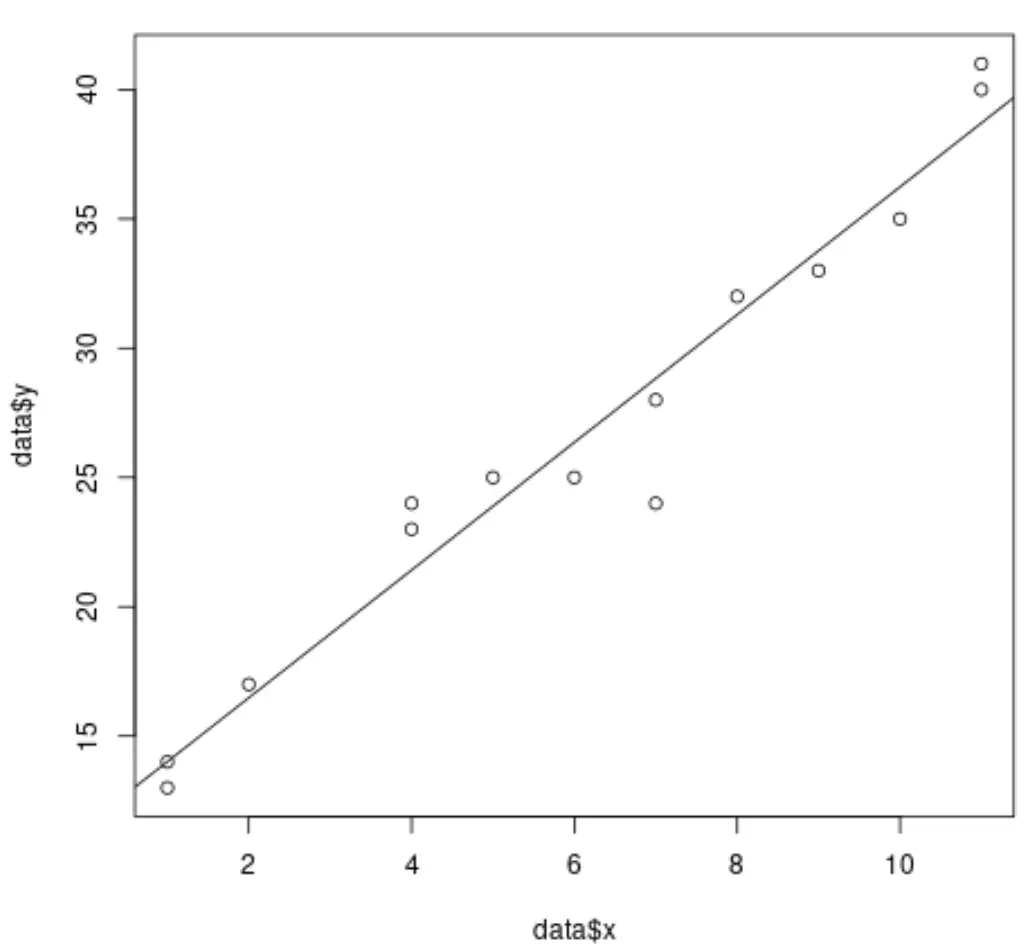
Однак, коли ми виконуємо множинну лінійну регресію, стає важко візуалізувати результати, оскільки існує кілька змінних прогностики, і ми не можемо просто побудувати лінію регресії на двовимірному графіку.
Замість цього ми можемо використовувати діаграми з доданими змінними (іноді їх називають «діаграми часткової регресії»), які являють собою окремі графіки, які відображають зв’язок між змінною відповіді та змінною предиктором, одночасно контролюючи присутність інших змінних предиктора в моделі .
У наступному прикладі показано, як виконати множинну лінійну регресію в R і візуалізувати результати за допомогою графіків доданих змінних.
Приклад: побудова графіка результатів множинної лінійної регресії в R
Припустімо, що ми адаптуємо наступну модель множинної лінійної регресії до набору даних у R за допомогою вбудованого набору даних mtcars :
#fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)
#view results of model
summary(model)
Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-5.1225 -1.8454 -0.4456 1.1342 6.4958
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 *
hp -0.031229 0.013345 -2.340 0.02663 *
drat 2.714975 1.487366 1.825 0.07863 .
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09
З результатів ми бачимо, що p-значення для кожного з коефіцієнтів менше 0,1. Для простоти ми припустимо, що кожна зі змінних предикторів є значущою і повинна бути включена в модель.
Щоб створити графіки доданих змінних, ми можемо використати функцію avPlots() із пакета автомобіля :
#load car package
library(car)
#produce added variable plots
avPlots(model)
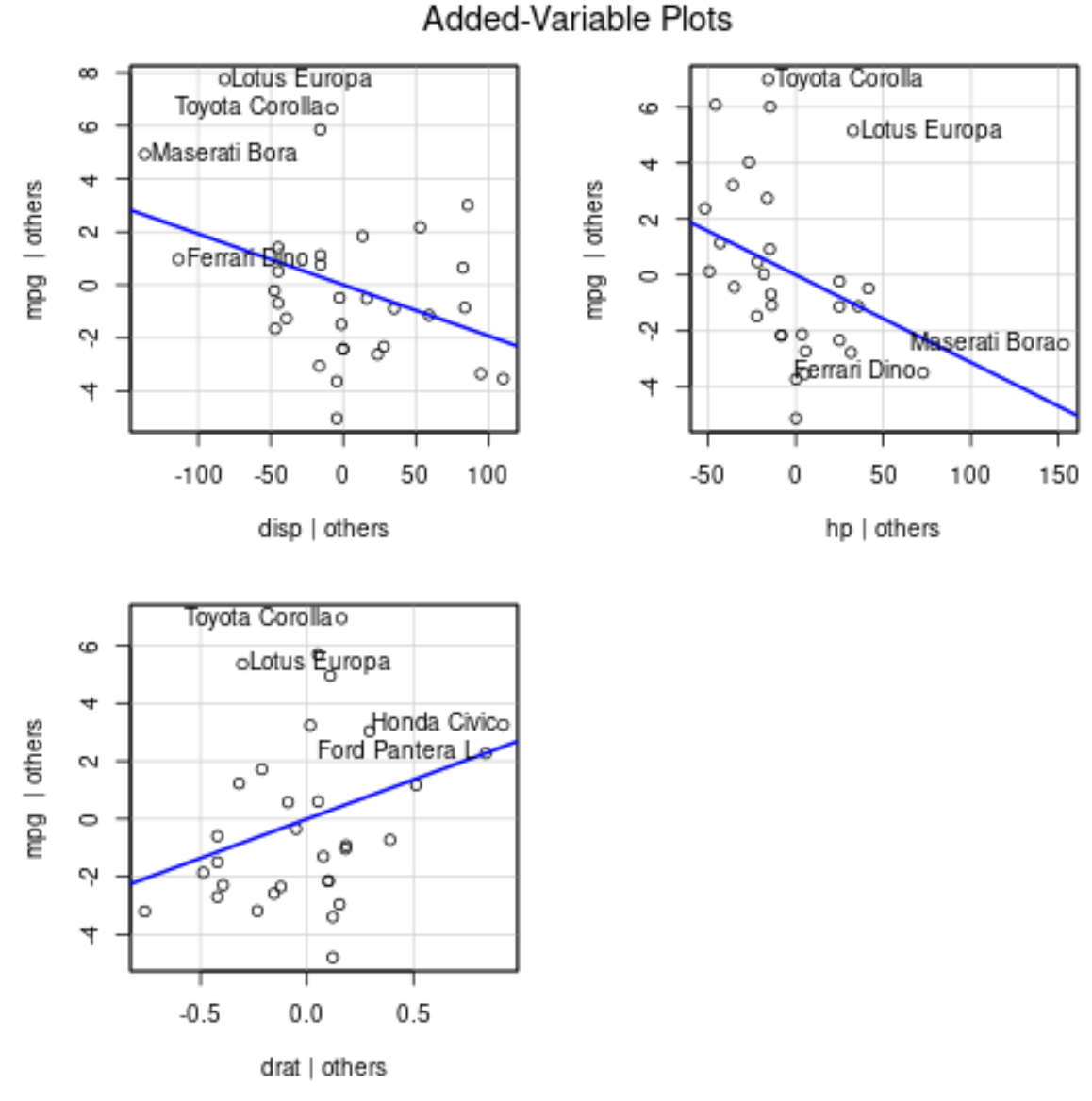
Ось як тлумачити кожен сюжет:
- На осі х відображається одна змінна предиктора, а на осі у – змінна відповіді.
- Блакитна лінія показує зв’язок між змінною предиктора та змінною відповіді, у той час як значення всіх інших змінних предиктора залишається постійним .
- Позначені точки на кожному графіку представляють 2 спостереження з найбільшими залишками та 2 спостереження з найбільшим частковим левериджем.
Зверніть увагу, що кут лінії на кожній діаграмі відповідає знаку коефіцієнта оцінюваного рівняння регресії.
Наприклад, ось оцінені коефіцієнти для кожної змінної предиктора в моделі:
- дисплей: -0,019232
- ch: -0,031229
- дата: 2.714975
Зауважте, що кут лінії додатний на графіку доданої змінної для drat , тоді як він є від’ємним для disp і hp , що відповідає знакам їхніх оцінених коефіцієнтів:
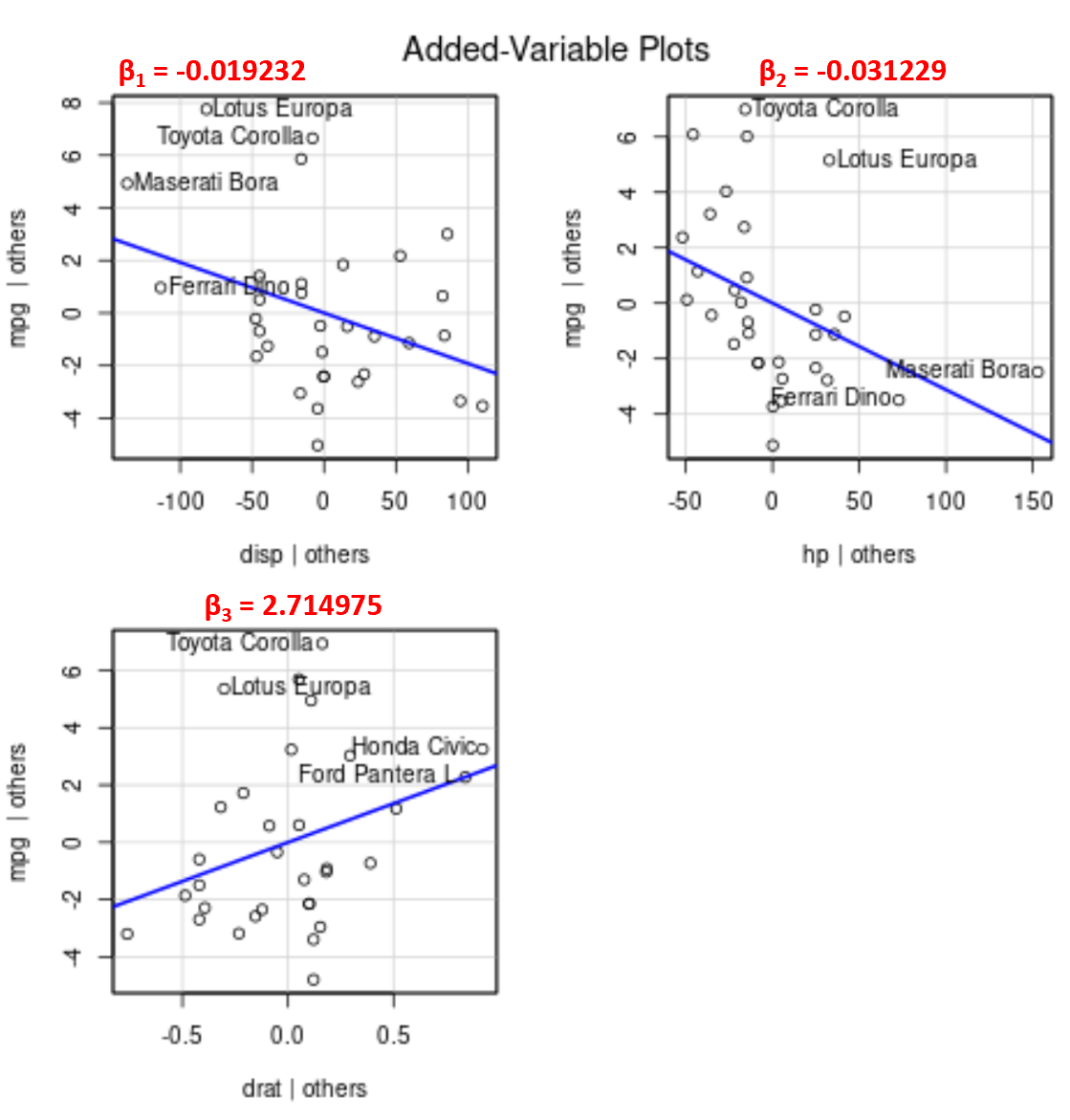
Хоча ми не можемо побудувати єдину підігнану лінію регресії на 2D-графіку, оскільки у нас є кілька змінних предиктора, ці додані графіки змінних дозволяють спостерігати зв’язок між кожною окремою змінною предиктора та змінною відповіді, утримуючи незмінними інші прогнозні змінні.