Як виконати квантильну регресію в python

Лінійна регресія – це метод, який ми можемо використати для розуміння зв’язку між однією або декількома змінними предиктора та змінною відповіді .

Як правило, коли ми виконуємо лінійну регресію, ми хочемо оцінити середнє значення змінної відповіді.

Однак замість цього ми могли б використати метод, відомий як квантильна регресія , щоб оцінити будь-яке значення квантиля або процентиля значення відповіді, наприклад 70-й процентиль, 90-й процентиль, 98-й процентиль тощо.

Цей підручник містить покроковий приклад того, як використовувати цю функцію для виконання квантильної регресії в Python.

Крок 1: Завантажте необхідні пакети

Спочатку ми завантажимо необхідні пакети та функції:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Крок 2: Створіть дані

Для цього прикладу ми створимо набір даних, який міститиме кількість вивчених годин і результати іспитів, отримані для 100 студентів університету:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Крок 3: Виконайте квантильну регресію

Далі ми підіб’ємо модель квантильної регресії, використовуючи вивчені години як змінну прогностику та оцінки за іспит як змінну відповіді.

Ми використаємо цю модель, щоб передбачити очікуваний 90-й процентиль іспитових балів на основі кількості вивчених годин:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

З результату ми можемо побачити оцінене рівняння регресії:

90-й процентиль оцінки за іспит = 59,6104 + 2,8495*(години)

Наприклад, 90-й процентиль усіх студентів, які навчаються 8 годин, має становити 82,4:

90-й процентиль іспитового балу = 59,6104 + 2,8495*(8) = 82,4 .

Вихідні дані також відображають верхню та нижню межі достовірності для перехоплення та часів змінної предиктора.

Крок 4: Візуалізуйте результати

Ми також можемо візуалізувати результати регресії, створивши діаграму розсіювання з підігнаним квантильним рівнянням регресії, накладеним на графік:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

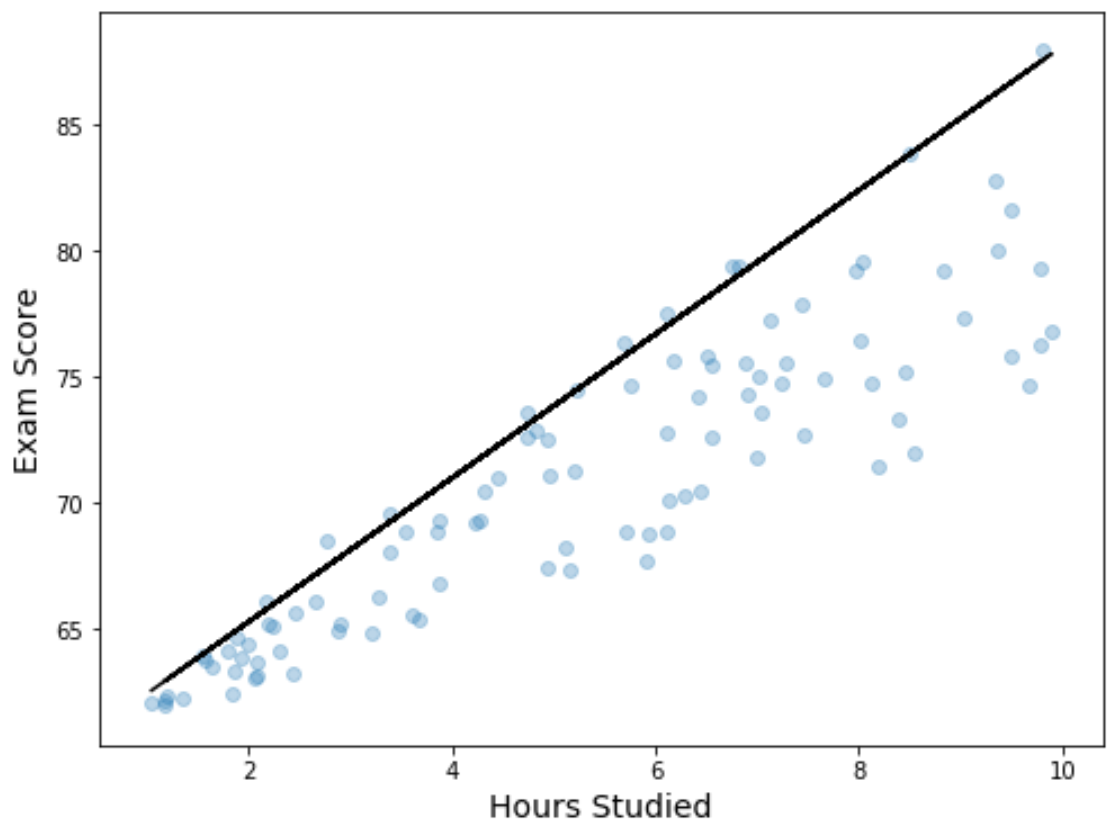
На відміну від простої лінії лінійної регресії, зауважте, що ця підібрана лінія не є «лінією найкращого підходу» для даних. Натомість він проходить через розрахунковий 90-й процентиль на кожному рівні змінної предиктора.

Додаткові ресурси

Як виконати просту лінійну регресію в Python
Як виконати квадратичну регресію в Python