Що таке дихотомічні змінні? (визначення & #038; приклад)

Дихотомічна змінна — це тип змінної, яка приймає лише два можливі значення.

Ось кілька прикладів дихотомічних змінних:

• Стать: чоловіча або жіноча
• Підкидання монети: орла або решка
• Тип нерухомості: Житлова або Комерційна
• Статус спортсмена: Професіонал або Любитель
• Результати іспиту: склав або не склав

Ці типи змінних постійно виникають на практиці. Наприклад, розглянемо наступний набір даних, який містить 10 спостережень і 4 змінні:

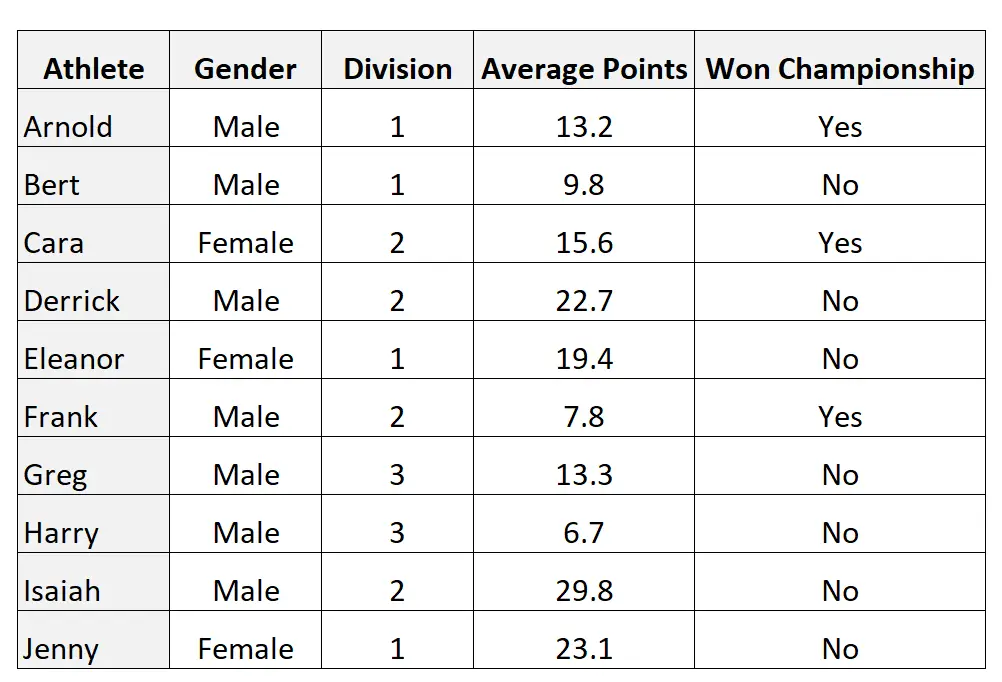
Змінні стать і виграний чемпіонат є дихотомічними, оскільки кожна з них може приймати лише два можливі значення:

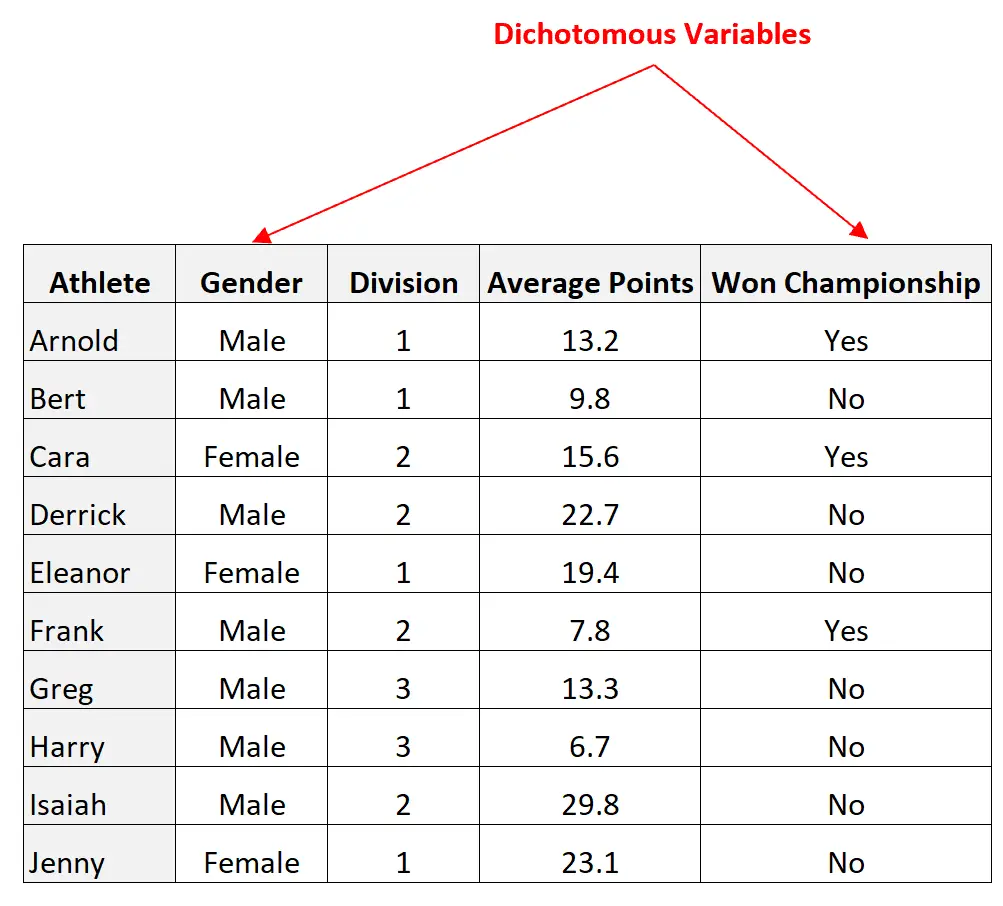
Однак змінні Division і Average Points не є дихотомічними, оскільки вони можуть приймати кілька значень.

Бонусна порада:

Ви можете пам’ятати, що дихотомічні змінні можуть приймати лише два значення, пам’ятаючи, що префікс «di» є грецьким словом, що означає «два», «двічі» або «подвійний».

Як створити дихотомічні змінні

Слід зазначити, що ми можемо створити дихотомічну змінну з безперервної змінної, просто відокремивши значення на основі певного порогу.

Наприклад, у попередньому наборі даних ми могли перетворити змінну Average Points на дихотомічну змінну, класифікувавши гравців із середнім показником вище 15 як «хороших бомбардирів», а тих із середнім показником нижче 15 як «поганих бомбардирів»:

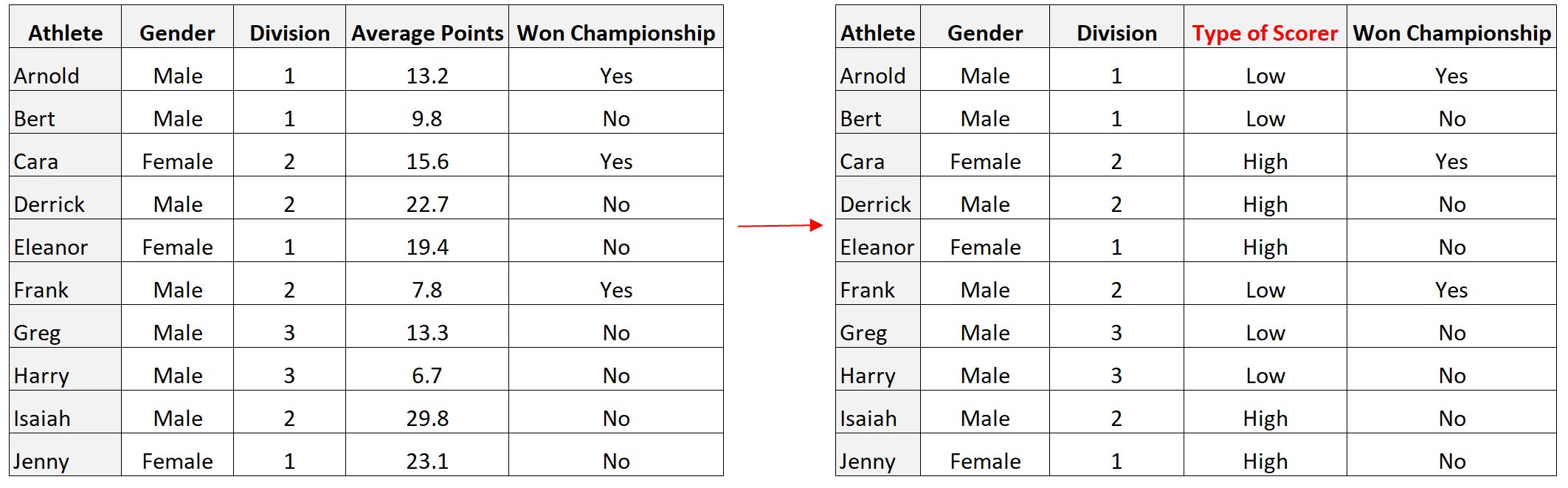
Як візуалізувати дихотомічні змінні

Зазвичай ми візуалізуємо дихотомічні змінні за допомогою простої гістограми, щоб представити частоти кожного значення, яке вони можуть прийняти.

Наприклад, наступна гістограма показує частоти кожної статі в попередньому наборі даних:

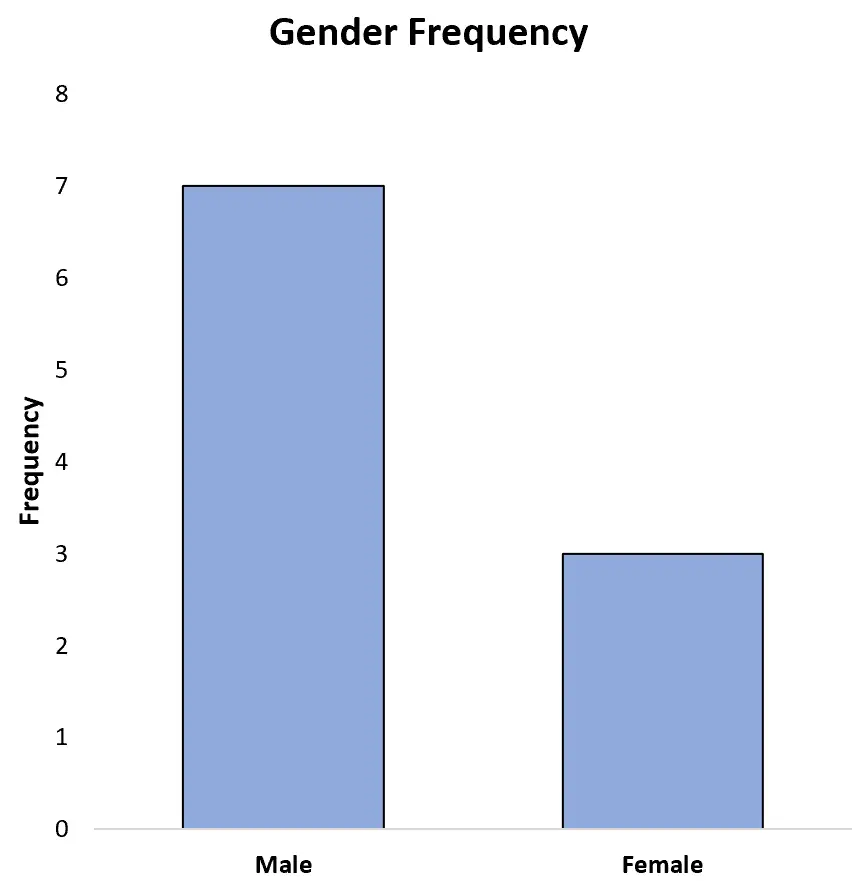
Ми також можемо відобразити частоти у відсотках на осі y:

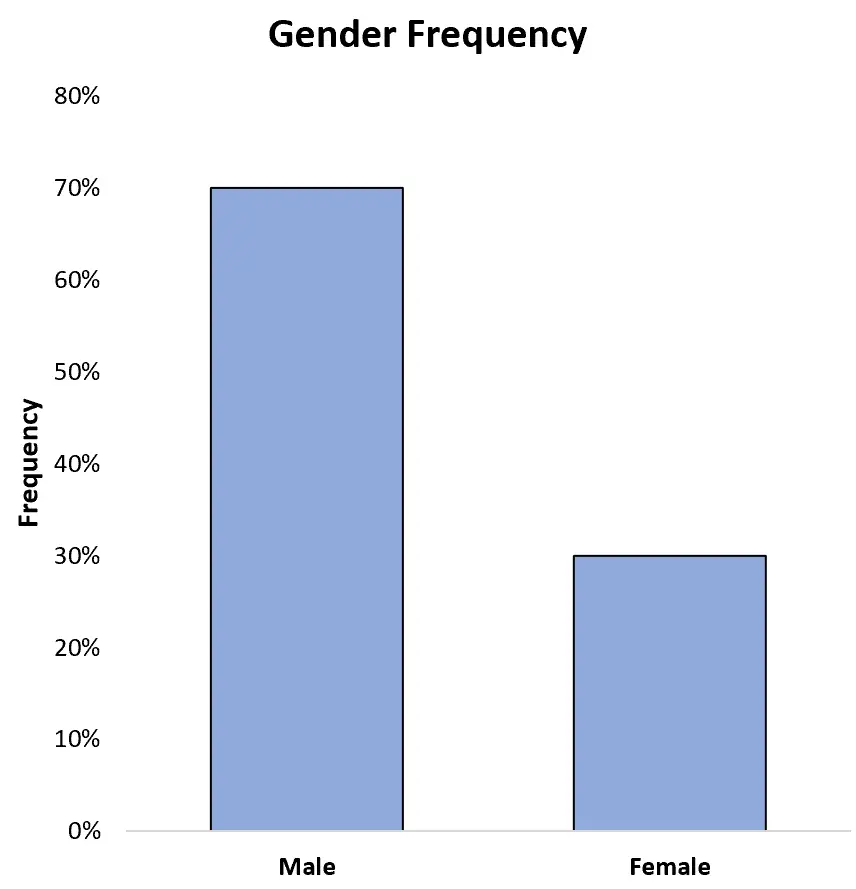
Це дозволяє нам легко побачити, що 70% від загальної кількості спортсменів у наборі даних – чоловіки, а 30% – жінки.

Як аналізувати дихотомічні змінні

Існує кілька способів аналізу дихотомічних змінних. Два найпоширеніші методи включають:

1. Однопропорційний z-тест

Однопропорційний z-тест визначає, чи дорівнює спостережувана пропорція теоретичній пропорції.

Наприклад, ми могли б використати цей тест, щоб визначити, чи дорівнює справжня частка чоловіків-спортсменів у певній сукупності 50%.

2. Точково-бісеріальна кореляція

Точково-бісерійна кореляція використовується для вимірювання зв’язку між дихотомічною змінною та безперервною змінною.

Цей тип кореляції приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну кореляцію між двома змінними
• 0 означає відсутність кореляції між двома змінними
• 1 вказує на абсолютно позитивну кореляцію між двома змінними

Наприклад, ми могли б обчислити бісерійну кореляцію між статтю та середніми очками за гру, щоб зрозуміти, наскільки тісно пов’язані ці дві змінні.