Тест брейша-пейгана: визначення та приклад
Одне з ключових припущень лінійної регресії полягає в тому, що залишки розподіляються з рівною дисперсією на кожному рівні змінної предиктора. Це припущення відоме як гомоскедастичність .
Якщо це припущення не виконується, кажуть, що гетероскедастичність присутня в залишках. Коли це відбувається, результати регресії стають ненадійними.
Один із способів візуально визначити наявність гетероскедастичності — це створити графік залишків проти підігнаних значень із моделі регресії.
Якщо залишки розповсюджуються більше при більш високих значеннях на графіку, це свідчить про наявність гетероскедастичності.
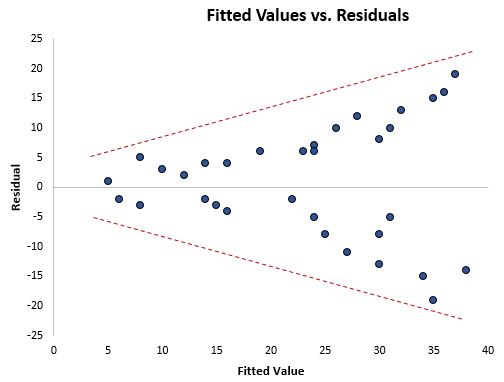
Формальним статистичним тестом, який ми можемо використовувати для визначення наявності гетероскедастичності, є тест Брейша-Пейгана .
Цей підручник містить коротке пояснення тесту Брейша-Пейгана разом із прикладом.
Що таке тест Брейша-Пагана?
Критерій Брейша-Пейгана використовується для визначення наявності гетероскедастичності в регресійній моделі.
Тест використовує такі нульові та альтернативні гіпотези :
- Нульова гіпотеза (H 0 ): наявна гомоскедастичність (залишки розподіляються з рівною дисперсією)
- Альтернативна гіпотеза ( HA ): наявна гетероскедастичність (залишки не розподілені з рівною дисперсією)
Якщо p-значення тесту нижче певного рівня значущості (тобто α = 0,05), тоді ми відхиляємо нульову гіпотезу та робимо висновок, що гетероскедастичність присутня в регресійній моделі.
Ми використовуємо наступні кроки для виконання тесту Брейша-Пейгана:
1. Підібрати регресійну модель.
2. Обчислити квадрати модельних нев’язок.
3. Підберіть нову модель регресії, використовуючи квадрати залишків як значення відповіді.
4. Обчисліть тестову статистику хі-квадрат X 2 у формі n*R 2 new , де:
- n: Загальна кількість спостережень
- R 2 new : R у квадраті нової регресійної моделі, яка використовувала квадрати залишків як значення відповіді
Якщо значення p, яке відповідає цій статистиці тесту хі-квадрат із p (кількістю предикторів) ступенів свободи, нижче певного рівня значущості (тобто α = 0,05), тоді відхиліть нульову гіпотезу та зробіть висновок про наявність гетероскедастичності. .
В іншому випадку не відкидайте нульову гіпотезу. У цьому випадку передбачається наявність гомоскедастичності.
Зауважте, що більшість статистичних програм може легко виконати тест Брейша-Пейгана, тож вам, ймовірно, ніколи не доведеться виконувати ці дії вручну, але корисно знати, що відбувається за лаштунками.
Приклад тесту Брейша-Пагана
Припустимо, що ми маємо наступний набір даних, що містить інформацію про 10 різних баскетболістів:
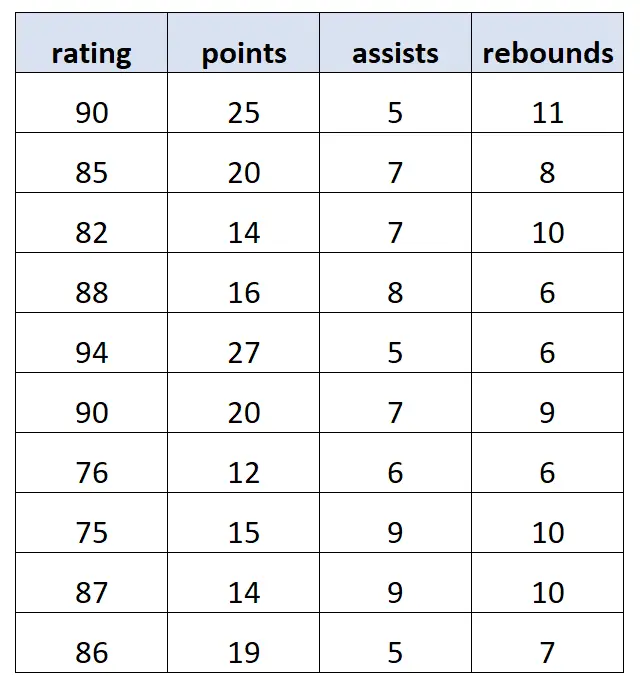
Використовуючи статистичне програмне забезпечення, ми підібрали наступну модель множинної лінійної регресії :
рахунок = 62,47 + 1,12*(очки) + 0,88*(ассисти) – 0,43*(підбирання)
Потім ми використовуємо цю модель, щоб зробити прогнози щодо рейтингу кожного гравця та обчислити квадрати залишків (тобто квадрат різниці між прогнозованим рейтингом і фактичним рейтингом):
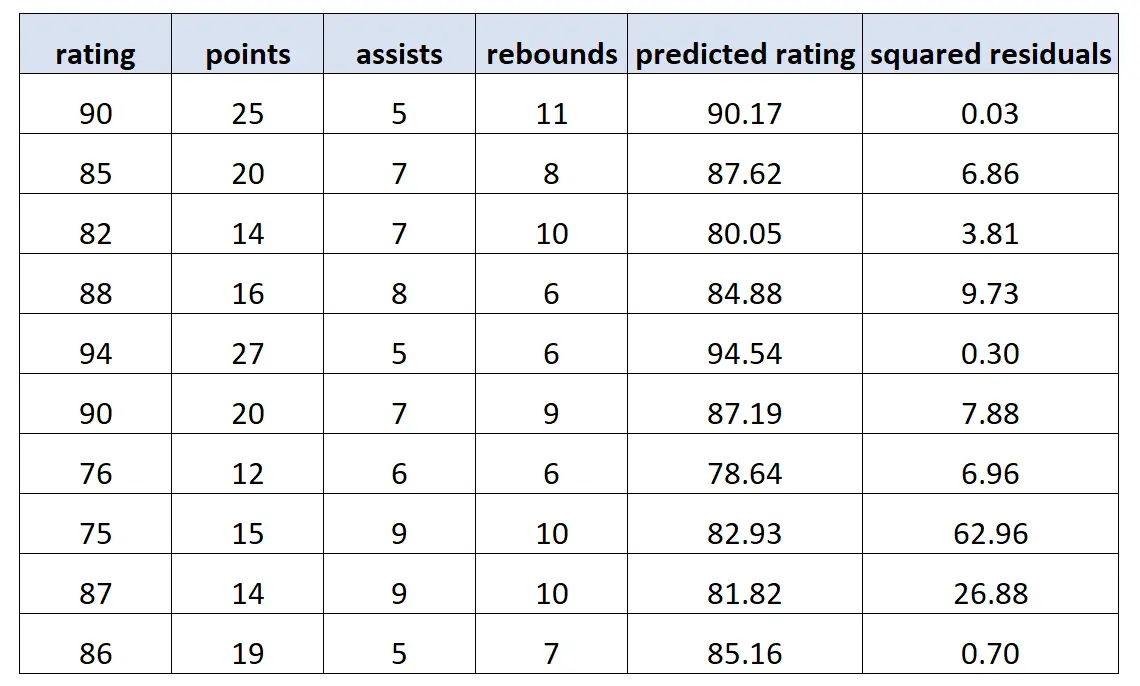
Далі ми підбираємо нову регресійну модель, використовуючи квадрати залишків як значення відповіді та вихідні змінні предиктора як змінні предиктора. Ми знайшли наступне:
- n: 10
- R 2 новий : 0,600395
Отже, наша статистика хі-квадрат для тесту Брейша-Пейгана становить n*R 2 new = 10*.600395 = 6.00395 . Ступені свободи є p = 3 змінними предикторів.
Відповідно до калькулятора хі-квадрат до значення P , значення p, яке відповідає X 2 = 6,00395 із 3 ступенями свободи, дорівнює 0,111418 .
Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. Тому ми припускаємо, що гомоскедастичність присутня.
Проба Брейша-Пагана на практиці
Наступні навчальні посібники надають покрокові приклади виконання тесту Брейша-Пейгана в різних статистичних програмах:
Як виконати тест Брейша-Пагана в Excel
Як виконати тест Брейша-Пейгана в R
Як виконати тест Брейша-Пагана в Python
Як виконати тест Брейша-Пагана в Stata