Що таке я моран? (визначення & #038; приклад)

І Морана — це спосіб вимірювання просторової автокореляції.

Простіше кажучи, це спосіб кількісно визначити, наскільки тісно кластеризовані значення у 2D-просторі. Він часто використовується в географії та географічній інформаційній науці (ГІС) для вимірювання того, наскільки тісно згруповані різні об’єкти на карті, наприклад дохід сім’ї, рівень освіти тощо.

Моран І: формула

Формула для розрахунку І Морана така:

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

золото:

• N: кількість просторових одиниць з індексами i та j
• W: сума всіх w _ij
• x: змінна інтересу (дохід домогосподарства, роки навчання тощо)
• x : середнє значення x
• w _ij : матриця просторових ваг

Ймовірно, вам ніколи не доведеться обчислювати цей показник вручну, оскільки більшість статистичних програм може обчислити його за вас, але це допоможе знати формулу, яка використовується під капотом.

Значення I Морана може коливатися від -1 до 1, де:

• -1: змінна, що цікавить, ідеально розсіяна
• 0: змінна, що цікавить, розсіяна випадковим чином
• 1: Змінна, що цікавить, ідеально згрупована

Разом із обчисленням І Морана більшість статистичних програм обчислює відповідне значення p, яке можна використовувати для визначення того, випадково розсіяні дані чи ні.

Тест Морана використовує такі нульові та альтернативні гіпотези:

Нульова гіпотеза (H ₀ ): дані розкидані випадковим чином.

Альтернативна гіпотеза ( _HA ): Дані не розпорошені випадковим чином, тобто вони згруповані за видимими моделями.

Якщо p-значення, яке відповідає I Морана, нижче певного рівня значущості (тобто α = 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що дані просторово згруповані таким чином, що вони навряд чи будуть просторово згруповані. сталася випадково.

Moran’s I: кілька прикладів

Наступні приклади представляють фальшиві карти з різними значеннями для І Морана.

Припустімо, що кожен квадрат на карті позначає округ, а округи із середнім доходом сім’ї понад 50 000 доларів США позначені синім кольором.

І Морана = 0: середній дохід домогосподарства випадково розподілений (тобто випадкові кластери у випадкових областях).

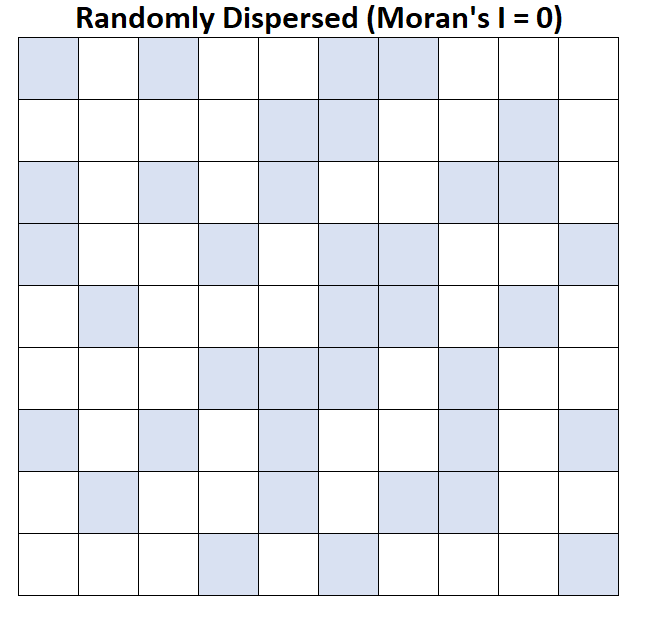
І Морана = -1: середній дохід домогосподарства ідеально розподілений.

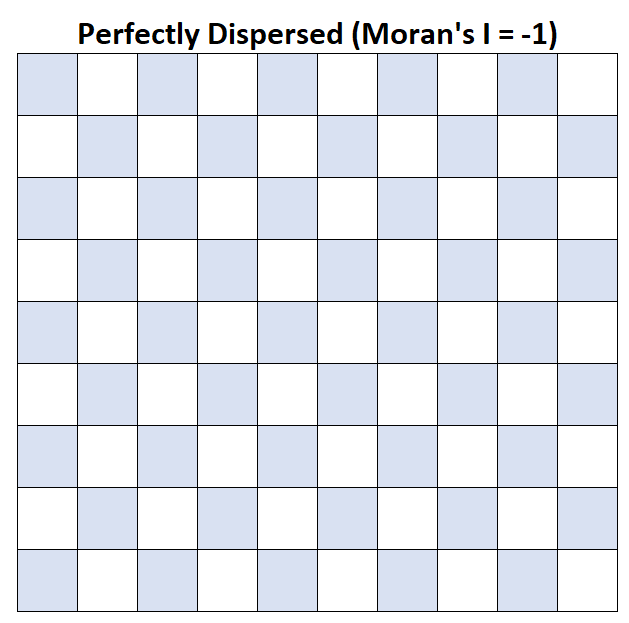
I Морана = 1: середній дохід домогосподарства ідеально згрупований.

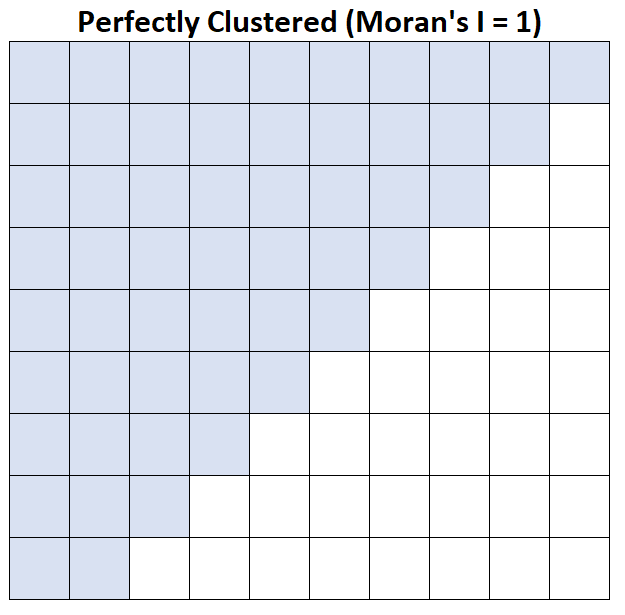
Зверніться до цього прикладу для конкретного прикладу обчислення І Морана в статистичному програмному забезпеченні R.