Верхня та нижня огорожі: визначення та приклад
У статистиці верхня та нижня межі представляють порогові значення для верхнього та нижнього викидів у наборі даних. Вони розраховуються таким чином:
- Нижнє закриття = Q1 – (1,5*IQR)
- Верхнє закриття = Q3 + (1,5*IQR)
де IQR означає «міжквартильний діапазон», який представляє різницю між 75-м процентилем (Q3) і 25-м процентилем (Q1) у наборі даних.
Спостереження , розташоване вище верхнього або нижче нижнього бар’єру, часто вважається викидом.

Приклад: Розрахунок верхньої та нижньої огорожі
Припустимо, що ми маємо наступний набір даних:
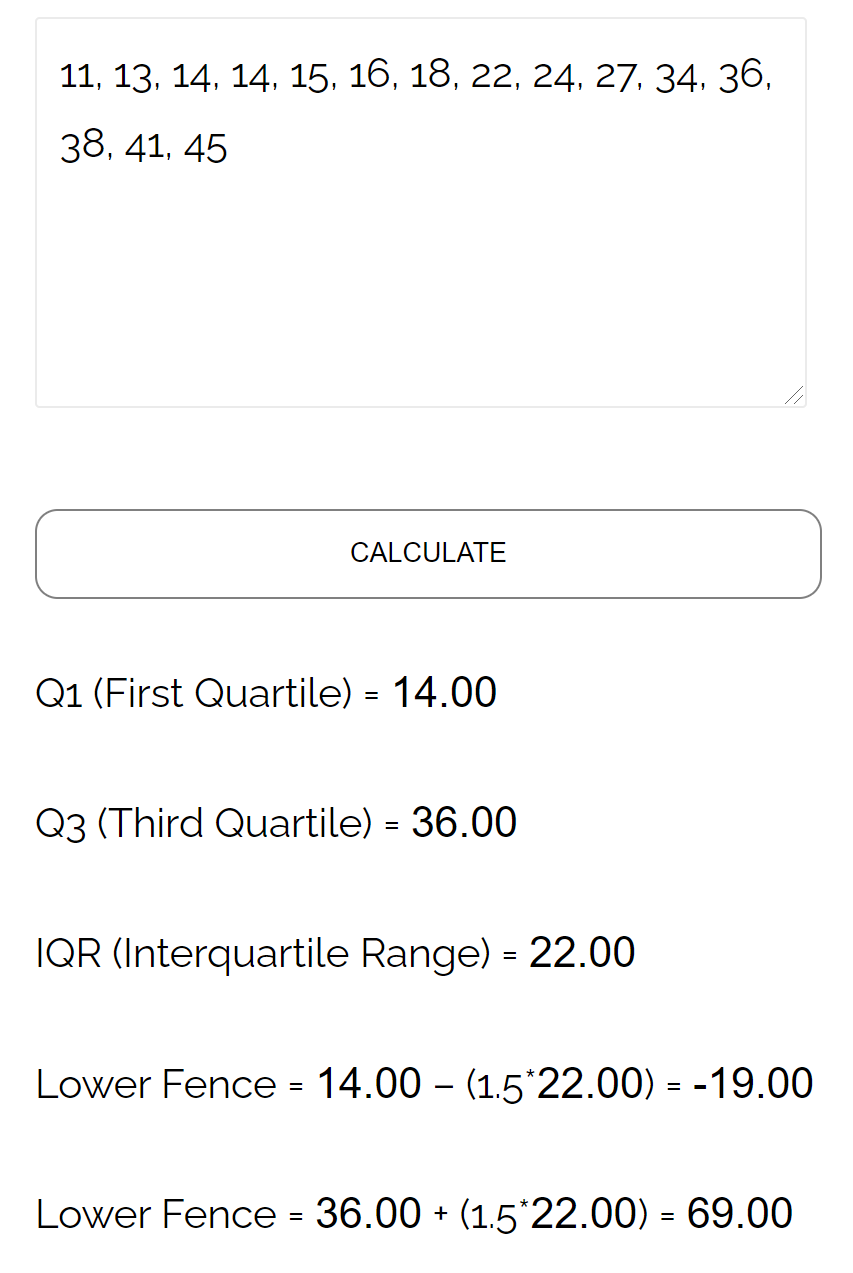
Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45
Ми можемо використати такі кроки, щоб обчислити верхню та нижню межу набору даних:
Крок 1. Знайдіть Q1 і Q3.
Q1 представляє 25-й процентиль набору даних, а Q3 — 75-й процентиль. Відповідно до калькулятора інтерквартильного діапазону Q1 і Q3 для цього набору даних є:
- Т1: 14
- Т3: 36
Крок 2: Знайдіть IQR (міжквартильний діапазон).
Міжквартильний діапазон представляє різницю між Q3 і Q1, яка розраховується таким чином:
- Міжквартильна шкала: Q3 – Q1 = 36 – 14 = 22
Крок 3: Знайдіть верхню та нижню огорожу
Для розрахунку верхньої та нижньої огорож можна використовувати такі формули:
- Нижнє закриття: Q1 – (1,5*IQR) = 14 – (1,5*22) = -19
- Верхня огорожа: Q3 + (1,5*IQR) = 36 + (1,5*22) = 69
Оскільки жодне зі спостережень у нашому наборі даних не опускається нижче нижнього або вище верхнього паркану, жодне зі спостережень не вважатиметься викидом.
Ми також можемо створити коробковий графік , щоб візуалізувати наш розподіл значень даних, а також верхню та нижню межі:

Бонус: калькулятор верхнього та нижнього закриття
Замість того, щоб вручну обчислювати верхню та нижню межі набору даних, сміливо скористайтеся калькулятором верхньої та нижньої меж:
Ви можете знайти більше корисних статистичних калькуляторів на цій сторінці .