Як знайти середнє значення розподілу ймовірностей: із прикладами

Розподіл ймовірностей говорить нам про ймовірність того, що випадкова величина набуває певних значень.

Наприклад, наступний розподіл ймовірностей говорить нам про ймовірність того, що певна футбольна команда заб’є певну кількість голів у даному матчі:

Примітка. Сума ймовірностей у дійсному розподілі ймовірностей завжди дорівнює 1. Ми можемо підтвердити, що цей розподіл ймовірностей є дійсним: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.

Щоб знайти середнє (іноді його називають «очікуваним значенням») розподілу ймовірностей, ми можемо використати таку формулу:

 Mean (Or "Expected Value") of a Probability Distribution:

μ = Σx * P(x)

where:
•x: Data value
    •P(x): Probability of value

Наприклад, розглянемо наш розподіл ймовірностей для футбольної команди:

Середня кількість голів футбольної команди розраховується наступним чином:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гол.

У наведених нижче прикладах показано, як обчислити середнє значення розподілу ймовірностей у кількох інших сценаріях.

Приклад 1: Середня кількість поломок автомобіля

Наступний розподіл ймовірностей говорить нам про ймовірність того, що даний автомобіль зазнає певної кількості відмов акумулятора протягом 10-річного періоду:

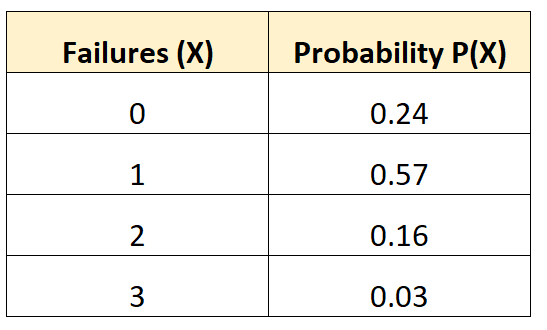
Питання: Яка середня кількість поломок очікується для цього автомобіля?

Рішення: середня кількість очікуваних відмов розраховується наступним чином:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 відмов.

Приклад 2: середня кількість виграшів

Наступний розподіл ймовірностей говорить нам про ймовірність того, що дана баскетбольна команда виграє певну кількість ігор у турнірі:

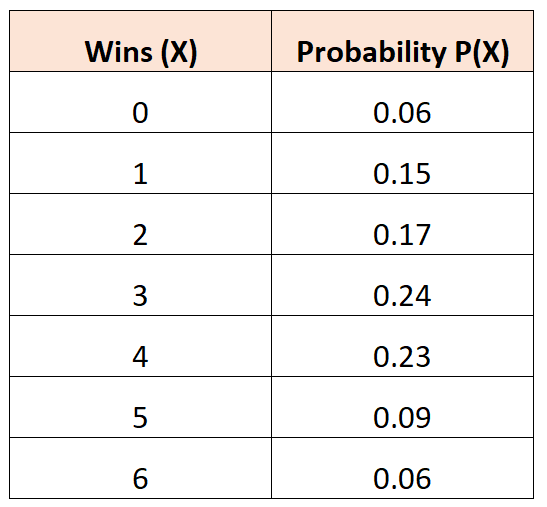
Запитання: Яка середня кількість перемог очікується для цієї команди?

Рішення: Середня кількість очікуваних виграшів розраховується наступним чином:

μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 виграшів.

Приклад 3: середня кількість продажів

Наступний розподіл ймовірностей говорить нам про ймовірність того, що даний продавець зробить певну кількість продажів у наступному місяці:

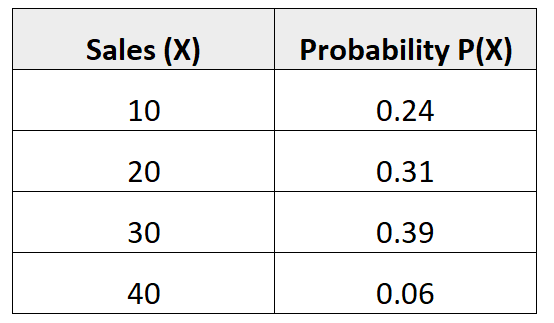
Питання: Яка середня кількість продажів очікується для цього продавця в наступному місяці?

Рішення: середня кількість очікуваних продажів розраховується наступним чином:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 брудних.

Бонус: калькулятор розподілу ймовірностей

Ви можете використовувати цей калькулятор для автоматичного обчислення середнього будь-якого розподілу ймовірностей.