Що таке непересічні події? (визначення та приклади)

Непересічні події — це події, які не можуть відбуватися одночасно.

Записані в імовірнісній нотації, події A і B є непересічними, якщо їх перетин дорівнює нулю. Це можна записати так:

• P(A і B) = 0
• P(A∩B) = 0

Наприклад, припустімо, що ми навмання вибираємо карту з колоди. Нехай подія A — це подія, коли карта є піковою або трефовою, а подія B — це подія, коли карта є червовою або бубновою.

Ми б визначили вибірковий простір для подій наступним чином:

• A = {піка, трефа}
• B = {Серце, Діамант}

Зверніть увагу, що між двома вибірковими просторами немає перекриття. Таким чином, події A і B є непересічними подіями, оскільки обидві вони не можуть відбутися одночасно.

Примітка. Непересічні події також називаються взаємовиключними .

Приклади непересічних подій

Ось ще кілька прикладів непересічних подій.

Приклад 1: нічия

Припустимо, ви підкинули монету. Нехай подія A — це подія, коли монета потрапляє на орди, а подія B — подія, коли монета потрапляє на орди.

Подія A і B були б непересічними, оскільки вони не можуть відбутися одночасно. Монета не може впасти на орла або решку.

Приклад 2: кидання кубиків

Припустимо, ви кидаєте кубик. Нехай подія A — це подія, коли кубик падає на непарне число, а подія B — подія, коли кубик падає на парне число.

Подія A і B були б непересічними, оскільки вони не можуть відбутися одночасно. Гральний кубик не може випасти на парне число і на непарне число.

Приклад 3: Розташування Pro Bowl

Припустімо, НФЛ хоче вибрати місце для проведення Pro Bowl. Вони звузили вибір у Маямі та Сан-Дієго. Вони кладуть два імені в капелюх і вибирають одне навмання. Припустімо, що Подія A – це подія, для якої вони вибрали Маямі, а Подія B – це подія, для якої вони вибрали Сан-Дієго.

Подія A і B були б непересічними, оскільки вони не можуть відбутися одночасно. Майамі та Сан-Дієго не можна вибрати.

Перегляд непересічних подій

Корисним способом візуалізації непересічних подій є створення діаграми Венна.

Якщо дві події не перетинаються , вони взагалі не перекриватимуться на діаграмі Венна:

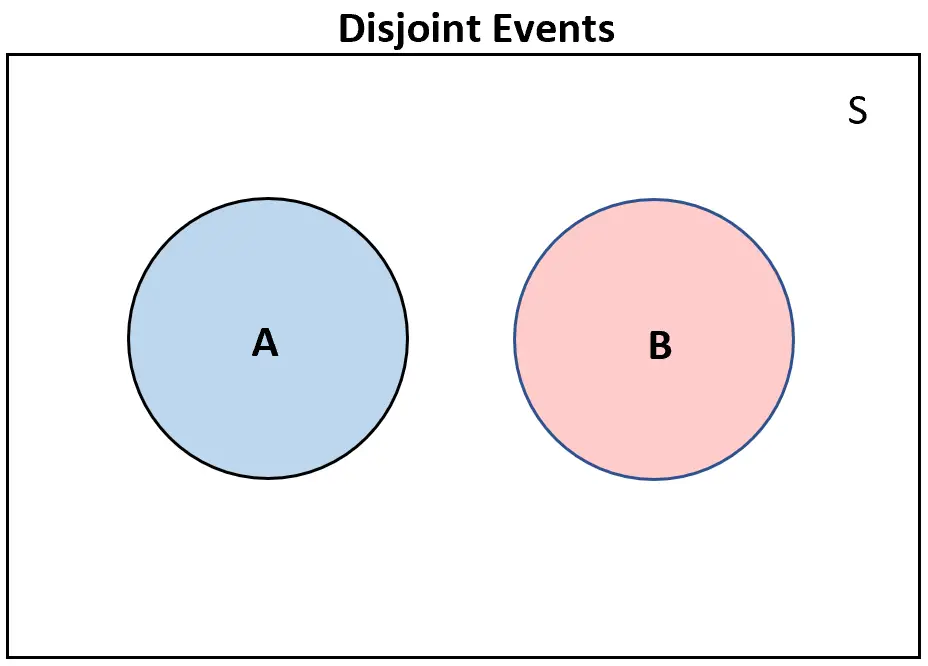
І навпаки, якщо дві події не перетинаються , діаграма Венна буде принаймні деяким перекриттям:

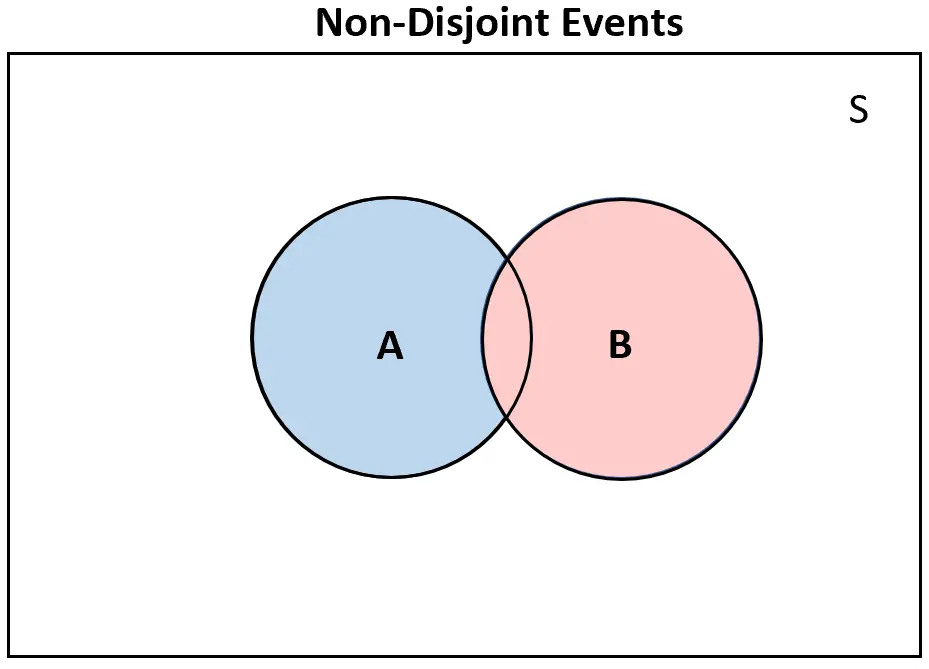
Імовірність непересічних подій

Як згадувалося раніше, якщо дві події не перетинаються, ймовірність того, що вони відбудуться одночасно, дорівнює нулю.

• P(A∩B) = 0

Подібним чином, ймовірність будь-якої події може бути розрахована шляхом додавання їхніх індивідуальних ймовірностей.

• P(A∪B) = P(A) + P(B)

Наприклад, нехай подія A — це подія, коли кубик падає на 1 або 2, а подія B — це подія, коли кубик падає на 5 або 6.

Ми б визначили вибірковий простір для подій наступним чином:

• A = {1, 2}
• B = {5, 6}

Ми обчислюємо ймовірність події A або події B як:

• P(A∪B) = P(A) + P(B)
• P(A∪B) = 2/6 + 2/6
• P(A∪B) = 4/6 = 2/3

Імовірність події A або B дорівнює 2/3 .

Додаткові ресурси

Наступні навчальні посібники містять пояснення інших поширених тем про ймовірність:

Як знайти ймовірність А або В: з прикладами
Як знайти ймовірність A і B: на прикладах
Закон повної ймовірності: визначення та приклади