Коефіцієнт асиметрії пірсона в excel (покроково)

Коефіцієнт асиметрії Пірсона , розроблений біостатистиком Карлом Пірсоном , є способом вимірювання асиметрії у вибірці даних.

Фактично існує два методи, які можна використовувати для розрахунку коефіцієнта асиметрії Пірсона:

Спосіб 1: Використовуйте режим

Асиметрія = (середнє – режим) / стандартне відхилення вибірки

Спосіб 2: Використання медіани

Асиметрія = 3 (середнє – медіана) / стандартне відхилення вибірки

Загалом, другий метод є кращим, оскільки режим не завжди є хорошим показником того, де лежить «центральне» значення набору даних, і в наборі даних може бути більше одного режиму.

У наступному покроковому прикладі показано, як обчислити обидві версії коефіцієнта асиметрії Пірсона для певного набору даних у Excel.

Крок 1: Створіть набір даних

Спочатку давайте створимо такий набір даних в Excel:

Крок 2. Обчисліть коефіцієнт асиметрії Пірсона (з використанням режиму)

Тоді ми можемо використати наступну формулу для розрахунку коефіцієнта асиметрії Пірсона за допомогою режиму:

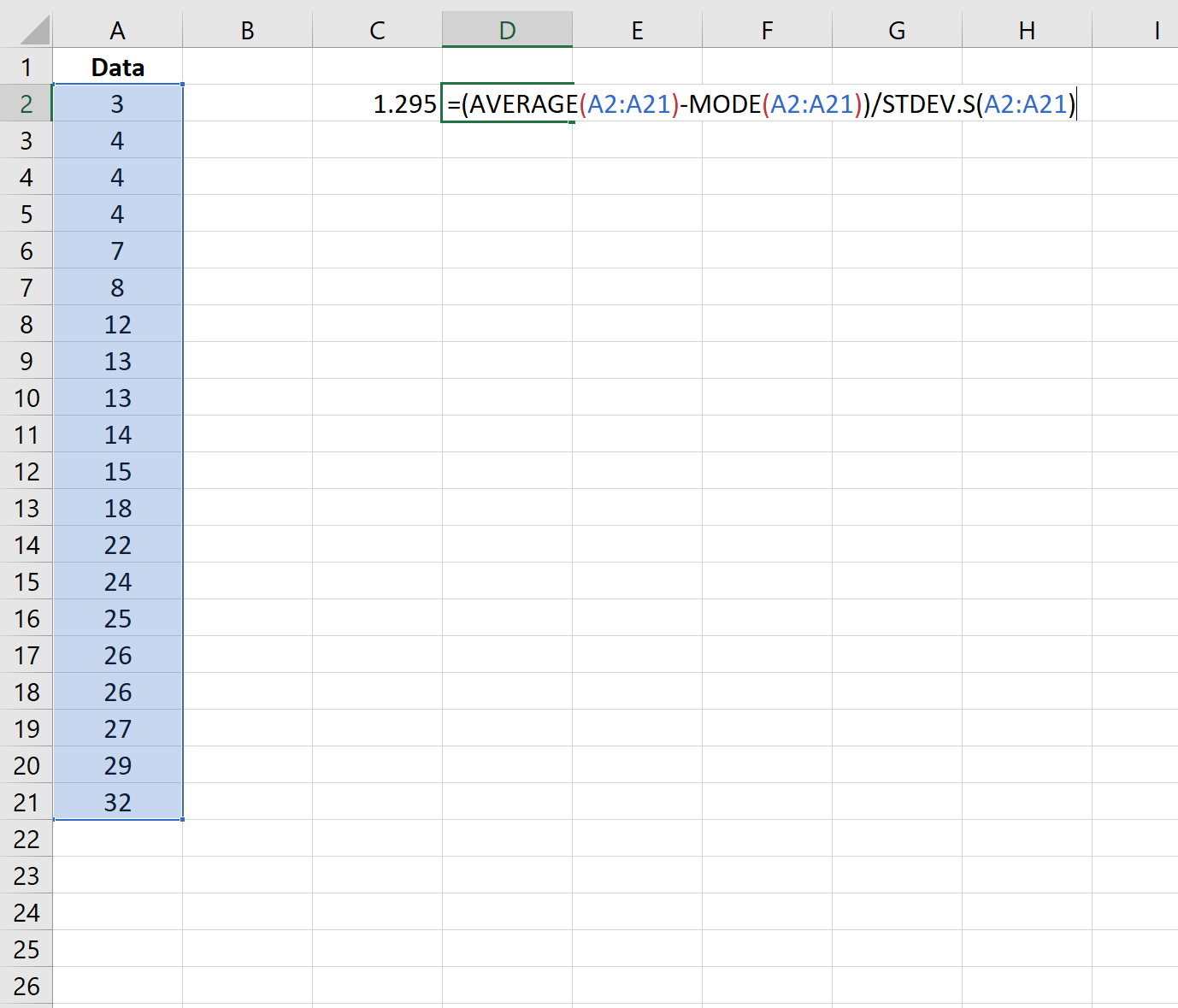
Асиметрія виявляється рівною 1,295 .

Крок 3. Обчисліть коефіцієнт асиметрії Пірсона (використовуючи медіану)

Ми також можемо використати наступну формулу для розрахунку коефіцієнта асиметрії Пірсона за допомогою медіани:

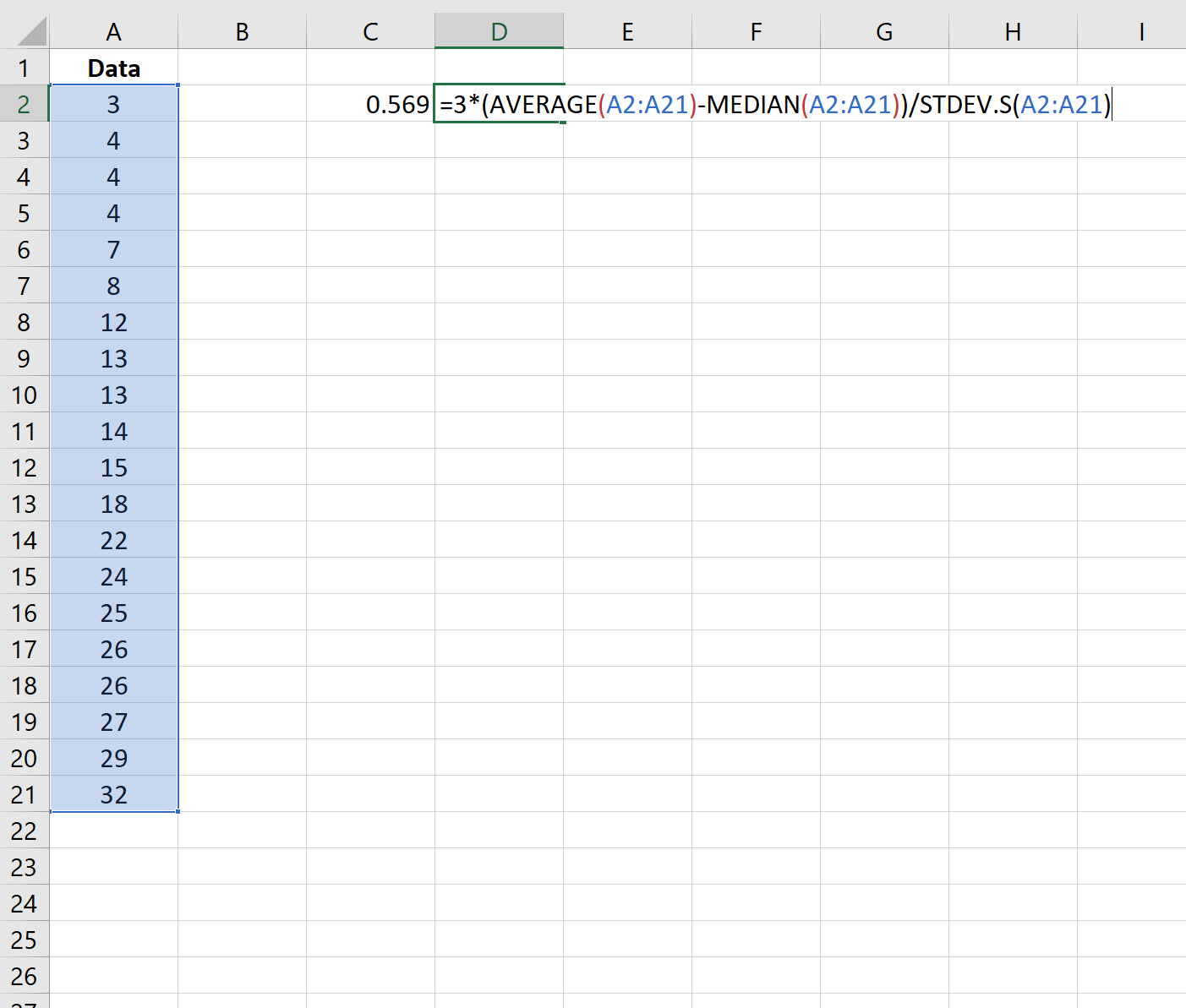
Асиметрія виявляється рівною 0,569 .

Як інтерпретувати асиметрію

Ми інтерпретуємо коефіцієнт асиметрії Пірсона наступним чином:

• Значення 0 означає відсутність асиметрії. Якби ми створили гістограму для візуалізації розподілу значень у наборі даних, вона була б ідеально симетричною.
• Додатне значення вказує на позитивний нахил або нахил «вправо». Гістограма виявить «хвіст» у правій частині розподілу.
• Від’ємне значення вказує на негативний нахил або нахил «ліворуч». Гістограма виявить «хвіст» у лівій частині розподілу.

У нашому попередньому прикладі асиметрія була позитивною, що вказує на те, що розподіл значень даних був позитивно спотвореним або «правильним».

Додаткові ресурси

Ознайомтеся з цією статтею , щоб отримати гарне пояснення лівого та правого викривлених розподілів.