Логарифмічна регресія в python (крок за кроком)
Логарифмічна регресія — це тип регресії, який використовується для моделювання ситуацій, у яких зростання або спад спочатку швидко прискорюється, а потім сповільнюється з часом.
Наприклад, наступний графік показує приклад логарифмічного розпаду:

Для такого типу ситуації зв’язок між змінною-прогностикою та змінною відповіді можна добре змоделювати за допомогою логарифмічної регресії.
Рівняння для моделі логарифмічної регресії має такий вигляд:
y = a + b*ln(x)
золото:
- y: змінна відповіді
- x: передбачувана змінна
- a, b: коефіцієнти регресії, які описують зв’язок між x і y
Наступний покроковий приклад показує, як виконати логарифмічну регресію в Python.
Крок 1: Створіть дані
Спочатку давайте створимо фальшиві дані для двох змінних: x і y :
import numpy as np x = np. arange (1, 16, 1) y = np. array ([59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5])
Крок 2: Візуалізуйте дані
Далі створимо швидку діаграму розсіювання, щоб візуалізувати зв’язок між x і y :
import matplotlib. pyplot as plt plt. scatter (x,y) plt. show ()
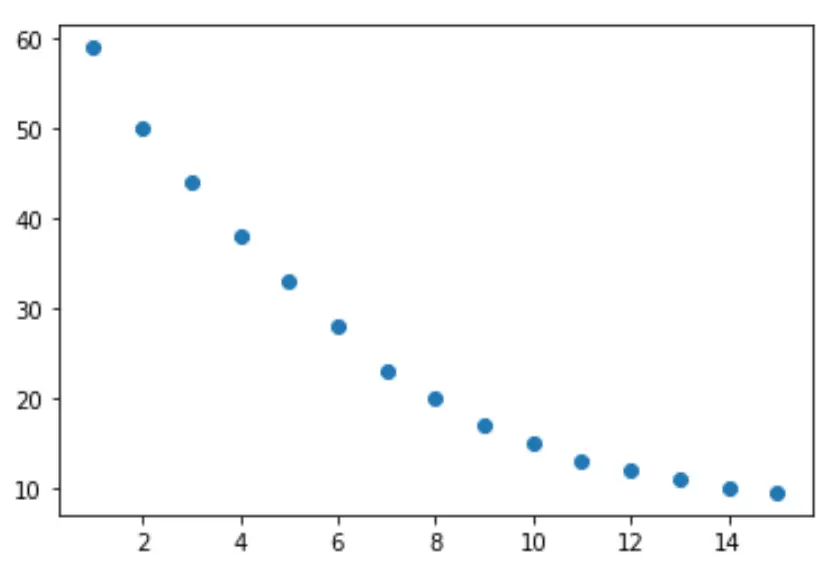
З графіка ми бачимо, що між двома змінними існує логарифмічний розпад. Значення змінної відповіді, y , спочатку швидко зменшується, а потім сповільнюється з часом.
Тому здається розумним підібрати рівняння логарифмічної регресії для опису зв’язку між змінними.
Крок 3: Підберіть модель логарифмічної регресії
Далі ми використаємо функцію polyfit() , щоб підібрати модель логарифмічної регресії, використовуючи натуральний логарифм від x як змінну-прогноз і y як змінну відповіді:
#fit the model fit = np. polyfit (np. log (x), y, 1) #view the output of the model print(fit) [-20.19869943 63.06859979]
Ми можемо використати коефіцієнти з результату, щоб написати наступне скориговане рівняння логарифмічної регресії:
y = 63,0686 – 20,1987 * ln(x)
Ми можемо використати це рівняння для прогнозування змінної відповіді y на основі значення змінної предиктора x . Наприклад, якщо x = 12, ми передбачимо, що y дорівнюватиме 12,87 :
y = 63,0686 – 20,1987 * ln(12) = 12,87
Бонус: не соромтеся використовувати цей онлайн-калькулятор логарифмічної регресії, щоб автоматично обчислити рівняння логарифмічної регресії для заданого предиктора та змінної відповіді.
Додаткові ресурси
Повний посібник із лінійної регресії в Python
Як виконати експоненціальну регресію в Python
Як виконати логістичну регресію в Python