R проти r-square: у чому різниця?

Два терміни, які студенти часто плутають у статистиці, це R і R-квадрат , які часто записують ^{як R2} .

У контексті простої лінійної регресії :

• A: Кореляція між змінною предиктора x і змінною відповіді y.
• R ² : Частка дисперсії у змінній відповіді, яку можна пояснити змінною предиктора в регресійній моделі.

А в контексті множинної лінійної регресії :

• A: Кореляція між спостережуваними значеннями змінної відповіді та прогнозованими значеннями змінної відповіді, зробленими моделлю.
• R ² : Частка дисперсії змінної відповіді, яку можна пояснити змінними предикторів регресійної моделі.

Зауважте, що значення R ² знаходиться між 0 і 1. Чим ближче значення до 1, тим сильніший зв’язок між змінною(ями) предиктора та змінною відповіді.

У наступних прикладах показано, як інтерпретувати значення R і R-квадрат у моделях простої лінійної регресії та лінійної регресії.

Приклад 1: Проста лінійна регресія

Припустімо, що ми маємо наступний набір даних, який показує кількість вивчених годин і результати іспитів, отримані 12 студентами в певному курсі математики:

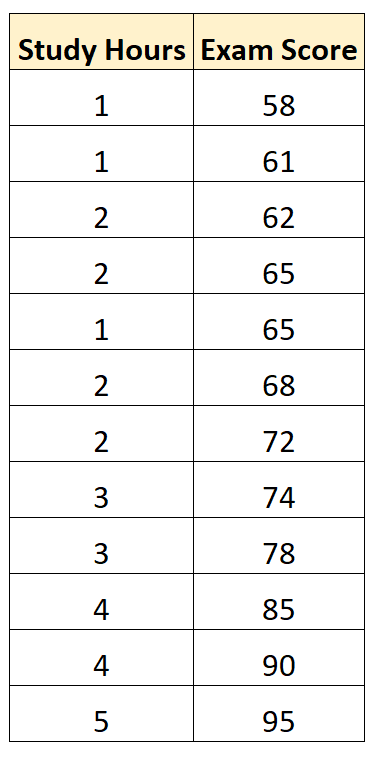
Використовуючи статистичне програмне забезпечення (як-от Excel, R, Python, SPSS тощо), ми можемо підібрати просту модель лінійної регресії, використовуючи «навчальні години» як змінну-прогноз і «оцінку за іспит» як змінну відповіді .

Ми можемо знайти наступний вихід для цієї моделі:

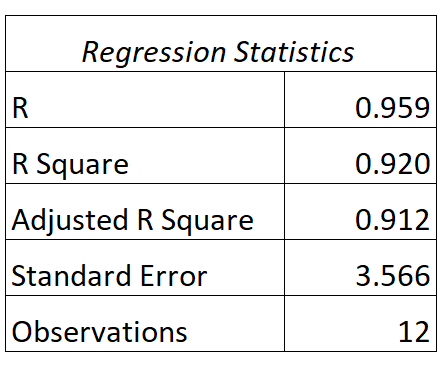
Ось як інтерпретувати квадратичні значення R і R цієї моделі:

• Відповідь: Співвідношення між вивченими годинами та результатом іспиту становить 0,959 .
• R ² : R у квадраті для цієї регресійної моделі становить 0,920 . Це говорить нам про те, що 92,0% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.

Також зауважте, що значення R ² просто дорівнює значенню R у квадраті:

^R2 = R * R = 0,959 * 0,959 = 0,920

Приклад 2: Множинна лінійна регресія

Припустімо, що ми маємо такий набір даних, який показує кількість вивчених годин, поточну оцінку студента та оцінку іспиту, отриману 12 студентами з певного курсу математики:

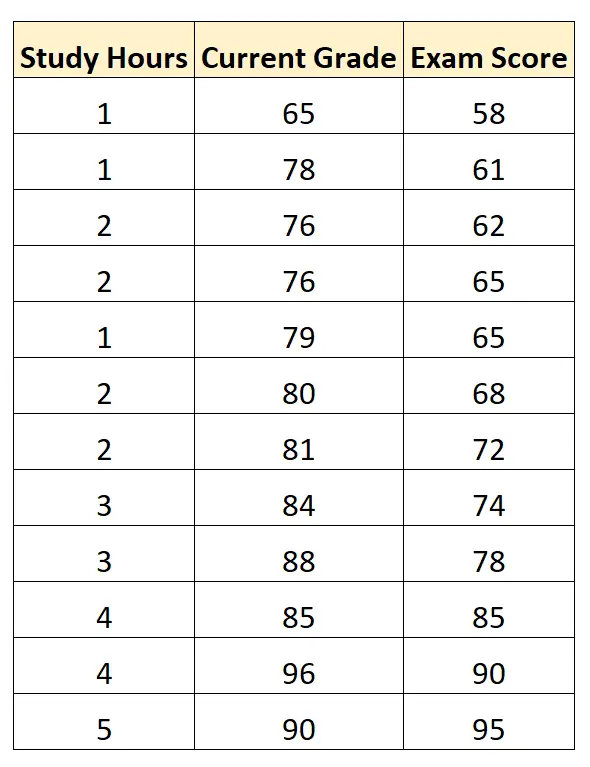
Використовуючи статистичне програмне забезпечення, ми можемо побудувати модель множинної лінійної регресії, використовуючи «навчальні години» та «поточну оцінку» як предикторні змінні та «екзаменаційну оцінку» як змінну відповіді.

Ми можемо знайти наступний вихід для цієї моделі:

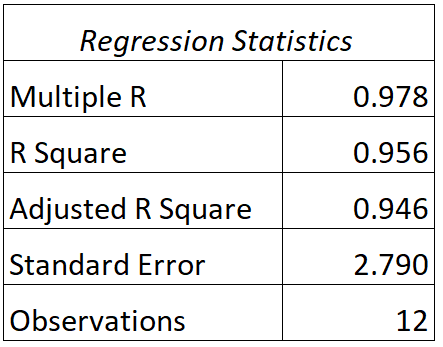
Ось як інтерпретувати квадратичні значення R і R цієї моделі:

• Відповідь: Кореляція між фактичними результатами тесту та прогнозованими результатами тесту моделі становить 0,978 .
• R ² : R у квадраті для цієї регресійної моделі становить 0,956 . Це говорить нам про те, що 95,6% варіації оцінок на іспитах можна пояснити кількістю вивчених годин і поточною оцінкою студента в класі.

Також зауважте, що значення R ² просто дорівнює значенню R у квадраті:

^R2 = R * R = 0,978 * 0,978 = 0,956

Додаткові ресурси

Що таке хороше значення R-квадрат?
Короткий посібник із суми квадратів: SST, SSR, SSE