Що таке монотонні відносини? (визначення + приклади)
У статистиці монотонний зв’язок між двома змінними відноситься до сценарію, в якому зміна однієї змінної зазвичай пов’язана зі зміною в певному напрямку іншої змінної.
Існує два типи монотонних зв’язків:
Позитивний монотонний: коли значення однієї змінної зростає, значення іншої змінної також має тенденцію до збільшення.
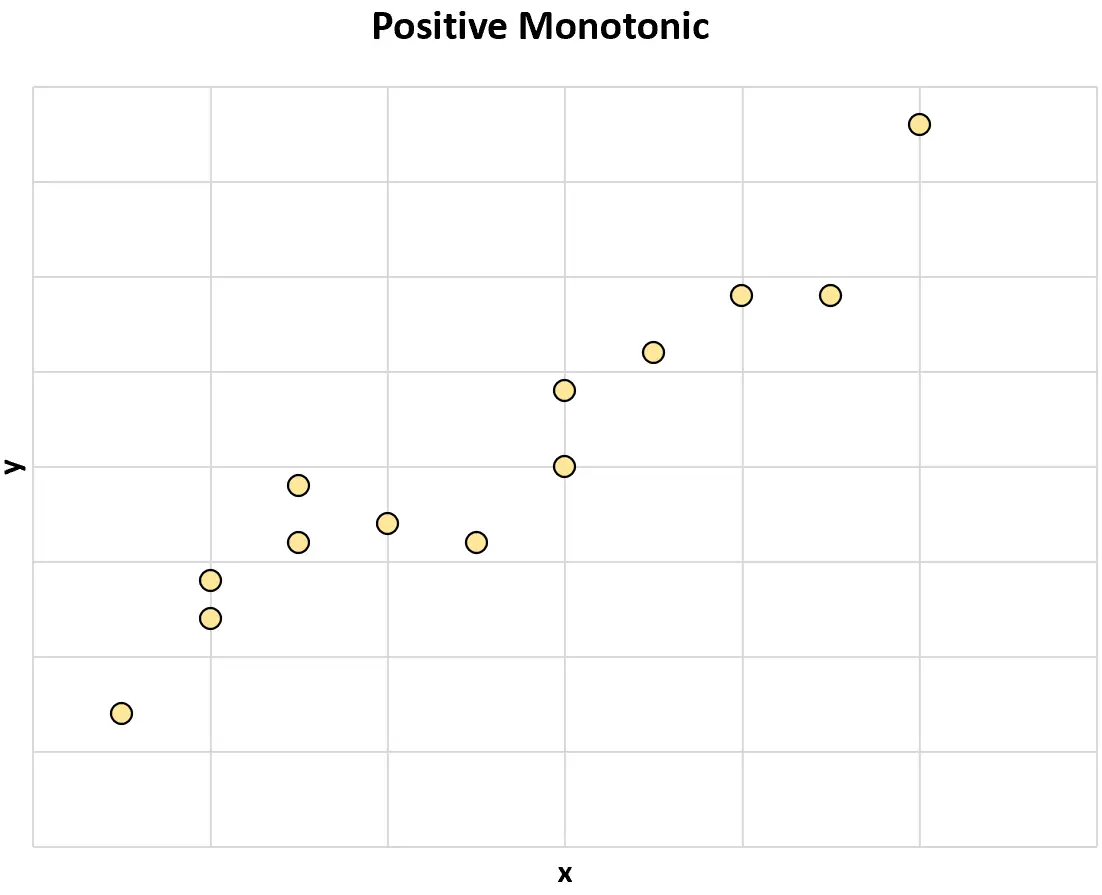
Негативний монотонний: коли значення однієї змінної зростає, значення іншої змінної має тенденцію до зменшення.
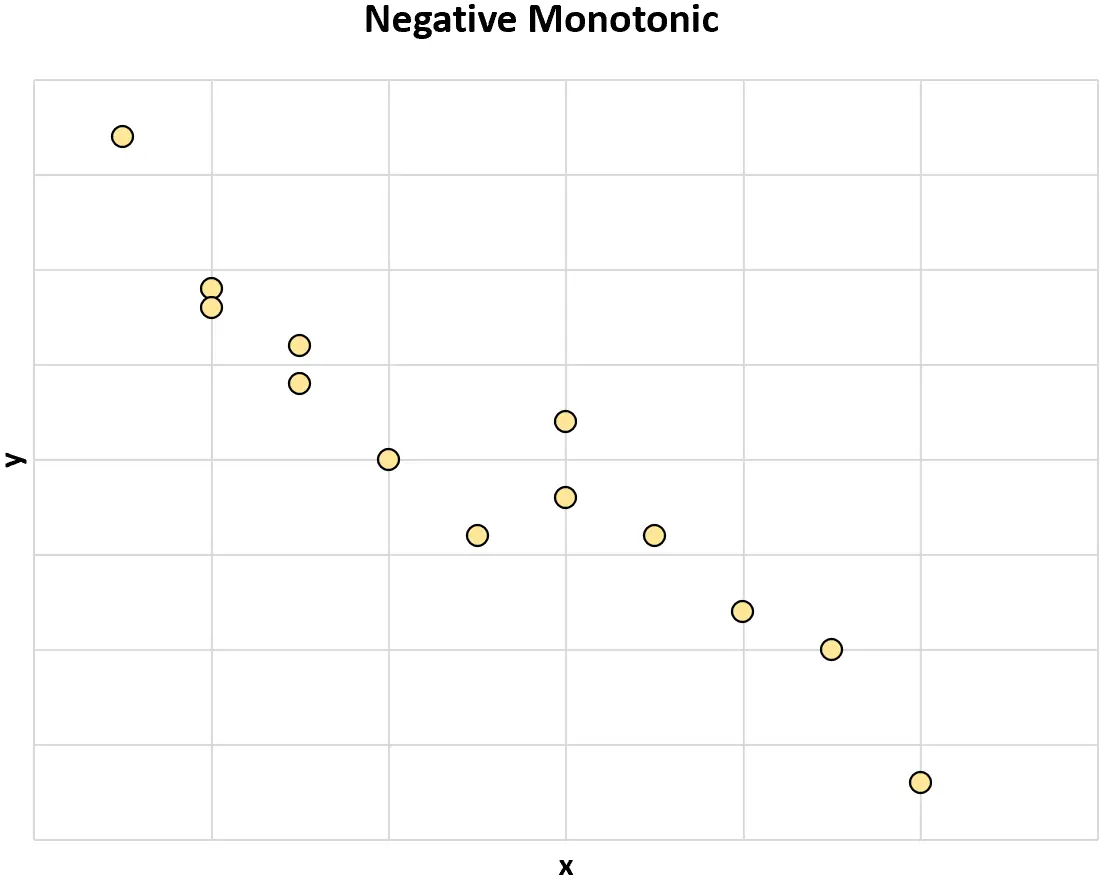
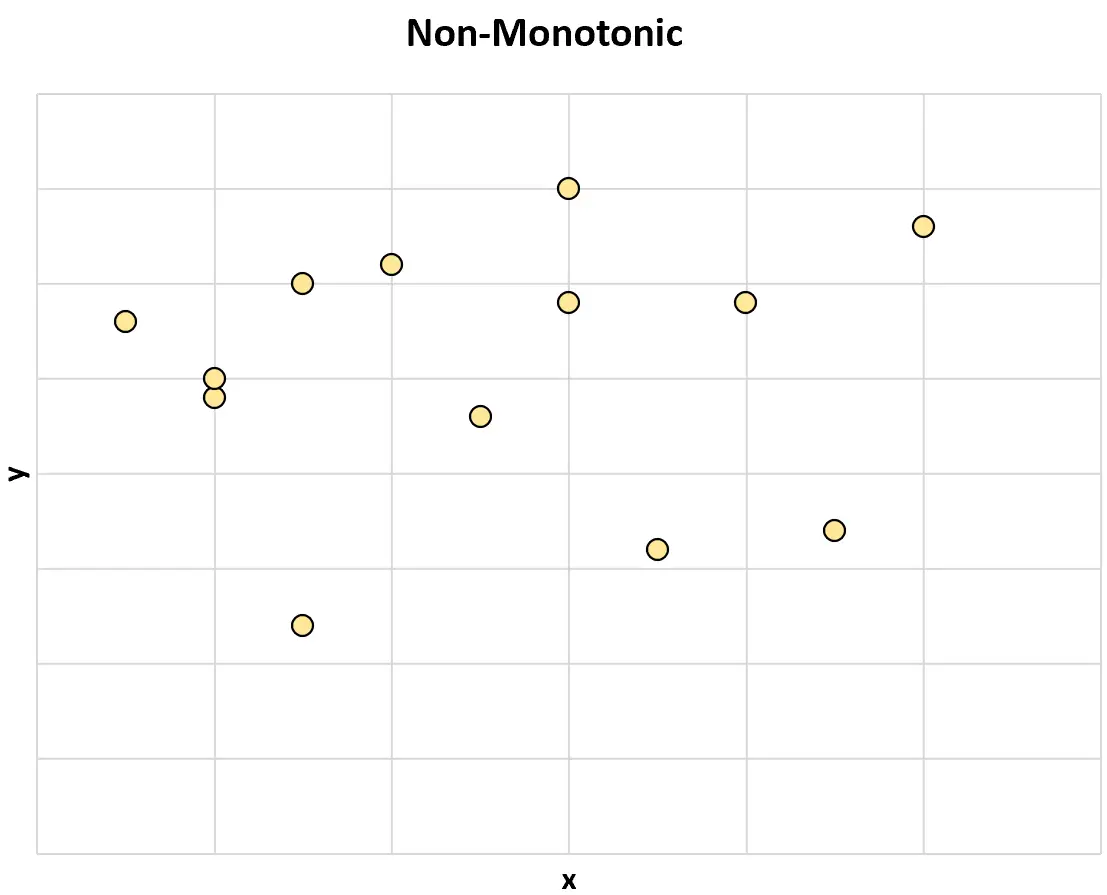
Якщо дві змінні зазвичай не змінюються в одному напрямку, то кажуть, що вони мають немонотонний зв’язок .
Ось приклад немонотонного зв’язку між двома змінними:
А ось ще один приклад немонотонного зв’язку між двома змінними:
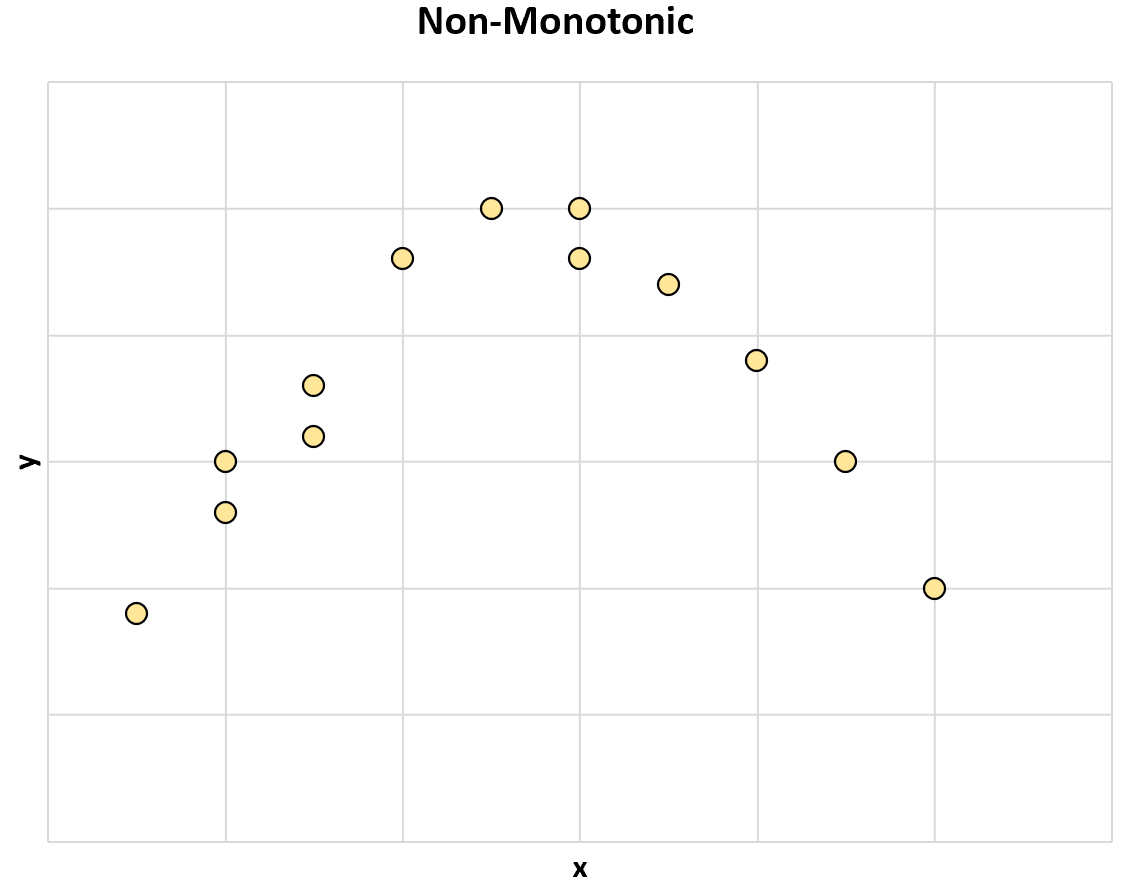
Коли значення x збільшується, значення y іноді збільшується, але іноді значення y зменшується .
Строго монотонний або не строго монотонний
Кажуть, що дві змінні мають суворо монотонний зв’язок, якщо зміни в одній змінній завжди пов’язані зі зміною в тому ж напрямку в іншій змінній.
Наприклад, наступний графік ілюструє суворо позитивний монотонний зв’язок між двома змінними:
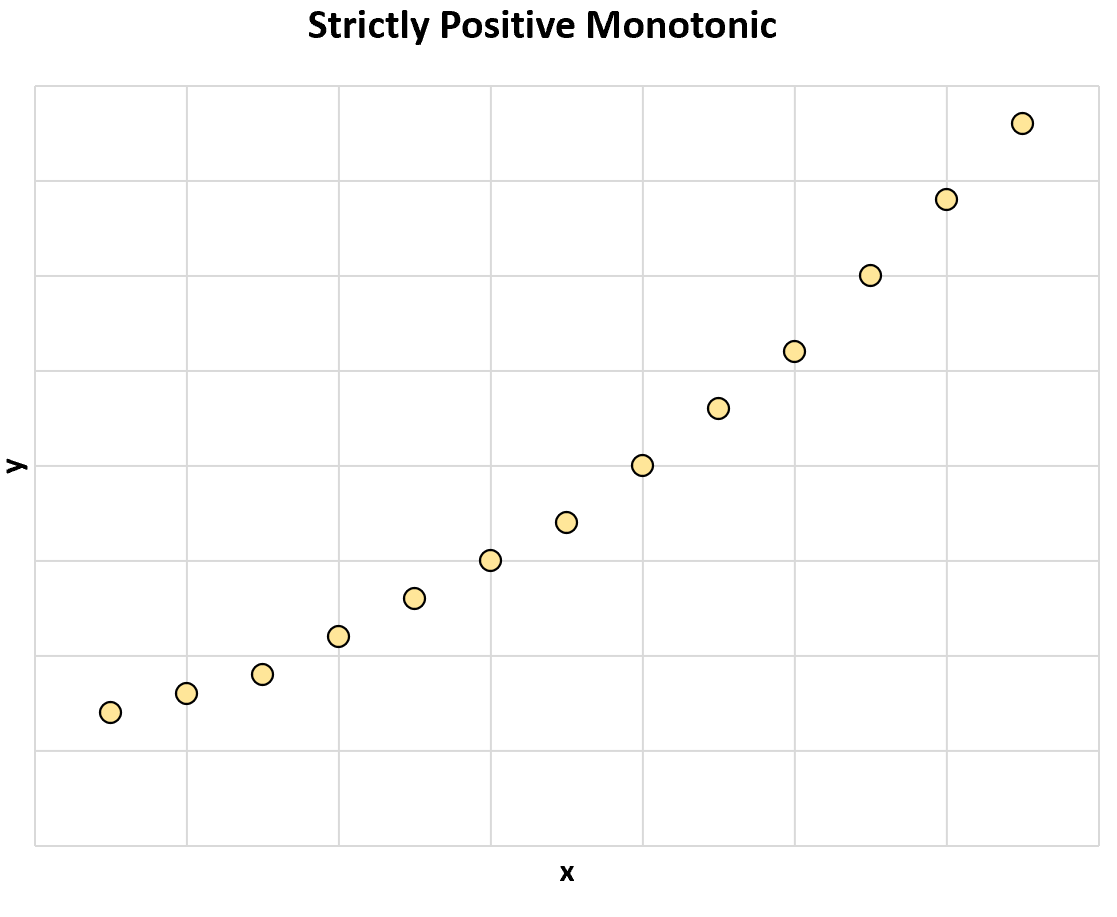
Зі збільшенням значення x значення y завжди зростає.
Наступний графік ілюструє суворо негативний монотонний зв’язок між двома змінними:
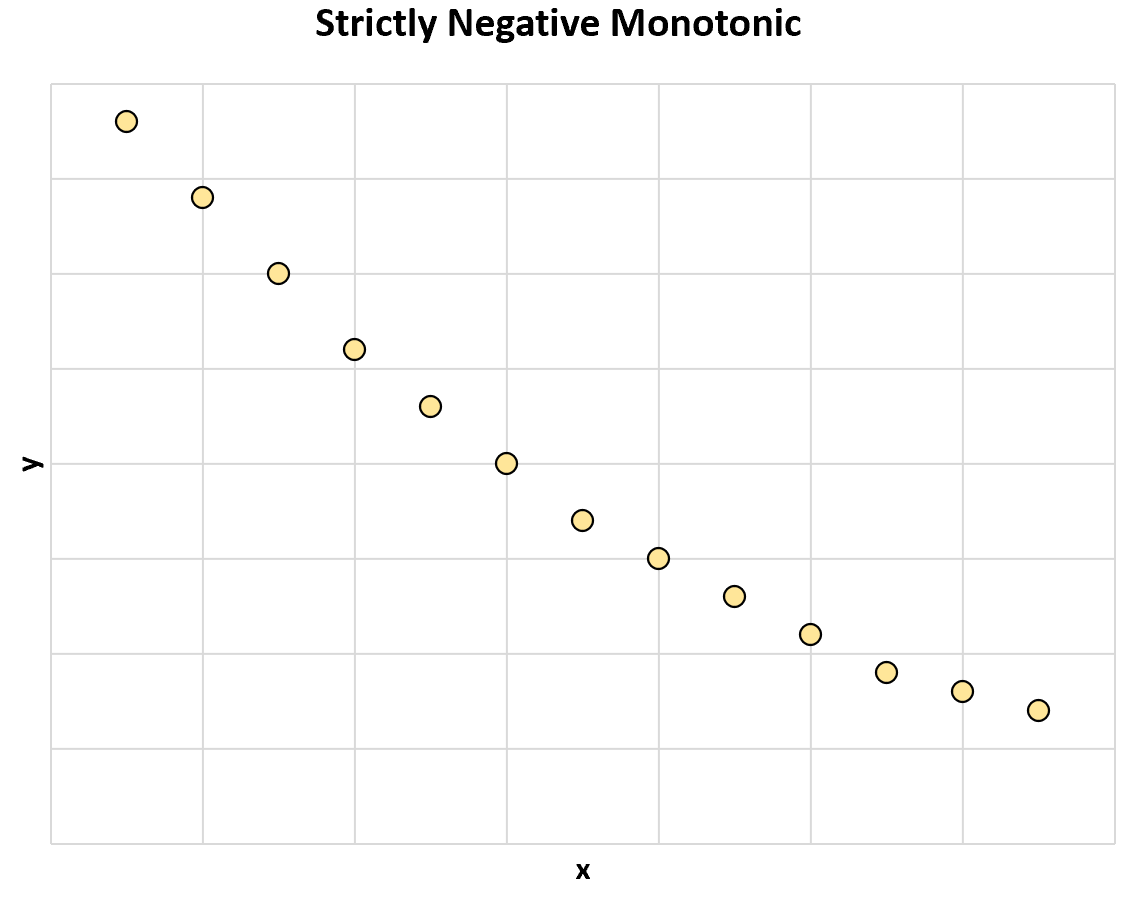
Зі збільшенням значення x значення y завжди зменшується.
Як кількісно визначити монотонні відносини
Найпоширенішим способом кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який вимірює лінійний зв’язок між двома змінними.
Цей коефіцієнт завжди приймає значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Чим ближче коефіцієнт до 1, тим сильніший позитивний зв’язок між двома змінними. І навпаки, чим ближчий коефіцієнт до -1, тим сильніший негативний зв’язок між двома змінними.
Однак, якщо зв’язок між двома змінними є монотонним, але нелінійним (як експоненціальний зв’язок), тоді доцільно використовувати кореляцію рангів Спірмена , яка була розроблена, щоб добре обробляти монотонні зв’язки.
Незалежно від того, який тип коефіцієнта кореляції ви обчислюєте, завжди доцільно створити діаграму розсіювання, щоб також візуалізувати зв’язок між змінними.