Коли слід використовувати кореляцію? (пояснення та приклади)

Кореляція використовується для вимірювання лінійного зв’язку між двома змінними.

Коефіцієнт кореляції завжди приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Питання, яке студенти часто задають: коли я повинен використовувати кореляцію?

Коротка відповідь: використовуйте кореляцію, коли потрібно кількісно визначити лінійний зв’язок між двома змінними, і жодна змінна не представляє змінну відповіді чи «результату» .

Наведені нижче приклади показують, коли слід і не слід використовувати кореляцію на практиці.

Приклад 1: Коли використовувати кореляцію

Припустімо, професор хоче зрозуміти лінійну залежність між результатами іспиту з математики та результатами іспиту з природничих наук студентів його класу.

Наприклад, чи студенти, які добре складають іспит з математики, також добре складають іспит з природничих наук? Або учні, які мають високі результати з математики, як правило, мають низькі результати з природничих наук?

У цьому сценарії він міг би обчислити кореляцію між балами іспиту з математики та балами іспиту з природничих наук, оскільки він просто хоче зрозуміти лінійний зв’язок між двома змінними, і жодна змінна не може вважатися змінною відповіді.

Припустимо, він обчислює коефіцієнт кореляції Пірсона і знаходить, що він дорівнює r = 0,78. Це сильна позитивна кореляція, яка означає, що учні, які мають хороші результати в математиці, також мають тенденцію добре працювати в науках.

Приклад 2: Коли не використовувати кореляцію

Скажімо, відділ маркетингу компанії хоче кількісно визначити вплив витрат на рекламу на загальний дохід.

Наприклад, на кожен додатковий долар, витрачений на рекламу, скільки додаткового доходу компанія може очікувати отримати?

У цьому сценарії відділ повинен використовувати модель лінійної регресії для кількісного визначення зв’язку між витратами на рекламу та загальним доходом, оскільки змінна «дохід» є змінною відповіді.

Припустімо, що відділ застосовує просту модель лінійної регресії та виявляє, що наступне рівняння найкраще описує зв’язок між витратами на рекламу та загальним доходом:

Загальний дохід = 145,4 + 0,34*(витрати на рекламу)

Ми б інтерпретували це так, що кожен додатковий долар, витрачений на рекламу, призводить до збільшення загального доходу в середньому на 0,34 долара.

Застереження щодо використання кореляції

Важливо зазначити, що кореляцію можна використовувати лише для кількісного визначення лінійного зв’язку між двома змінними.

Однак за певних обставин коефіцієнт кореляції не зможе ефективно охопити зв’язок між двома змінними, які мають нелінійний зв’язок.

Наприклад, припустімо, що ми створюємо таку діаграму розсіювання, щоб візуалізувати зв’язок між двома змінними:

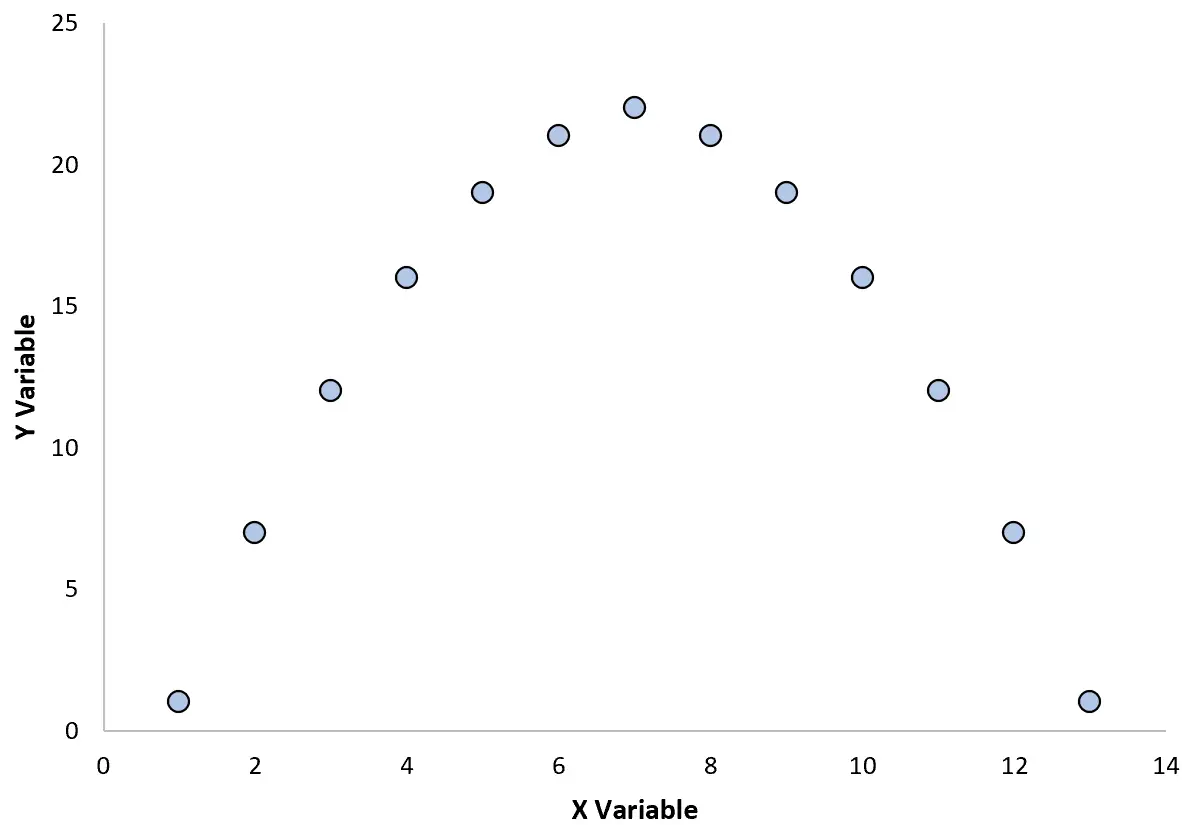
Якщо ми обчислимо коефіцієнт кореляції між цими двома змінними, то виявиться, що r = 0. Це означає, що між двома змінними немає лінійного зв’язку.

Проте з графіка ми бачимо, що дві змінні справді мають зв’язок – це просто квадратичне співвідношення, а не лінійне.

Отже, обчислюючи кореляцію між двома змінними, майте на увазі, що також може бути корисним створити діаграму розсіювання, щоб візуалізувати зв’язок між змінними.

Навіть якщо дві змінні не мають лінійного зв’язку, цілком можливо, що вони мають нелінійний зв’язок, який буде виявлено на діаграмі розсіювання.

Додаткові ресурси

У наступних посібниках докладніше пояснюється, як кореляція використовується в різних обставинах:

6 реальних прикладів кореляції
Що вважається «сильною» кореляцією?
Кореляція vs. асоціація: яка різниця?
Кореляція проти регресії: у чому різниця?