Логістична регресія проти лінійної регресії: основні відмінності

Дві моделі регресії, які найчастіше використовуються, це лінійна регресія та логістична регресія .

Обидва типи регресійних моделей використовуються для кількісного визначення зв’язку між однією або декількома змінними прогнозу та змінною відповіді , але між двома моделями є кілька ключових відмінностей:

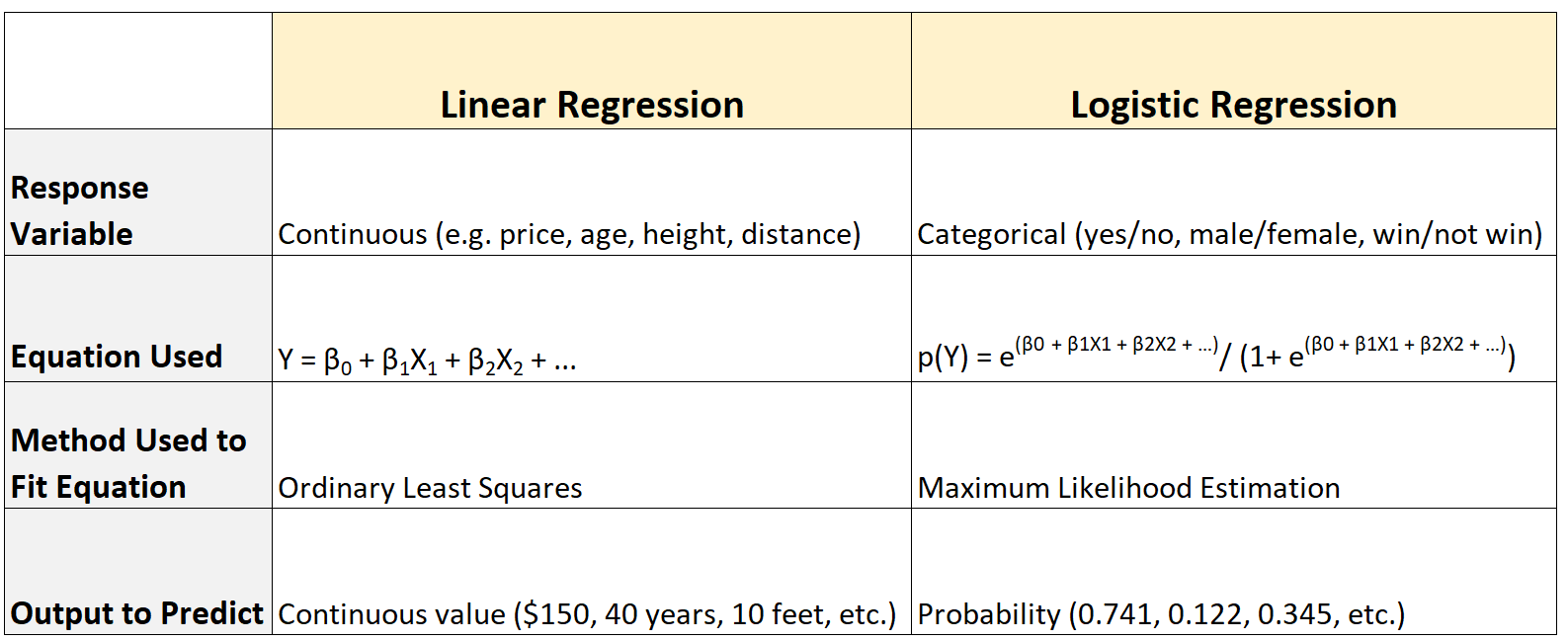
Ось короткий перелік відмінностей:

Відмінність №1: Тип змінної відповіді

Модель лінійної регресії використовується, коли змінна відповіді приймає безперервне значення таким чином, що:

• Ціна
• Висота
• Вік
• Відстань

І навпаки, модель логістичної регресії використовується, коли змінна відповіді приймає таке категоріальне значення, як:

• так або ні
• Чоловік чи жінка
• Виграти чи не виграти

Відмінність №2: використано рівняння

Лінійна регресія використовує таке рівняння, щоб узагальнити взаємозв’язок між змінною(ями) предиктора та змінною відповіді:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

золото:

• Y: змінна відповіді
• X _j : j- ^та прогнозна змінна
• β _j : середній вплив на Y від збільшення X _j на одну одиницю, утримуючи всі інші предиктори фіксованими

І навпаки, логістична регресія використовує таке рівняння:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Це рівняння використовується для прогнозування ймовірності того, що окреме спостереження потрапляє до певної категорії.

Відмінність №3: Метод, який використовується для підгонки рівняння

Лінійна регресія використовує метод, відомий як звичайні найменші квадрати, щоб знайти найкраще відповідне рівняння регресії.

І навпаки, логістична регресія використовує метод, відомий як оцінка максимальної правдоподібності, щоб знайти найкраще відповідне рівняння регресії.

Відмінність №4: прогнозований вихід

Лінійна регресія передбачає безперервне значення як вихід. Наприклад:

• Ціна ($150, $199, $400 тощо)
• Зріст (14 дюймів 2 фути 94,32 сантиметра тощо)
• Вік (2 місяці, 6 років, 41,5 років і т.д.)
• Відстань (1,23 милі, 4,5 кілометра тощо)

І навпаки, логістична регресія передбачає ймовірності як результат. Наприклад:

• 40,3% шансів бути прийнятим до університету.
• 93,2% шансів на перемогу в грі.
• Імовірність прийняття закону 34,2%.

Коли використовувати логістичну чи лінійну регресію

Наступні практичні завдання можуть допомогти вам краще зрозуміти, коли використовувати логістичну регресію чи лінійну регресію.

Проблема №1: Річний дохід

Припустімо, що економіст хоче використати змінні прогнозу (1) кількість відпрацьованих годин за тиждень і (2) роки навчання, щоб передбачити річний дохід окремих людей.

У цьому сценарії він використав би лінійну регресію , оскільки змінна відповіді (річний дохід) є безперервною.

Проблема №2: вступ до коледжу

Припустімо, що офіцер приймальної комісії коледжу хоче використати змінні прогнозу (1) GPA та (2) бал ACT, щоб передбачити ймовірність того, що студента приймуть до певного університету.

У цьому сценарії вона використала б логістичну регресію , оскільки змінна відповіді є категоричною і може приймати лише два значення: приймається чи не приймається.

Проблема №3: Ціни на нерухомість

Припустімо, що агент з нерухомості хоче використати змінні прогнозу (1) квадратні метри, (2) кількість спалень і (3) кількість ванних кімнат, щоб передбачити ціни продажу будинку.

У цьому сценарії вона використала б лінійну регресію , оскільки змінна відповіді (ціна) є постійною.

Проблема №4: Виявлення спаму

Припустімо, комп’ютерний програміст хоче використати змінні предиктора (1) кількість слів і (2) країну походження, щоб передбачити ймовірність того, що даний електронний лист є спамом.

У цьому сценарії використовуватиметься логістична регресія , оскільки змінна відповіді є категоричною та може приймати лише два значення: спам або не спам.

Додаткові ресурси

Наступні навчальні посібники пропонують більше деталей про лінійну регресію:

• Вступ до простої лінійної регресії
• Вступ до множинної лінійної регресії
• 4 приклади використання лінійної регресії в реальному житті

Наступні навчальні посібники пропонують більше деталей про логістичну регресію:

• Вступ до логістичної регресії
• 4 приклади використання логістичної регресії в реальному житті