Як обчислити дисперсію розподілу ймовірностей
Розподіл ймовірностей говорить нам про ймовірність того, що випадкова величина набуває певних значень.
Наприклад, наступний розподіл ймовірностей говорить нам про ймовірність того, що певна футбольна команда заб’є певну кількість голів у даному матчі:

Щоб знайти дисперсію розподілу ймовірностей, ми можемо використати таку формулу:
σ 2 = Σ(x i -μ) 2 * P(x i )
золото:
- x i : i-те значення
- μ: середнє значення розподілу
- P(x i ): ймовірність i-го значення
Наприклад, розглянемо наш розподіл ймовірностей для футбольної команди:

Середня кількість голів футбольної команди розраховується наступним чином:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гол.
Тоді ми могли б обчислити дисперсію наступним чином:
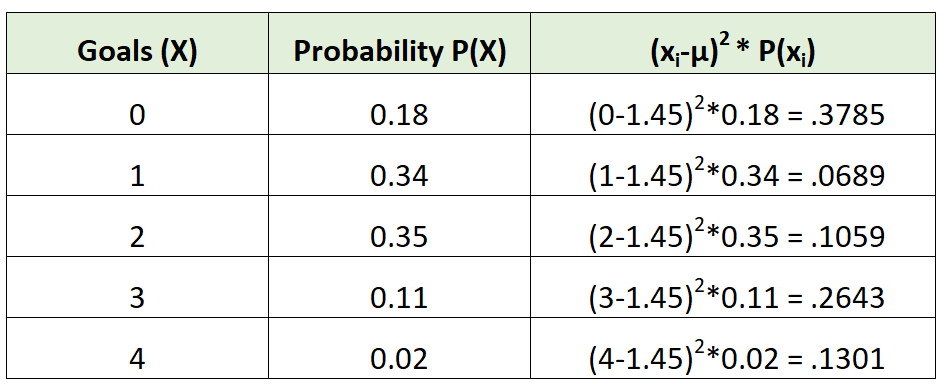
Дисперсія – це просто сума значень у третьому стовпці. Отже, ми б обчислили його таким чином:
σ2 = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475
У наведених нижче прикладах показано, як обчислити дисперсію розподілу ймовірностей у кількох інших сценаріях.
Приклад 1: Різниця в поломках транспортних засобів
Наступний розподіл ймовірностей говорить нам про ймовірність того, що даний автомобіль зазнає певної кількості відмов акумулятора протягом 10-річного періоду:
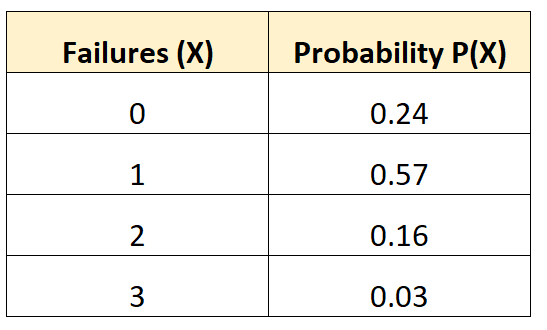
Щоб знайти дисперсію цього розподілу ймовірностей, нам спочатку потрібно обчислити середню кількість очікуваних відмов:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 відмов.
Тоді ми могли б обчислити дисперсію наступним чином:
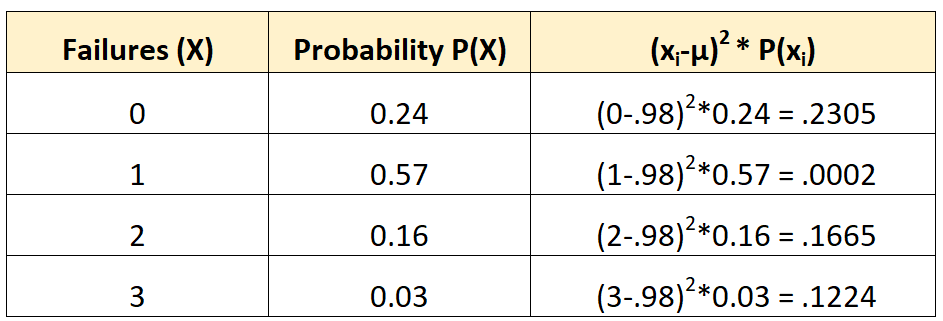
Дисперсія – це сума значень у третьому стовпці. Отже, ми б обчислили його таким чином:
σ2 = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196
Приклад 2: Варіація продажів
Наступний розподіл ймовірностей говорить нам про ймовірність того, що даний продавець зробить певну кількість продажів у наступному місяці:
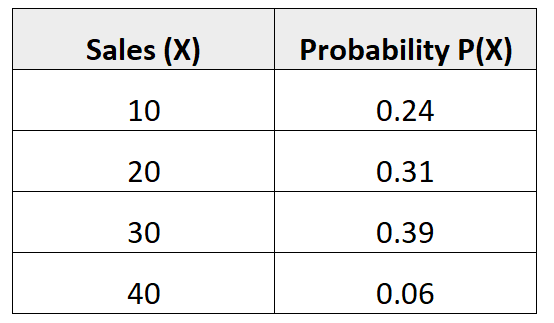
Щоб знайти дисперсію цього розподілу ймовірностей, нам спочатку потрібно обчислити середню кількість очікуваних продажів:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 брудних.
Тоді ми могли б обчислити дисперсію наступним чином:
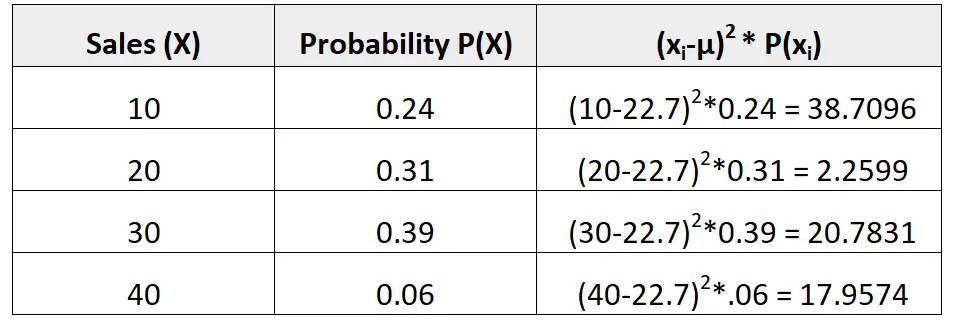
Дисперсія – це сума значень у третьому стовпці. Отже, ми б обчислили його таким чином:
σ2 = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71
Зверніть увагу, що ми також можемо використовувати калькулятор розподілу ймовірностей для автоматичного обчислення дисперсії цього розподілу:
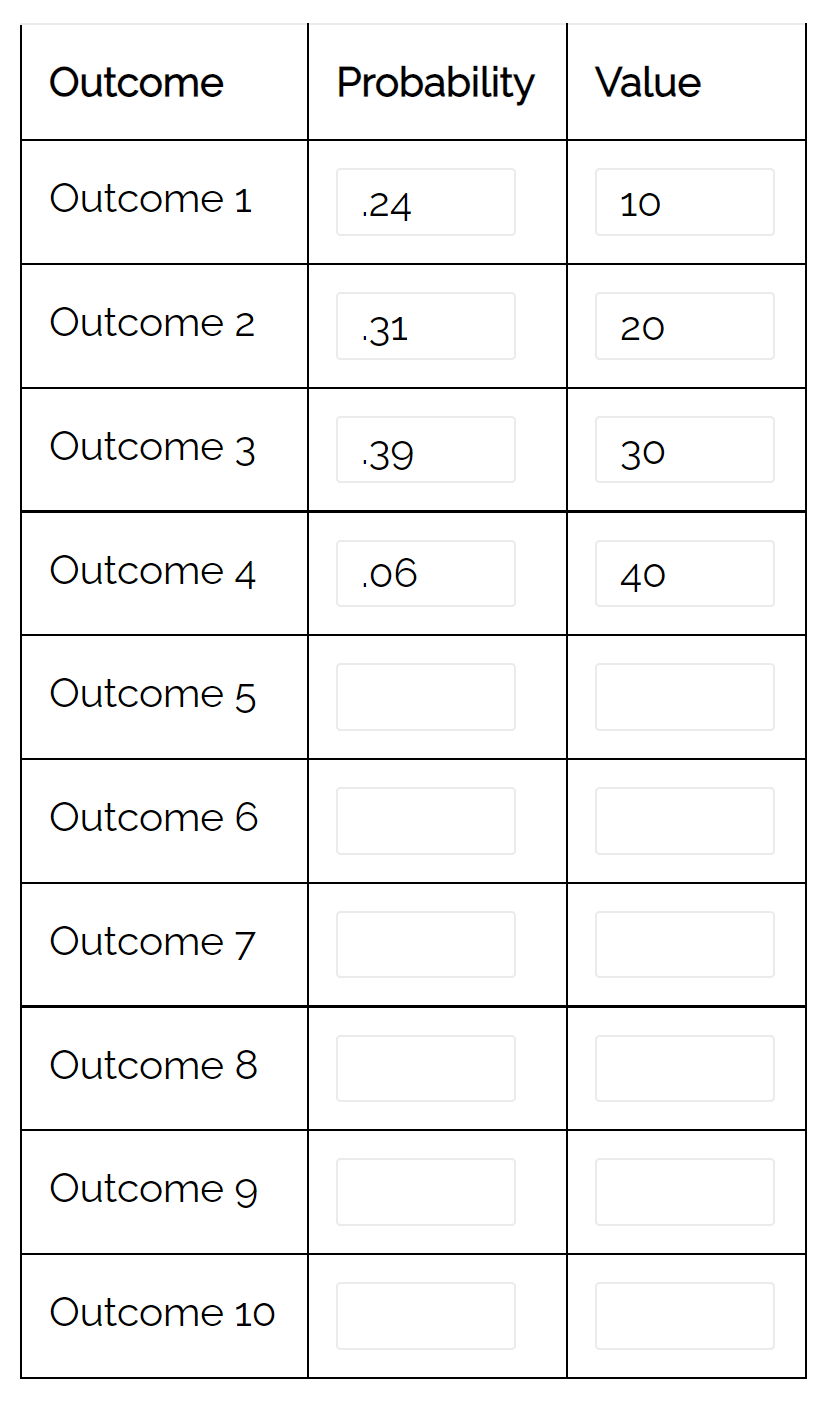

Різниця 79,71 . Це відповідає значенню, яке ми розрахували вручну.