Інтерполяція чи екстраполяція: в чому різниця?

Два терміни, які студенти часто плутають у статистиці, це інтерполяція та екстраполяція .

Ось різниця:

Інтерполяція стосується прогнозування значень, які потрапляють у діапазон точок даних.

Екстраполяція стосується прогнозування значень, які виходять за межі діапазону точок даних.

Наступний приклад ілюструє різницю між двома термінами.

Приклад: інтерполяція та екстраполяція

Припустимо, що ми маємо наступний набір даних:

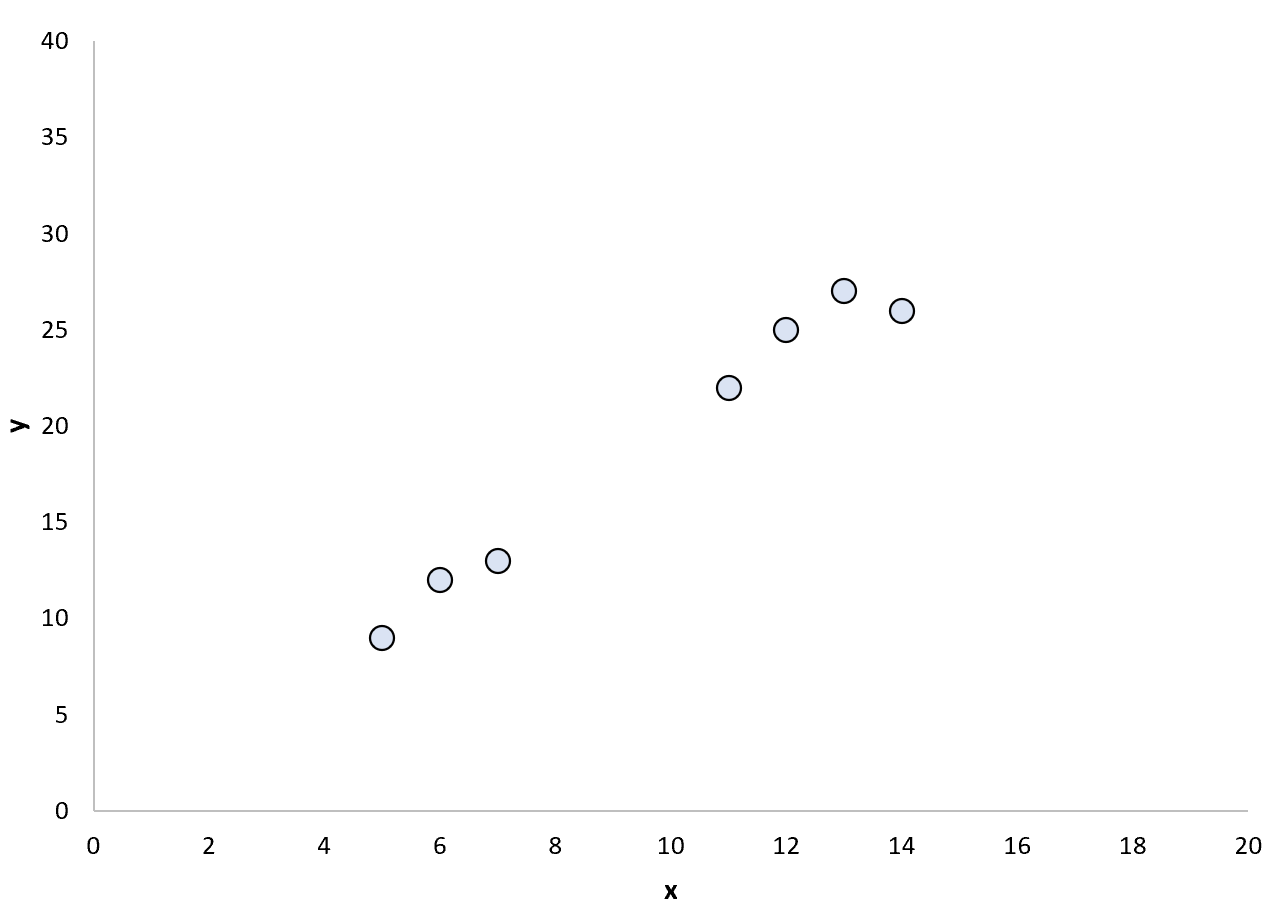
Ми можемо вирішити підібрати просту модель лінійної регресії до цих точок:

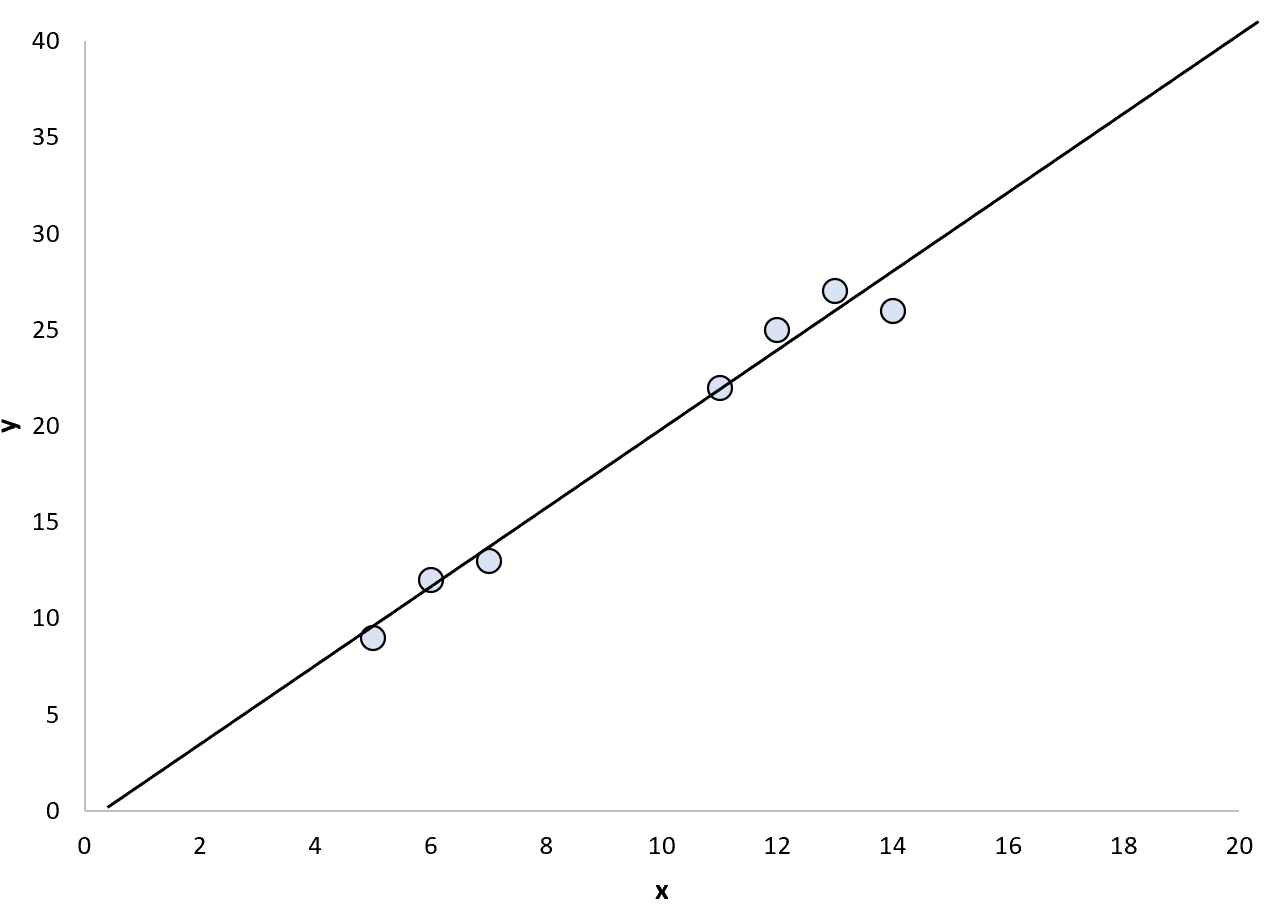
Тоді ми могли б використовувати підігнану регресійну модель для прогнозування точкових значень як усередині , так і за межами діапазону точок даних.

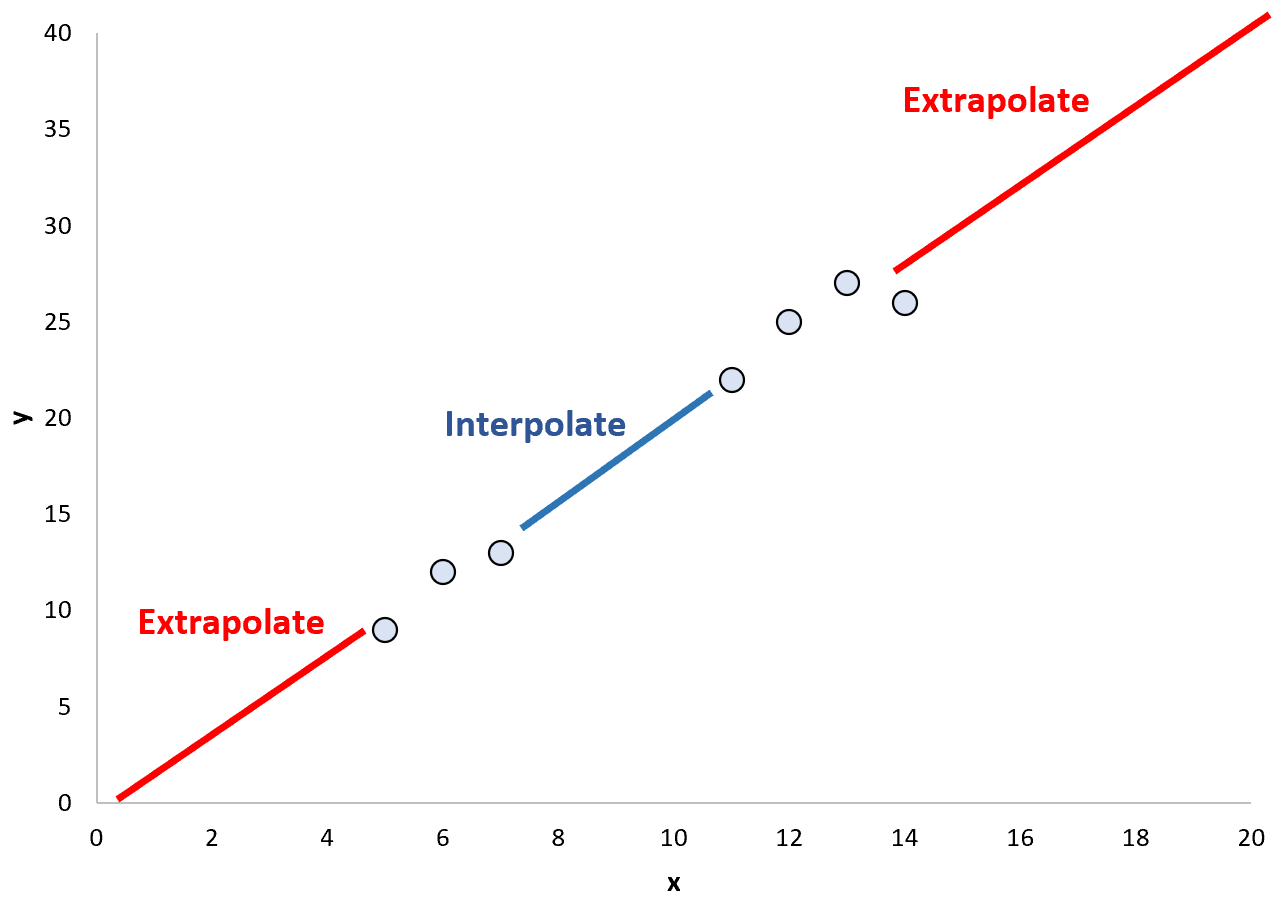
Коли ми використовуємо підігнану регресійну модель для прогнозування точкових значень у межах існуючого діапазону точок даних, це називається інтерполяцією.

І навпаки, коли ми використовуємо підігнану модель регресії для прогнозування точкових значень за межами існуючого діапазону, це називається екстраполяцією :

Потенційна небезпека екстраполяції

Під час екстраполяції ми припускаємо, що той самий шаблон, який існує всередині поточного діапазону точок даних, також існує поза діапазоном.

Однак це може бути небезпечним припущенням, оскільки цілком можливо, що шаблон, який існує за межами поточного діапазону точок даних, дуже відрізняється:

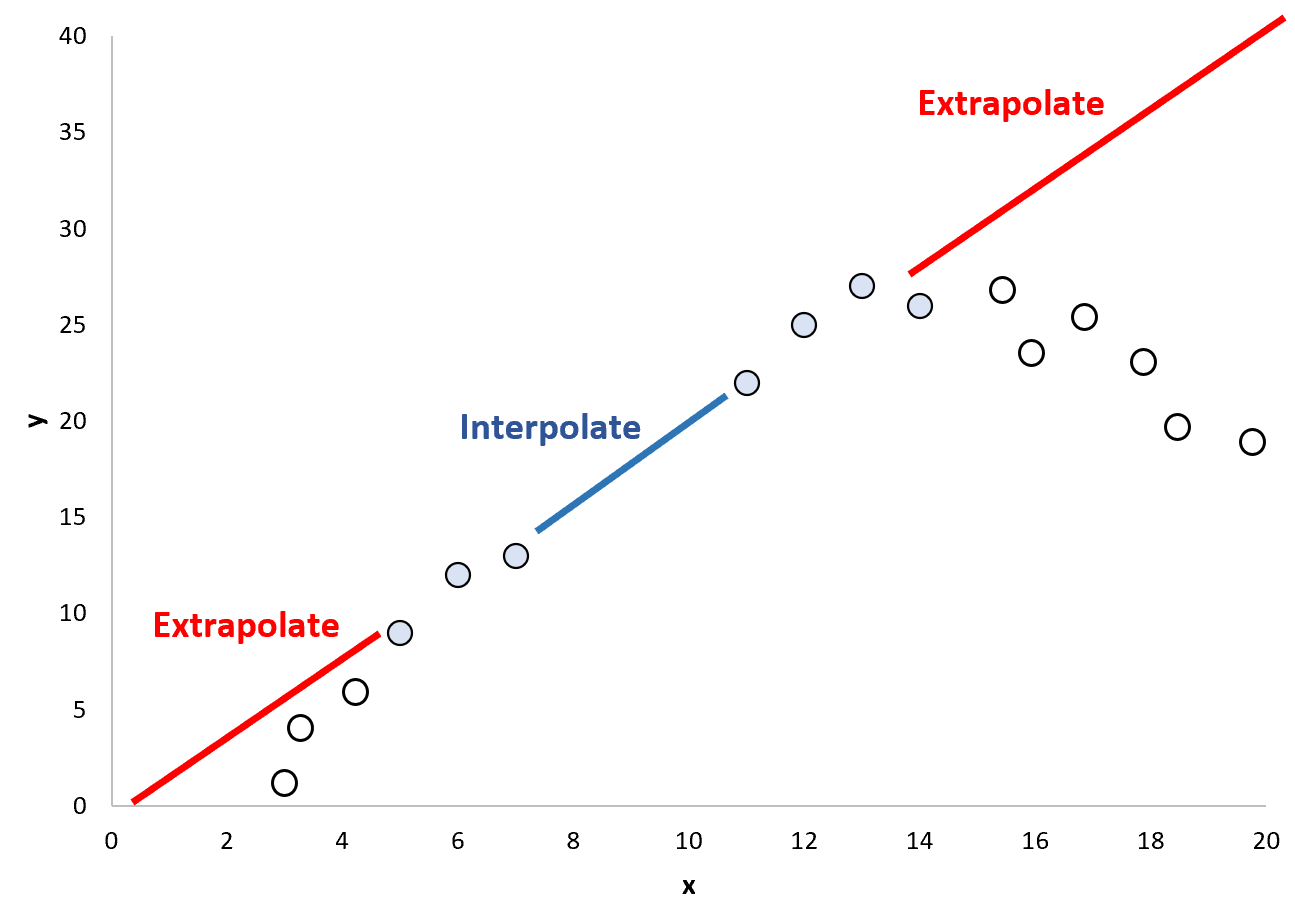
З цієї причини може бути небезпечно використовувати екстраполяцію для прогнозування значень точок даних, які виходять за межі діапазону значень, що використовуються для створення регресійної моделі.

На практиці часто має сенс використовувати екстраполяцію для прогнозування точкових значень, які трохи виходять за межі діапазону існуючих значень, але чим далі від діапазону, тим більша ймовірність того, що різниця між прогнозованим значенням і фактичним значенням цінність важлива. .

Коли використовувати екстраполяцію

Щоб визначити, чи є екстраполяція розумною ідеєю, часто потрібен досвід у певній галузі.

Наприклад, припустімо, що відділ маркетингу компанії застосовує просту модель лінійної регресії, використовуючи витрати на рекламу як змінну прогнозу та загальний дохід як змінну відповіді.

У цьому сценарії може бути розумним припустити, що постійне збільшення витрат на рекламу призведе до прогнозованого збільшення загального доходу:

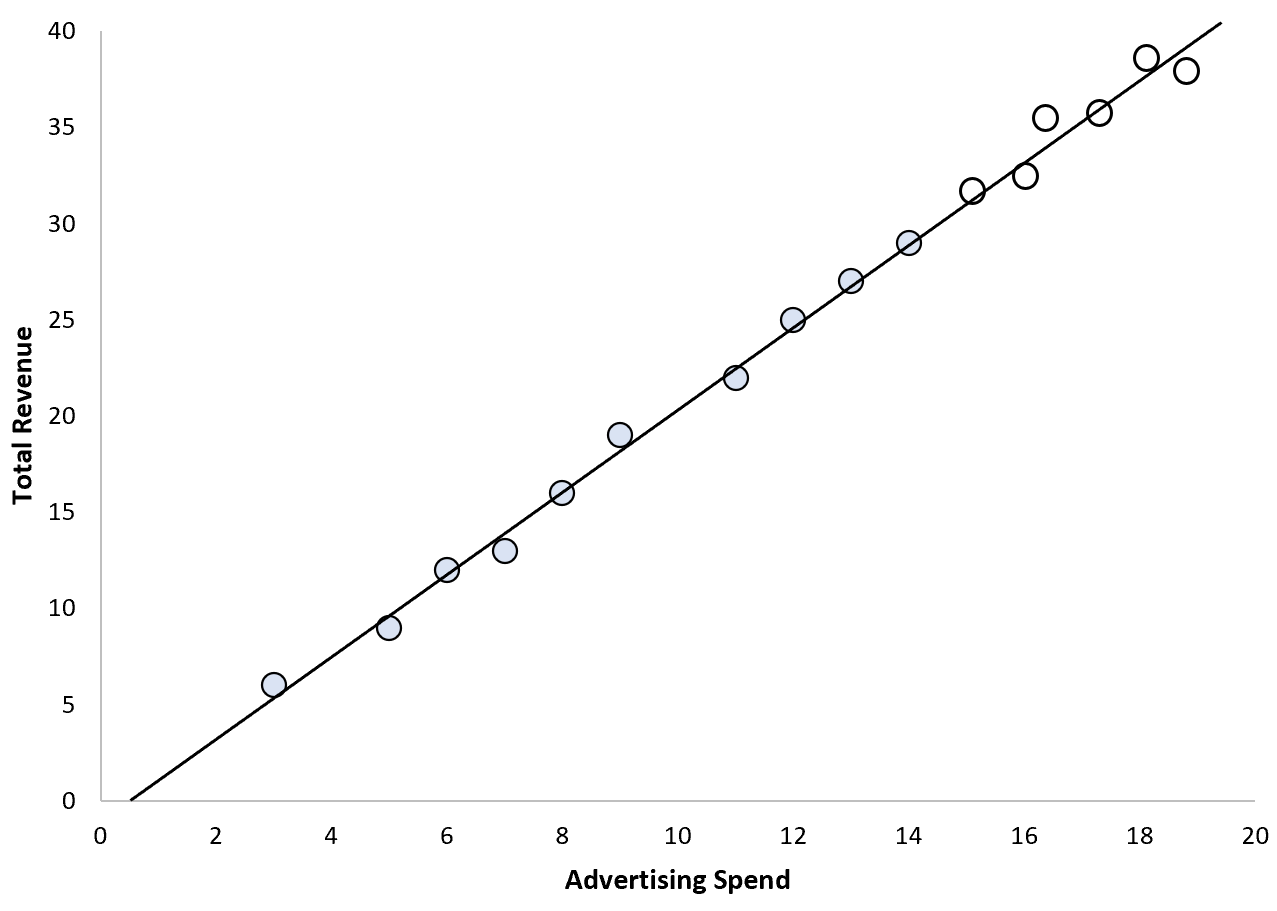
У цьому сценарії ми можемо бути цілком впевнені в своїй здатності екстраполювати значення.

Однак розглянемо сценарій, за якого біолог хоче використовувати загальне добриво для прогнозування росту рослин.

Вона може вирішити підібрати просту модель лінійної регресії до точок даних, але оскільки існує верхня межа висоти рослини, ймовірно, немає сенсу використовувати екстраполяцію для прогнозування точкових значень. поза діапазоном значень. значення, які використовуються для відповідності моделі:

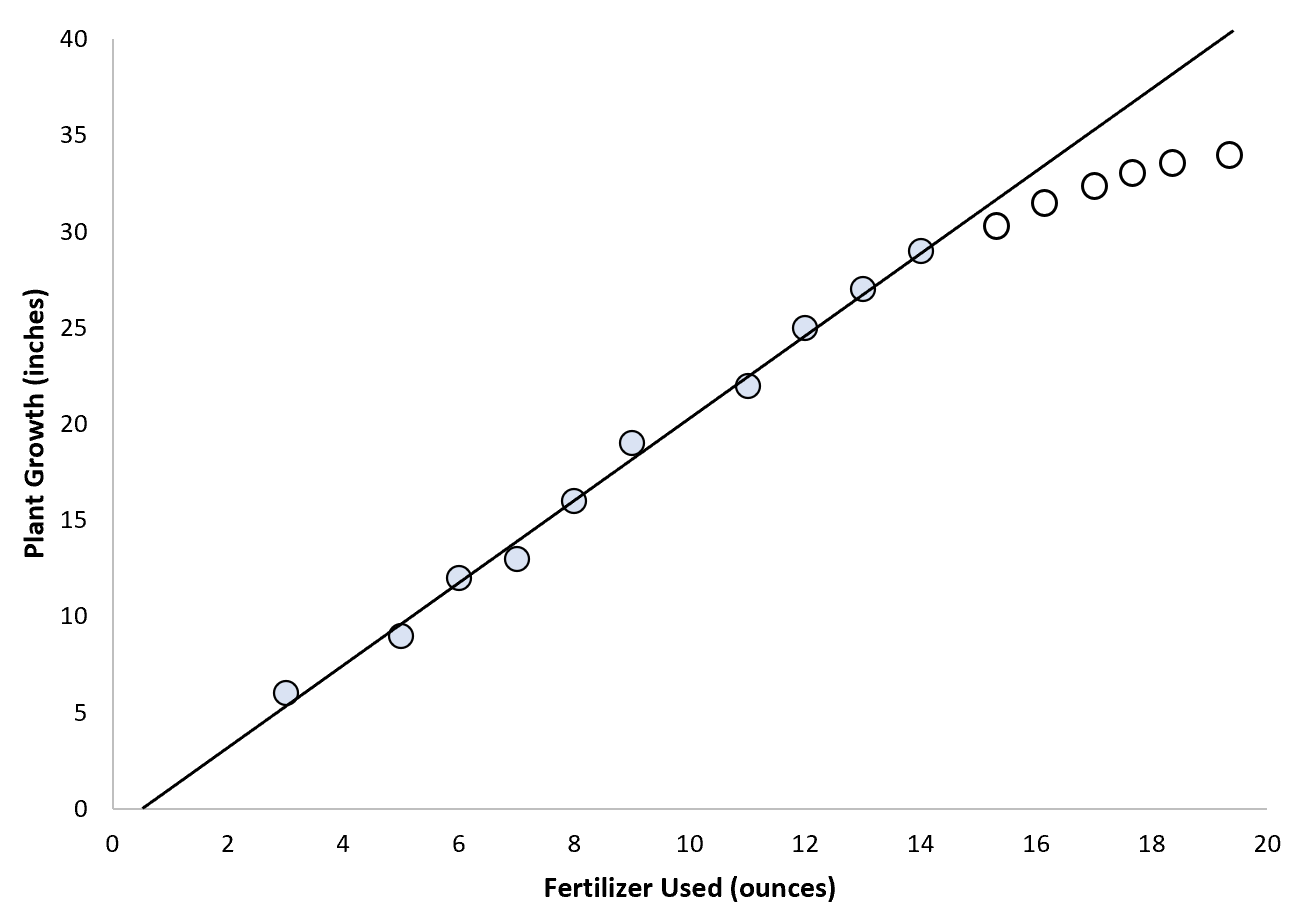
У цьому сценарії ми можемо мати набагато менше впевненості в нашій здатності екстраполювати значення.

Висновок : екстраполяція може мати більше сенсу в деяких областях, ніж в інших, але завжди існує потенційна небезпека, що модель, яка існує в діапазоні значень, які використовуються для підгонки моделі, не існує за межами пляжу.

Додаткові ресурси

Як виконати лінійну інтерполяцію в Excel
Як робити прогнози за допомогою лінійної регресії