Як використовувати розподіл t у python

Розподіл t — це розподіл ймовірностей, подібний до нормального розподілу , за винятком того, що він має більші «хвости», ніж нормальний розподіл.

Іншими словами, більше значень у розподілі розташовано на кінцях, ніж у центрі порівняно з нормальним розподілом:

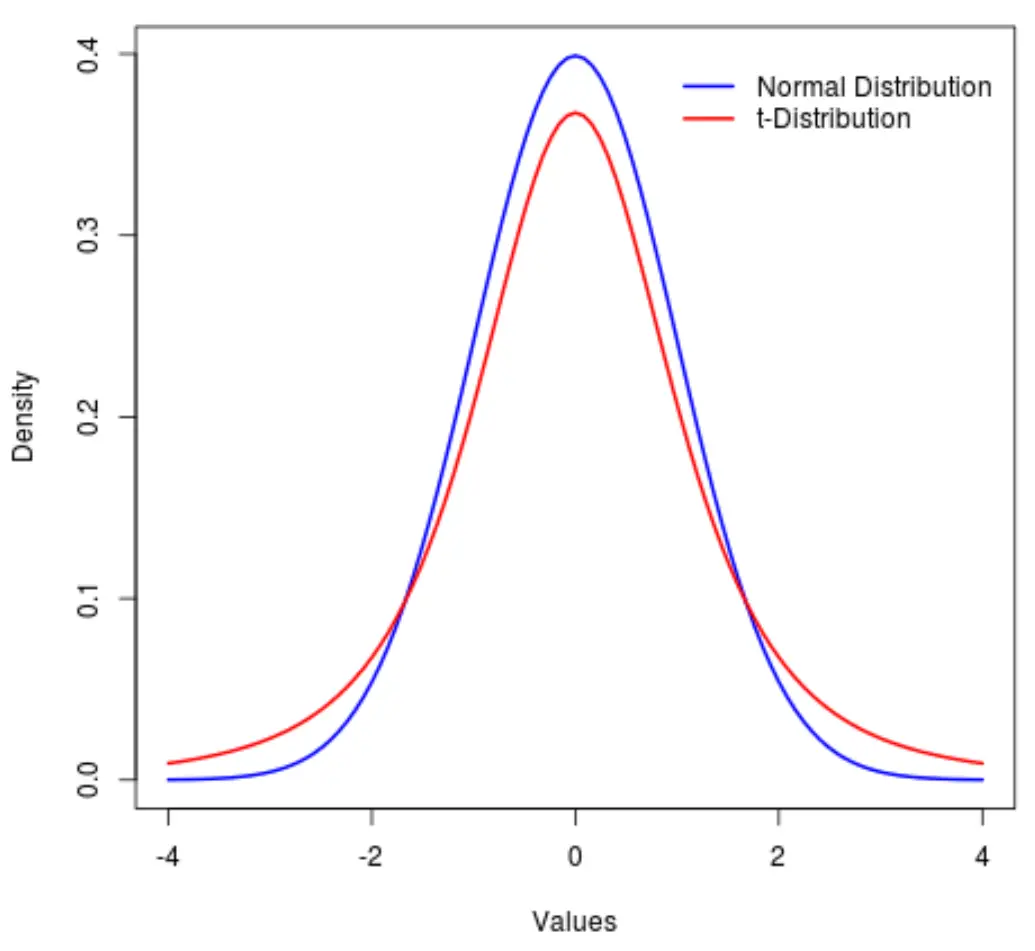
Цей посібник пояснює, як використовувати дистрибутив t у Python.

Як створити для розповсюдження

Ви можете використовувати функцію t.rvs(df, size) , щоб генерувати випадкові значення з розподілу з певними ступенями свободи та розміром вибірки:

 from scipy. stats import t

#generate random values from t distribution with df=6 and sample size=10
t. rvs (df= 6 , size= 10 )

array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611,
       -0.45384974, -0.2767931, -0.40177789, -0.3602592, 0.38262431])

Результатом є таблиця з 10 значень, які йдуть одне за одним відповідно до розподілу з 6 ступенями свободи.

Як розрахувати значення P за допомогою розподілу t

Ми можемо використати функцію t.cdf(x, df, loc=0, scale=1) , щоб знайти p-значення, пов’язане зі статистикою t-тесту.

Приклад 1: визначення одностороннього P-значення

Припустімо, ми виконуємо односторонню перевірку гіпотези та отримуємо тестову статистику -1,5 і ступені свободи = 10 .

Ми можемо використати наступний синтаксис, щоб обчислити p-значення, яке відповідає цій тестовій статистиці:

 from scipy. stats import t

#calculate p-value
t. cdf (x=-1.5, df=10)

0.08225366322272008

Одностороннє значення p, яке відповідає тестовій статистиці -1,5 з 10 ступенями свободи, становить 0,0822 .

Приклад 2: визначення двостороннього P-значення

Припустімо, що ми виконуємо двосторонню перевірку гіпотез і отримуємо тестову статистику 2,14 і ступені свободи = 20 .

Ми можемо використати наступний синтаксис, щоб обчислити p-значення, яке відповідає цій тестовій статистиці:

 from scipy. stats import t

#calculate p-value
(1 - t. cdf (x=2.14, df=20)) * 2

0.04486555082549959

Двостороннє значення p, яке відповідає тестовій статистиці 2,14 із 20 ступенями свободи, становить 0,0448 .

Примітка : Ви можете перевірити ці відповіді за допомогою калькулятора зворотного t-розподілу.

Як відстежити розподіл

Ви можете використовувати наступний синтаксис, щоб побудувати графік розподілу з певними ступенями свободи:

 from scipy. stats import t
import matplotlib. pyplot as plt

#generate t distribution with sample size 10000
x = t. rvs (df= 12 , size= 10000 )

#create plot of t distribution
plt. hist (x, density= True , edgecolor=' black ', bins= 20 )

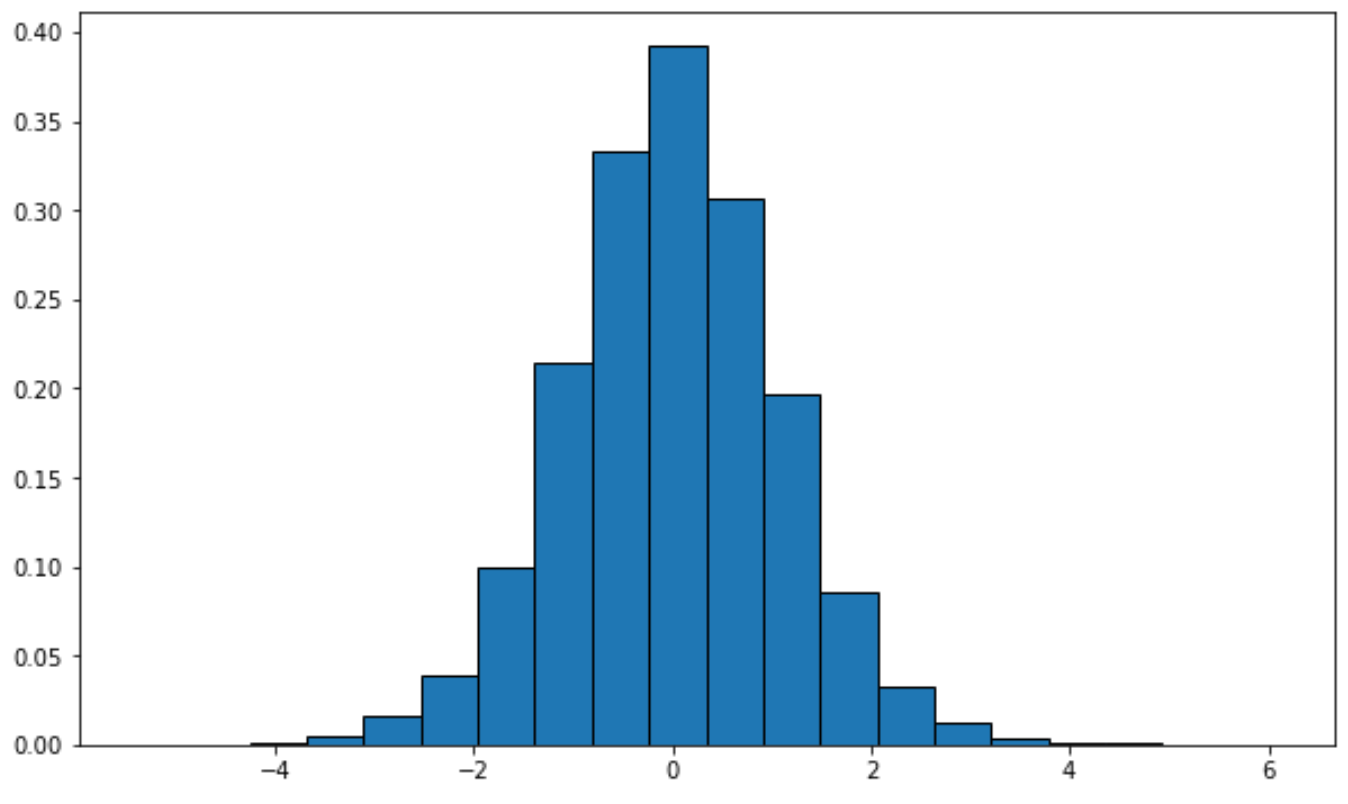
Крім того, ви можете створити криву щільності за допомогою пакета візуалізації seaborn :

 import seaborn as sns

#create density curve
sns. kdeplot (x)

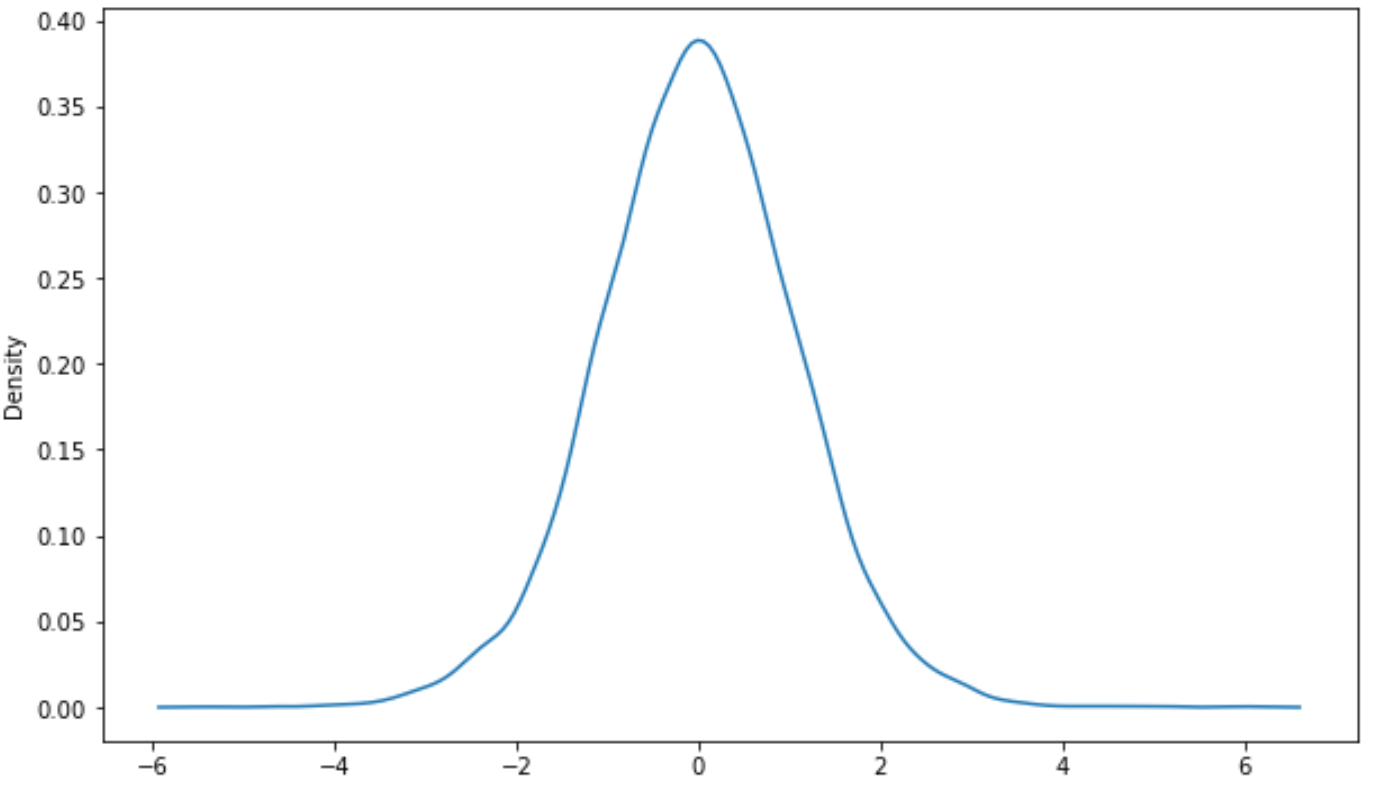
Додаткові ресурси

Наступні посібники надають додаткову інформацію про розподіл:

Нормальний розподіл проти розподілу t: у чому різниця?
Калькулятор зворотного t-розподілу