Повний посібник: як інтерпретувати результати anova в excel
Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.
У наведеному нижче прикладі наведено повний посібник щодо інтерпретації результатів одностороннього дисперсійного аналізу в Excel.
Приклад: як інтерпретувати результати ANOVA в Excel
Припустімо, що вчитель навмання просить 30 студентів у своєму класі використати один із трьох методів навчання для підготовки до іспиту.
На наступному скріншоті показано бали студентів на основі використаного ними методу:
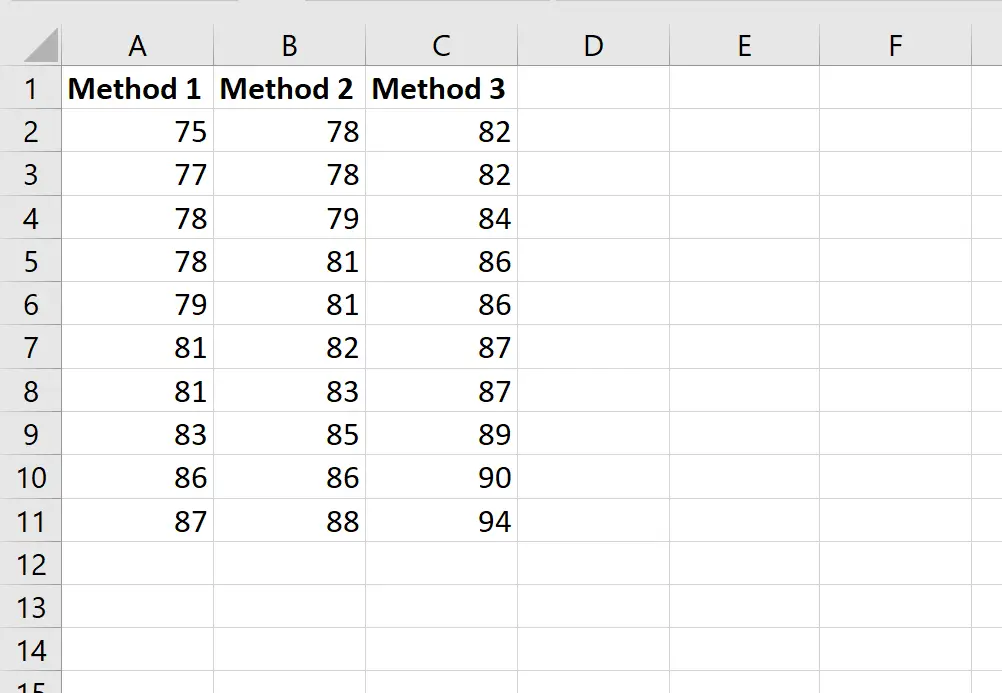
Припустімо, що вчитель хоче виконати односторонній дисперсійний аналіз, щоб визначити, чи однакові середні бали в трьох групах.
Щоб виконати односторонній дисперсійний аналіз у Excel, клацніть вкладку «Дані» на верхній стрічці, а потім клацніть «Аналіз даних» у групі «Аналіз» .

Якщо ви не бачите опцію «Аналіз даних » , спочатку потрібно завантажити безкоштовне програмне забезпечення Analysis ToolPak .
Після натискання на нього з’явиться нове вікно. Виберіть Anova: Single Factor і натисніть OK .
У новому вікні, що з’явиться, введіть таку інформацію:
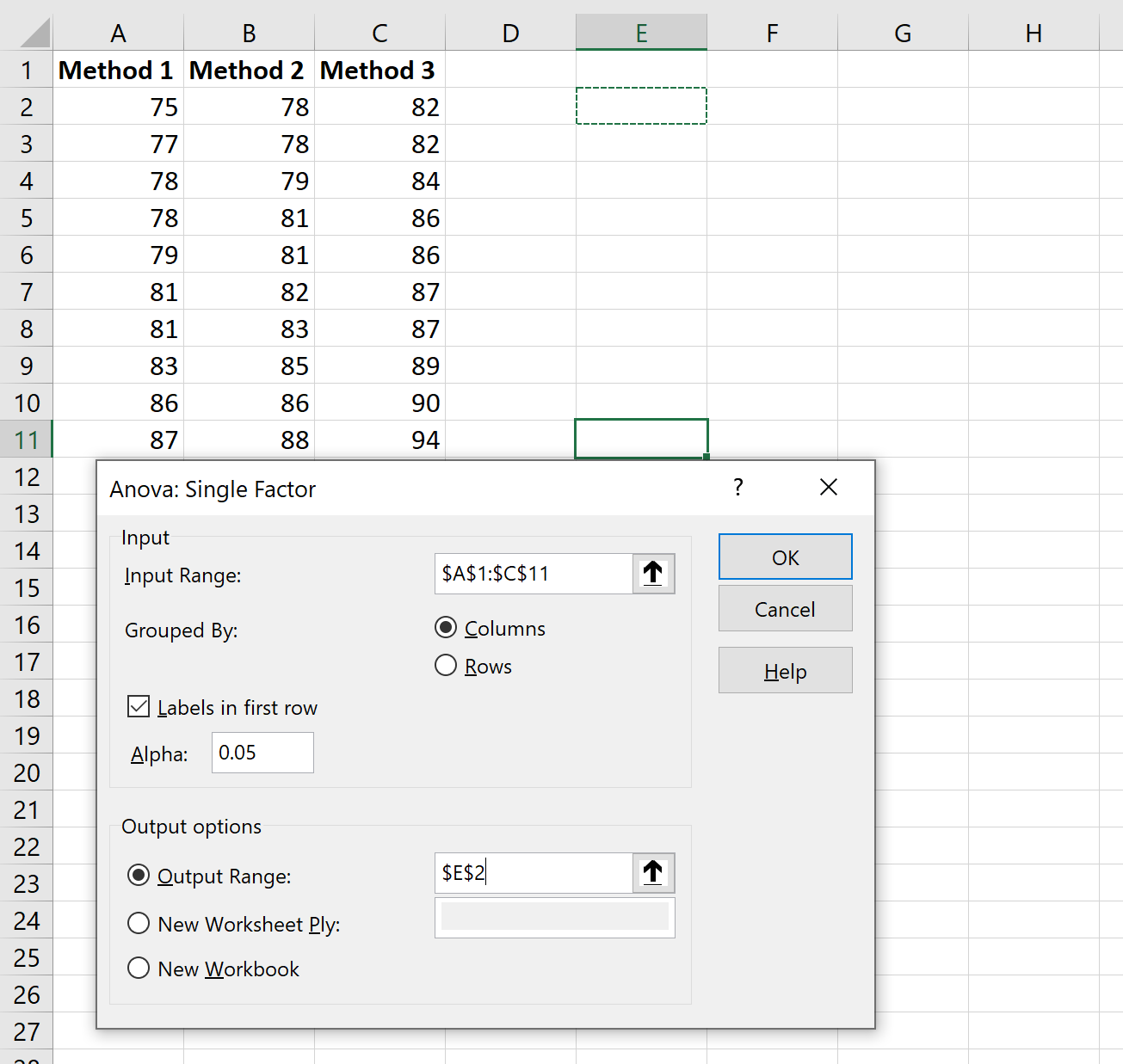
Після натискання кнопки OK з’являться результати одностороннього дисперсійного аналізу:
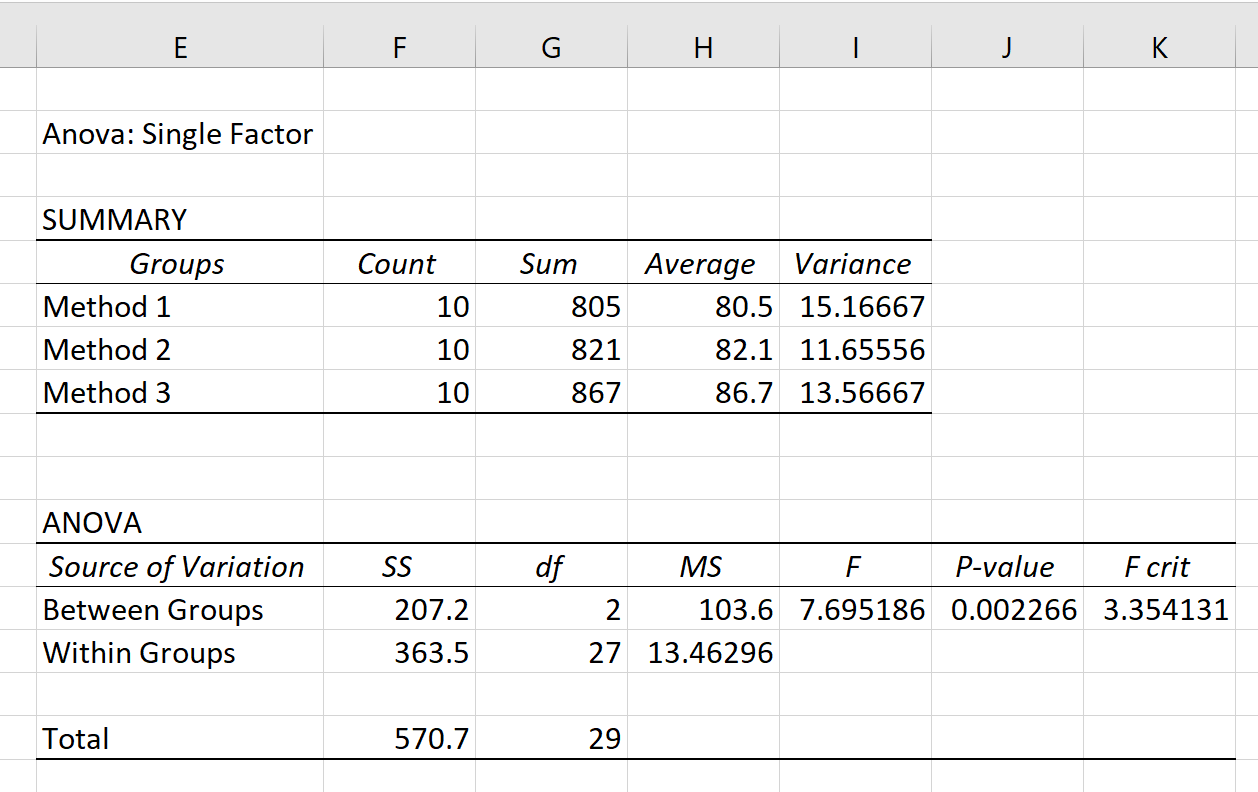
У результаті відображаються дві таблиці: SUMMARY і ANOVA .
Ось як інтерпретувати значення в кожній таблиці:
ПІДСУМНА таблиця :
- Групи : назви груп
- Підрахунок : кількість спостережень у кожній групі
- Сума : сума значень кожної групи
- Середнє : середнє значення в кожній групі
- Дисперсія : дисперсія значень у кожній групі
Ця таблиця надає нам кілька корисних підсумкових статистичних даних для кожної групи, яка використовується в ANOVA.
З цієї таблиці ми бачимо, що студенти, які використовували метод 3, мали найвищий середній бал за іспит (86,7), але вони також мали найвищу дисперсію в балах за тест. огляд (13.56667).
Щоб визначити, чи є відмінності в групових середніх статистично значущими, ми повинні звернутися до таблиці ANOVA.
Таблиця ANOVA :
- Джерело варіації : виміряна варіація (між групами або всередині груп)
- SS : сума квадратів для кожного джерела варіації
- df : Ступені свободи, обчислені як #groups-1 для df Between та #observations – #groups для df Within
- MS : середня сума квадратів, обчислена в SS/df
- F : загальне значення F, розраховане як MS між / MS в межах
- P-value : P-value, що відповідає загальному F-значенню
- F crit : критичне значення F, яке відповідає α = 0,05
Найважливішим значенням у цій таблиці є p-value , яке дорівнює 0,002266 .
Нагадаємо, що односторонній дисперсійний аналіз використовує такі нульові та альтернативні гіпотези:
- H 0 : Усі групові середні рівні.
- H A : Не всі середні показники групи однакові.
Оскільки p-значення менше α = 0,05, ми відхиляємо нульову гіпотезу одностороннього дисперсійного аналізу та робимо висновок, що у нас є достатньо доказів, щоб стверджувати, що всі групові середні не рівні.
Це означає, що не всі три методи навчання дають однакові середні оцінки за іспит.
Примітка . Ви також можете порівняти загальне значення F із критичним значенням F, щоб визначити, чи варто відхиляти нульову гіпотезу. У цьому випадку, оскільки загальне значення F більше, ніж критичне значення F, ми б відхилили нульову гіпотезу. Зауважте, що підхід із значенням p і підхід із критичним значенням F завжди призводять до однакових висновків.
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати різні дисперсійні аналізи в Excel:
Як виконати односторонній дисперсійний аналіз в Excel
Як виконати двосторонній дисперсійний аналіз у Excel
Як виконати дисперсійний аналіз повторних вимірювань у Excel
Як виконати вкладений ANOVA в Excel