Вибіркове середнє

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

З цієї статті ви дізнаєтеся, що таке вибіркове середнє в статистиці. Так само ви знайдете, як обчислити середнє значення вибірки, розв’язану вправу та, крім того, онлайн-калькулятор для обчислення середнього значення будь-якої вибірки.

Що означає вибірка?

У статистиці вибіркове середнє – це середнє значення у вибірці. Щоб обчислити середнє значення вибірки, усі значення у вибірці потрібно додати, а потім розділити на загальну кількість даних у вибірці.

Символ зразка означає

$\overline{x}$

У статистичному дослідженні, як правило, не всі значення генеральної сукупності відомі, тому вибірка генеральної сукупності відбирається для її аналізу та екстраполяції отриманих висновків на всю сукупність. Таким чином, вибіркове середнє використовується для оцінки середнього значення сукупності.

Приклад формули середнього

Вибіркове середнє дорівнює сумі всіх значень вибірки, поділеної на розмір вибірки. Тобто, щоб обчислити вибіркове середнє, усі значення у вибірці додаються, а потім діляться на загальну кількість даних у вибірці.

Тому формула для розрахунку вибіркового середнього має вигляд:

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 Ви можете скористатися калькулятором нижче, щоб обчислити вибіркове середнє значення будь-якого набору даних.

Майте на увазі, що середнє значення вибірки обчислюється з використанням даних вибірки, тому значення середнього значення сукупності може відрізнятися від обчисленого значення.

Приклад розрахунку середнього вибіркового значення

Тепер, коли ми знаємо визначення вибіркового середнього значення та його формулу, давайте подивимося, як отримати вибіркове середнє з набору даних, розв’язавши простий приклад.

Хосе хоче переїхати в центр міста, але у нього мало часу, тому він не може проаналізувати ціни на всі квартири, які здаються в оренду. Тож ви вирішили подивитися лише на вартість оренди п’яти квартир (показано нижче), щоб дізнатися, скільки вам коштуватиме проживання в центрі міста. Яка середня ціна зразка?

600 євро 430 євро 820 євро 575 євро 950 євро

Щоб знайти вибіркове середнє, нам потрібно скласти всі вибіркові значення, а потім розділити на загальну кількість спостережень, яка дорівнює 5. Отже, ми застосовуємо формулу вибіркового середнього:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

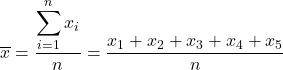
Далі підставляємо дані у формулу і обчислюємо вибіркове середнє:

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

Коротше кажучи, середня ціна вибірки квартир, відібраних для вибірки, становить 675 євро.

Приклад калькулятора середнього значення

Введіть дані будь-якої статистичної вибірки в наведений нижче калькулятор, щоб обчислити її середнє значення. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Середнє значення вибірки та середнє значення сукупності

Середнє значення сукупності – це середнє значення статистичної сукупності . Таким чином, середня популяція є середньою для всіх елементів, щодо яких планується провести статистичне дослідження.

Таким чином, різниця між середнім значенням вибірки та середнім значенням сукупності полягає в тому, що середнє значення вибірки є середнім значенням вибірки, тоді як середнє значення сукупності є середнім значенням у сукупності.

Щоб відрізнити середнє значення вибірки від середнього сукупності, їх позначають різними символами. Символ зразка означає

$\overline{x}$

, тоді як символ населення означає

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

Вибіркове середнє використовується для оцінки значення середнього генеральної сукупності, що можна зробити за допомогою точкової оцінки або інтервальної оцінки .

➤ Дивіться: Яка середня кількість населення?

Вибірковий розподіл вибіркових середніх

Нарешті, давайте подивимося, що означає вибірковий розподіл вибірки, оскільки це статистична концепція, яка може заплутати.

По-перше, давайте почнемо з визначення того, що таке розподіл вибірки. Вибірковий розподіл — це розподіл, який є результатом урахування всіх можливих вибірок із статистичної сукупності.

Таким чином, вибірковий розподіл вибіркового середнього є розподілом, який є результатом обчислення середнього значення кожної можливої вибірки із сукупності. Тобто, якщо ми вивчаємо всі можливі вибірки з сукупності та обчислюємо середнє значення кожної з вибірок, набір обчислених значень є вибірковим розподілом вибіркового середнього.

Підсумовуючи, хоча вибіркове середнє значення та вибірковий розподіл мають подібні назви, необхідно знати, як їх розрізняти: вибіркове середнє – це статистичний параметр, який обчислюється на основі вибірки, з іншого боку, вибірковий розподіл – це розподіл що є результатом вивчення всіх зразків, які можна зробити з сукупності.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше