Як виконати логістичну регресію в sas

Логістична регресія – це метод, який ми можемо використати для підгонки моделі регресії, коли змінна відповіді є двійковою.

Логістична регресія використовує метод, відомий як оцінка максимальної правдоподібності, щоб знайти рівняння такої форми:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

золото:

• X _j : j- ^та прогнозна змінна
• β _j : оцінка коефіцієнта для j ^-ї прогностичної змінної

Формула в правій частині рівняння передбачає логарифмічні шанси того, що змінна відповіді набере значення 1.

У наступному покроковому прикладі показано, як підігнати модель логістичної регресії в SAS.

Крок 1: Створіть набір даних

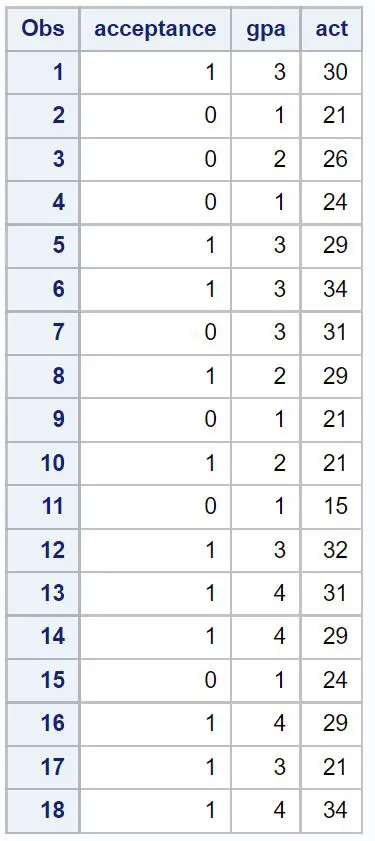
Спочатку ми створимо набір даних, що містить інформацію про наступні три змінні для 18 студентів:

• Прийняття до певного коледжу (1 = так, 0 = ні)
• GPA (шкала від 1 до 4)
• Оцінка ACT (шкала від 1 до 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Крок 2: Підгонка моделі логістичної регресії

Далі ми використаємо логістику proc , щоб відповідати моделі логістичної регресії, використовуючи «acceptance» як змінну відповіді та «gpa» і «act» як змінні предиктора.

Примітка : для SAS необхідно вказати зменшення , щоб передбачити ймовірність того, що змінна відповіді прийме значення 1. За замовчуванням SAS передбачає ймовірність того, що змінна відповіді прийме значення 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

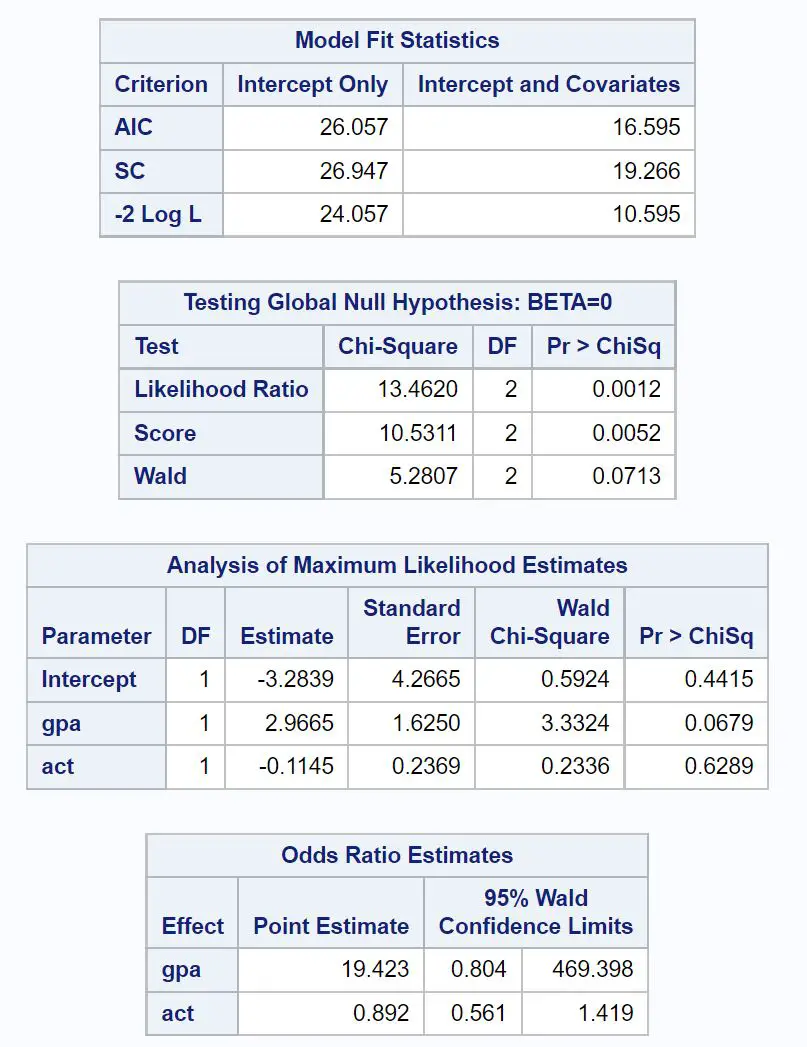
Перша цікава таблиця має назву Model Fit Statistics .

З цієї таблиці ми можемо побачити значення AIC моделі, яке виявляється 16,595 . Чим нижче значення AIC, тим краще модель відповідає даним.

Однак не існує порогу для того, що вважається «хорошим» значенням AIC . Натомість ми використовуємо AIC, щоб порівняти відповідність кількох моделей одному набору даних. Модель з найнижчим значенням AIC зазвичай вважається найкращою.

Наступна цікава таблиця має назву Перевірка глобальної нульової гіпотези: BETA=0 .

З цієї таблиці ми можемо побачити значення хі-квадрат відношення ймовірності 13,4620 із відповідним значенням p 0,0012 .

Оскільки це p-значення менше 0,05, це говорить нам про те, що модель логістичної регресії в цілому є статистично значущою.

Далі ми можемо проаналізувати оцінки коефіцієнтів у таблиці під назвою «Аналіз оцінок максимальної ймовірності» .

З цієї таблиці ми можемо побачити коефіцієнти для gpa та act, які вказують на середню зміну логарифму шансів бути прийнятим до коледжу для збільшення на одну одиницю кожної змінної.

Наприклад:

• Збільшення середнього балу на одну одиницю пов’язане зі збільшенням у середньому на 2,9665 логарифмічних шансів бути прийнятим до коледжу.
• Підвищення балу ACT на одну одиницю пов’язане зі зниженням логарифмічних шансів бути прийнятим до коледжу в середньому на 0,1145 .

Відповідні p-значення в результаті також дають нам уявлення про те, наскільки ефективна кожна змінна предиктора в прогнозуванні ймовірності бути прийнятою:

• GPA P-value: 0,0679
• P-значення ACT: 0,6289

Це говорить нам про те, що середній бал є статистично значущим показником прийняття до коледжу, тоді як оцінка ACT не є статистично значущим.

Додаткові ресурси

У наступних посібниках пояснюється, як підігнати інші моделі регресії в SAS:

Як виконати просту лінійну регресію в SAS
Як виконати множинну лінійну регресію в SAS