Критичне значення

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке критичне значення в статистиці та як його слід інтерпретувати під час перевірки гіпотез. Так само ви зможете побачити, як обчислюється критичне значення, а також кілька конкретних прикладів.

Що таке критичне значення?

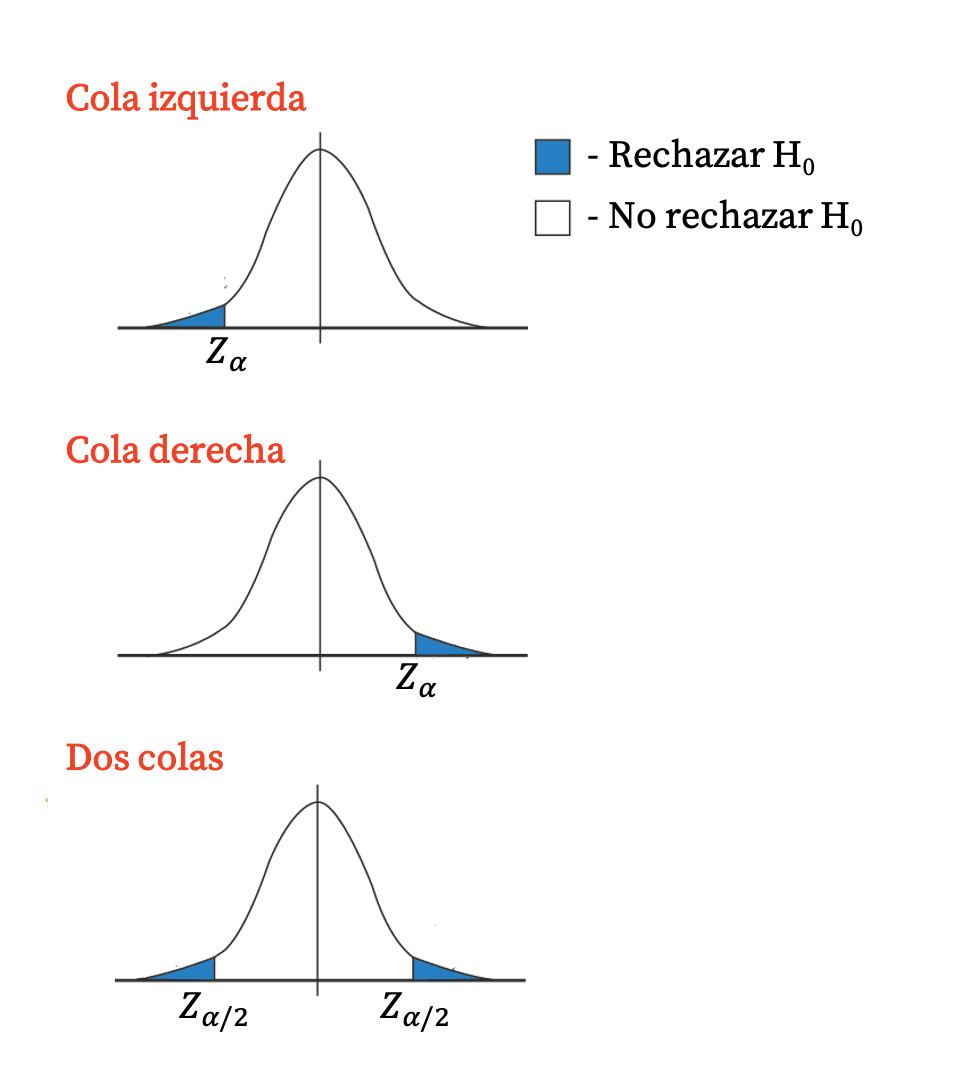
Критичне значення — це точка в розподілі тестової статистики, яка відділяє область відхилення нульової гіпотези від області її прийняття. Іншими словами, критичне значення – це значення розподілу статистичного тесту, яке позначає межу області відхилення (або критичної області).

Зазвичай критичне значення позначається символом Z _α/2 , оскільки найпоширенішим еталонним розподілом зазвичай є стандартний нормальний розподіл .

Загалом, односторонні тести мають критичне значення, оскільки область відхилення становить єдиний хвіст розподілу. З іншого боку, двосторонні тести мають два критичні значення, оскільки область відхилення відповідає обом хвостам розподілу.

У довірчих інтервалах критичні значення – це точки в еталонному розподілі, які позначають межі довірчого інтервалу.

Як розрахувати критичне значення

Потім ми побачимо, як обчислюються найпоширеніші критичні значення. Критичне значення Z і критичне значення t обчислюються для довірчого інтервалу середнього, єдина відмінність полягає в тому, що критичне значення Z обчислюється, коли стандартне відхилення генеральної сукупності відомо, а замість цього використовується критичне значення t коли відомі лише дані для одного зразка.

Критичне значення Z

Критичне значення Z використовується для визначення меж довірчого інтервалу для середнього. Точніше, він використовується, лише якщо ви знаєте стандартне відхилення сукупності.

Щоб обчислити критичне значення Z, значення, що відповідає ймовірності половини рівня значущості, має бути знайдено в стандартній таблиці нормального розподілу .

Наприклад, якщо ми хочемо визначити довірчий інтервал для середнього значення з рівнем довіри 95%, це означає, що рівень значущості становить 5%. Тому в таблиці стандартного нормального розподілу необхідно побачити, яке значення відповідає ймовірності 2,5%, оскільки довірчий інтервал для середнього є двостороннім.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Нижче ви можете побачити таблицю з найбільш використовуваними критичними значеннями Z:

Рівень достовірності (1-α)	Рівень значущості (α)	Критичне значення (Z _α/2 )
0,80	0,20	1,282
0,85	0,15	1440
0,90	0,10	1645
0,95	0,05	1960 рік
0,99	0,01	2,576
0,995	0,005	2,807
0,999	0,001	3,291

Критичне значення t

Критичне значення t використовується для визначення меж довірчого інтервалу для середнього, коли стандартне відхилення популяції невідоме.

Щоб обчислити критичне значення t, значення, яке відповідає ймовірності половини рівня значущості, має бути знайдено в таблиці t-розподілу Стьюдента , беручи до уваги, що ступені свободи t-розподілу Стьюдента є одиничними. ніж розмір вибірки.

Наприклад, якщо ми хочемо знайти довірчий інтервал із рівнем довіри 95%, а розмір вибірки становить 8, нам потрібно отримати доступ до таблиці розподілу t Стьюдента та побачити, яке значення відповідає t _0,025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Див.: Як розрахувати довірчий інтервал середнього

Критичне значення при перевірці гіпотези

Критичне значення також можна використовувати при перевірці гіпотези, щоб відхилити нульову гіпотезу (і прийняти альтернативну гіпотезу) або відхилити альтернативну гіпотезу (і прийняти нульову гіпотезу).

Якщо значення розподілу тестової статистики, що відповідає значенню p, лежить в межах інтервалу, позначеного критичними значеннями, нульова гіпотеза не відхиляється (альтернативна гіпотеза відхиляється).
Якщо значення розподілу тестової статистики, що відповідає значенню p, знаходиться за межами інтервалу, позначеного критичними значеннями, нульова гіпотеза відхиляється (альтернативна гіпотеза приймається).

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше