Як знайти медіану згрупованих даних: із прикладами
Ми часто хочемо обчислити медіану даних, згрупованих певним чином.
Пам’ятайте, що медіана представляє значення, яке лежить безпосередньо в середині набору даних, коли всі значення впорядковані від найменшого до найбільшого.
Наприклад, припустімо, що ми маємо такі згруповані дані:

Хоча неможливо обчислити точну медіану, оскільки ми не знаємовихідних значень даних , можна оцінити медіану за такою формулою:
Медіана згрупованих даних = L + W[(N/2 – C) / F]
золото:
- L : Нижня межа медіанного класу
- W : Середня ширина класу
- N : Загальна частота
- C : Кумулятивна частота до середнього класу
- F : Середня частота класу
Примітка : середній клас – це клас, який містить значення, розташоване в N/2. У наведеному вище прикладі є N = 23 загальні значення. Таким чином, середнє значення в позиції 23/2 = 11,5, що було б у класі 21-30.
У наведених нижче прикладах показано, як обчислити медіану згрупованих даних у різних сценаріях.
Приклад 1: обчислення медіани згрупованих даних
Припустімо, що ми маємо такий розподіл частот, який показує іспит, оцінений 40 студентами в певному класі:
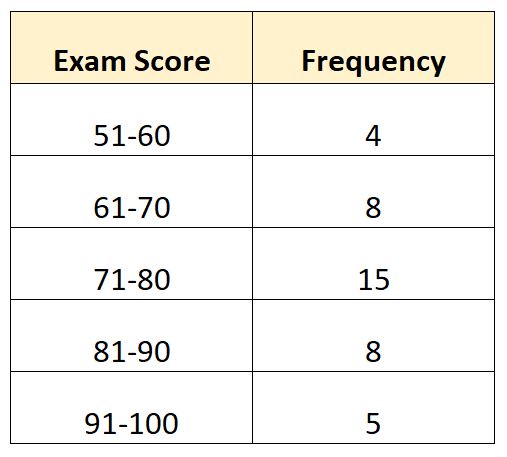
У цьому прикладі є N = 40 загальних значень. Таким чином, середнє значення знаходиться в класі, де знаходиться 40/2 = 20. 20-те за величиною значення буде в класі 71-80 .
Знаючи це, ми можемо розрахувати такі значення:
- L : Межа нижчого середнього класу: 71
- W : середня ширина класу: 9
- N : Загальна частота: 40
- C : сукупна частота до середнього класу: 12
- F : Середня частота класу: 15
Ми можемо підключити ці значення до формули для обчислення медіани розподілу:
- Медіана = L + W[(N/2 – C) / F]
- Медіана = 71 + 9[(40/2 – 12) / 15]
- Медіана = 75,8
Ми оцінюємо середній бал іспиту в 75,8 .
Приклад 2: обчислення медіани згрупованих даних
Припустимо, що ми маємо такий розподіл частот, який показує кількість очок, набраних за гру 60 баскетболістами:
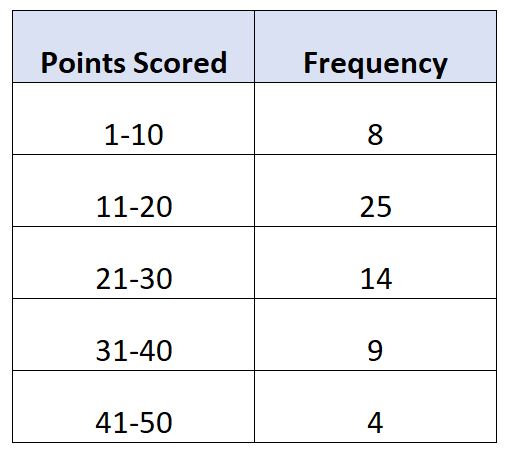
У цьому прикладі є N = 60 загальних значень. Таким чином, середнє значення знаходиться в класі, де знаходиться 60/2 = 30. 30-те найбільше значення буде в класі 11-20 .
Знаючи це, ми можемо розрахувати такі значення:
- L : Нижня межа середнього класу: 11
- W : середня ширина класу: 9
- N : Загальна частота: 60
- C : Кумулятивна частота до середнього класу: 8
- F : Середня частота класу: 25
Ми можемо підключити ці значення до формули для обчислення медіани розподілу:
- Медіана = L + W[(N/2 – C) / F]
- Медіана = 11 + 9[(60/2 – 8) / 25]
- Медіана = 18,92
Ми оцінюємо середній іспитовий бал 18,92 .
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші поширені операції із згрупованими даними:
Як знайти середнє значення та стандартне відхилення згрупованих даних
Як знайти режим згрупованих даних
Як розрахувати процентиль рейтингу для згрупованих даних