Перевірка гіпотези на різницю в середніх
У цій статті пояснюється, що таке перевірка гіпотези різниці середніх у статистиці та для чого вона використовується. Крім того, ви дізнаєтесь, як виконати перевірку гіпотези щодо різниці середніх значень і покроково розв’язану вправу.
Що таке перевірка гіпотези для середньої різниці?
Перевірка гіпотези на різницю середніх значень — це статистичний тест, який використовується для відхилення або прийняття гіпотези про те, що середні значення двох сукупностей різні. Тобто перевірка гіпотези різниці в середніх значеннях використовується для визначення того, чи є середні значення двох популяцій однаковими чи різними.
Майте на увазі, що рішення, прийняті під час перевірки гіпотези, ґрунтуються на попередньо встановленому рівні достовірності , тому не можна гарантувати, що результат перевірки гіпотези завжди буде правильним, а радше те, що це найімовірніший результат, який є істинним.
Перевірка гіпотези на різницю двох середніх включає обчислення тестової статистики та порівняння її з критичним значенням, щоб відхилити нульову гіпотезу чи ні. Нижче ми побачимо, як виконати перевірку гіпотези на різницю середніх.
Зрештою, пам’ятайте, що в статистиці перевірка гіпотез також може називатися протиставленням гіпотез, перевіркою гіпотез або перевіркою значущості.
Формула перевірки гіпотез для різниці середніх
Формула, яку слід використовувати для перевірки гіпотез про різницю в середніх значеннях, змінюється залежно від того, чи відомі дисперсії сукупності, і, якщо ні, чи можна припустити, що вони однакові чи різні. Отже, у цьому розділі ми побачимо, яку формулу використовувати залежно від випадку.
Відомі варіації
Формула для розрахунку статистики перевірки гіпотези для різниці середніх значень, коли дисперсії відомі, така:

золото:
-

це статистика перевірки гіпотези для різниці двох середніх значень з відомою дисперсією, яка відповідає стандартному нормальному розподілу.
-

це середнє значення сукупності 1.
-

це середнє значення сукупності 2.
-

є середнім значенням зразка 1.
-

є середнім значенням зразка 2.
-

є стандартним відхиленням сукупності 1.
-

є стандартним відхиленням сукупності 2.
-

розмір вибірки 1.
-

розмір вибірки 2.
Майте на увазі, що це найменш поширений випадок, тому ця формула використовується лише в окремих випадках.
Невідомі та рівні відхилення
Формула для розрахунку статистики перевірки гіпотези для різниці середніх значень, коли дисперсії генеральної сукупності невідомі, але вважаються рівними :

золото:
-

це статистика перевірки гіпотези для різниці середніх значень з невідомими дисперсіями, яка відповідає t-розподілу Стьюдента з n 1 + n 2 -2 ступенями свободи.
-

це середнє значення сукупності 1.
-

це середнє значення сукупності 2.
-

є середнім значенням зразка 1.
-

є середнім значенням зразка 2.
-

є комбінованим стандартним відхиленням.
-

розмір вибірки 1.
-

розмір вибірки 2.
Сукупне стандартне відхилення двох зразків обчислюється за такою формулою:

Невідомі та різні варіації
Коли дисперсії генеральної сукупності невідомі і, крім того, вони вважаються різними, формула для розрахунку статистики перевірки гіпотези для різниці середніх має такий вигляд:

золото:
-

це статистика перевірки гіпотези для різниці середніх значень з невідомими дисперсіями, яка відповідає t-розподілу Стьюдента.
-

це середнє значення сукупності 1.
-

це середнє значення сукупності 2.
-

є середнім значенням зразка 1.
-

є середнім значенням зразка 2.
-

є стандартним відхиленням сукупності 1.
-

є стандартним відхиленням сукупності 2.
-

розмір вибірки 1.
-

розмір вибірки 2.
Однак у цьому випадку ступені вільності t-розподілу Стьюдента розраховуються за такою формулою:

Конкретний приклад перевірки гіпотези на різницю середніх
Щоб закінчити засвоєння концепції перевірки гіпотези на основі різниці в середніх, ми розглянемо конкретний приклад цього типу перевірки гіпотези.
- Ви хочете провести статистичне дослідження заробітної плати двох конкуруючих компаній, точніше, ви хочете визначити, чи відрізняється середня заробітна плата в двох компаніях. Для цього береться вибірка з 47 працівників з однієї компанії та ще одна вибірка з 55 працівників з іншої компанії. З першої вибірки отримано середню зарплату 40 000 доларів США та стандартне відхилення 12 000 доларів США, а з другої вибірки – середню зарплату 46 000 доларів США та стандартне відхилення 18 000 доларів США. Виконайте перевірку гіпотези з рівнем значущості 5%, щоб визначити, чи відрізняються середні зарплати чи ні.
У цьому випадку нульова гіпотеза та альтернативна гіпотеза перевірки гіпотези на різницю двох середніх є такими:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
У цьому випадку розриви населення невідомі, але можна припустити, що вони рівні, оскільки це конкуруючі компанії, а умови роботи на ринку, на якому вони працюють, дуже схожі. Таким чином, формула для статистики перевірки гіпотези для різниці середніх, яку ми повинні використовувати, така:

Тому ми обчислюємо об’єднане стандартне відхилення двох вибірок:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
Тепер ми застосуємо формулу перевірки гіпотези для різниці середніх:
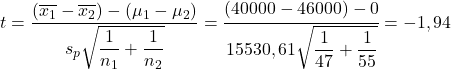
З іншого боку, ми шукаємо критичне значення перевірки гіпотези для різниці середніх у таблиці t Стьюдента :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
Тоді, оскільки абсолютне значення тестової статистики менше критичного тестового значення, нульова гіпотеза приймається, а альтернативна гіпотеза відхиляється.
![]()