Як виконати тест крускала-уолліса в sas

Критерій Крускала-Уолліса використовується для визначення того, чи існує статистично значуща різниця між медіанами трьох або більше незалежних груп.

Це вважається непараметричним еквівалентом одностороннього дисперсійного аналізу .

Цей підручник надає покроковий приклад того, як виконати тест Крускала-Уолліса в SAS.

Крок 1: Введіть дані

Припустімо, дослідники хочуть знати, чи призводять три різні добрива до різних рівнів росту рослин.

Вони випадковим чином вибирають 30 різних рослин і ділять їх на три групи по 10 рослин, вносячи в кожну групу різні добрива. Через місяць вимірюють висоту кожної рослини.

Ми введемо такі дані в SAS, які показують загальний ріст (у дюймах) кожної з 10 рослин у кожній групі:

 /*create dataset*/
data fertilizer_data;
    input fertilizer $growth;
    datalines ;
fert1 7
fert1 14
fert1 14
fert1 13
fert1 12
fert1 9
fert1 6
fert1 14
fert1 12
fert1 8
fert2 15
fert2 17
fert2 13
fert2 15
fert2 15
fert2 13
fert2 9
fert2 12
fert2 10
fert2 8
fert3 6
fert3 8
fert3 8
fert3 9
fert3 5
fert3 14
fert3 13
fert3 8
fert3 10
fert3 9
;
run ;

Крок 2: Виконайте тест Крускала-Уолліса

Далі ми використаємо оператор proc npar1way , щоб виконати тест Крускала-Уолліса, щоб порівняти середній ріст рослин між трьома групами добрив:

 /*perform Kruskal-Wallis test*/
proc npar1way data =fertilizer_data wilcoxon dscf ;
    class fertilizer;
    vargrowth ;
run ;

Крок 3: Інтерпретація результатів

У першій таблиці результатів показано загальну статистику тесту Хі-квадрат і відповідне значення p для тесту Краскела-Уолліса:

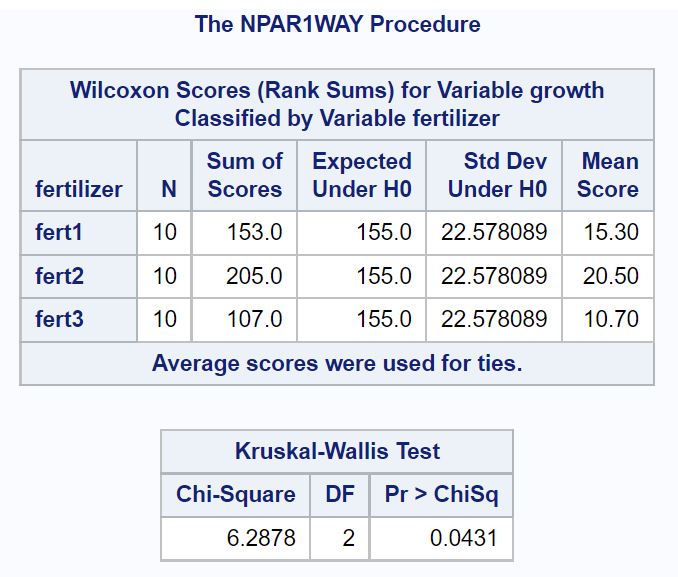
P-значення тесту становить 0,0431 . Оскільки це значення менше 0,05, ми відхиляємо нульову гіпотезу про те, що середній ріст рослин є однаковим для всіх трьох добрив.

Це означає, що ми маємо достатньо доказів, щоб зробити висновок, що тип добрива, який використовується, викликає статистично значущі відмінності у рості рослин.

Таблиця остаточних результатів показує p-значення для попарних порівнянь між кожною з трьох груп:

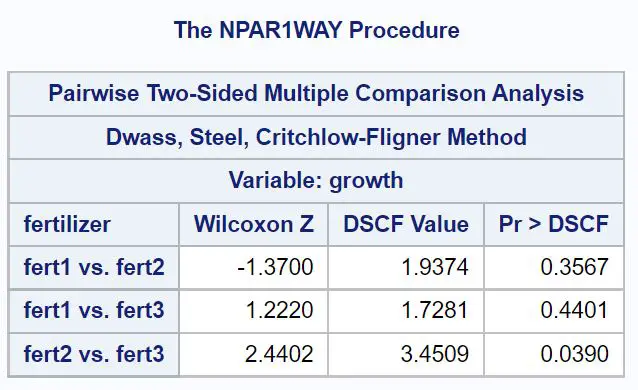
З цієї таблиці ми можемо побачити, що єдине значення p нижче 0,05 є порівнянням між добривом 2 і добривом 3, яке має значення p 0,0390 .

Це означає, що існує статистично значуща різниця у зростанні рослин між добривом 2 і добривом 3, але не між іншими парними порівняннями.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші поширені статистичні тести в SAS:

Як виконати одновибірковий t-тест у SAS
Як виконати двовибірковий t-тест у SAS
Як виконати односторонній дисперсійний аналіз у SAS
Як виконати двосторонній дисперсійний аналіз у SAS