Розподіл хі-квадрат у r: dchisq, pchisq, qchisq, rchisq
У цьому посібнику пояснюється, як використовувати розподіл хі-квадрат у R за допомогою таких функцій:
- dchisq : повертає значення функції щільності ймовірності хі-квадрат.
- pchisq : повертає значення функції щільності хі-квадрат.
- qchisq : повертає значення функції квантиля хі-квадрат.
- rchisq : генерує вектор розподілених випадкових змінних хі-квадрат.
Наступні приклади показують, як використовувати кожну з цих функцій на практиці.
dchisq
Ми часто використовуємо функцію dchisq() із функцією Curve() , щоб побудувати графік розподілу хі-квадрат із певною кількістю ступенів свободи.
Наприклад, ми можемо використати такий код, щоб побудувати графік розподілу хі-квадрат із 5 ступенями свободи:
#plot Chi_Square distribution with 5 degrees of freedom curve(dchisq(x, df= 5 ), from= 0 , to= 20 )
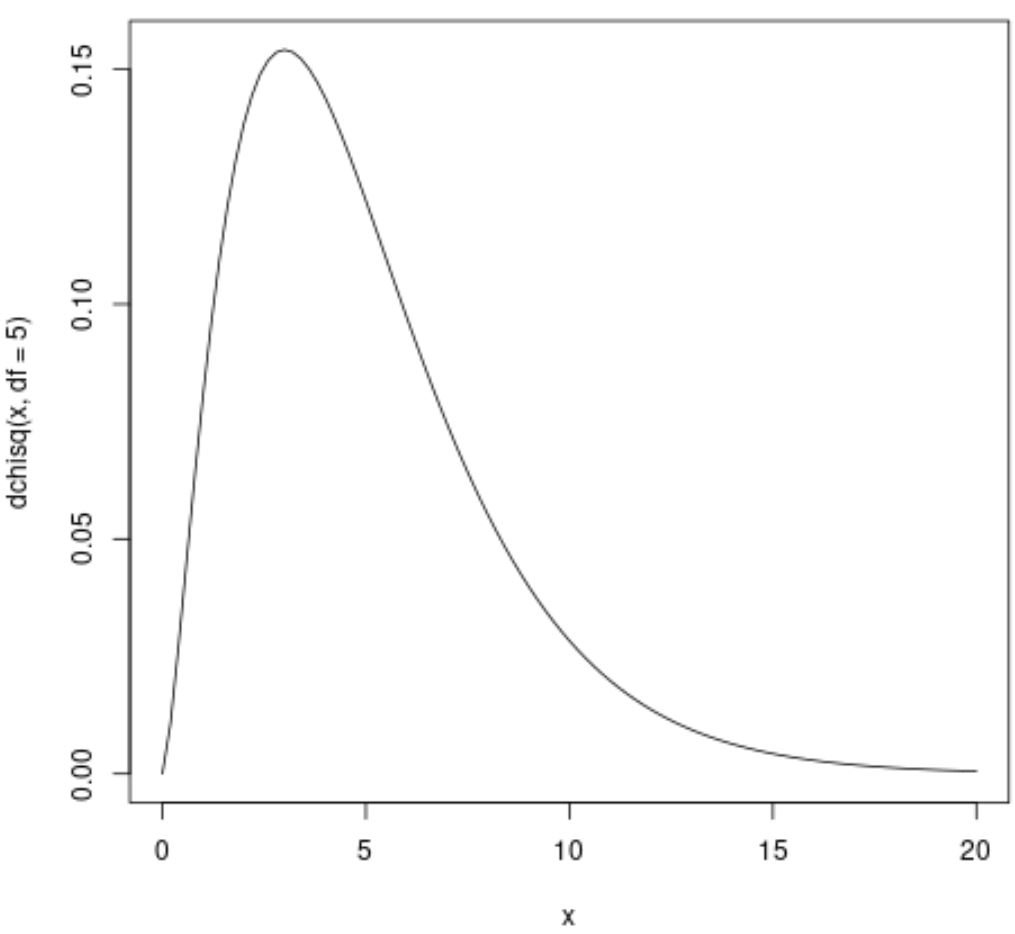
На осі абсцис відображаються значення тестової статистики хі-квадрат, а на осі у – відповідне значення функції щільності ймовірності.
Пов’язане: Як легко побудувати розподіл хі-квадрат у R
pchisq
Ми часто використовуємо pchisq() щоб знайти значення p , яке відповідає певній статистиці хі-квадрат.
Наприклад, припустімо, що ми виконуємо тест хі-квадрат незалежності та отримуємо тестову статистику X2 = 0,86404 з 2 ступенями свободи.
Ми можемо використати функцію pchisq() , щоб знайти значення p, яке відповідає цій тестовій статистиці:
#calculate p-value for given test statistic with 2 degrees of freedom 1-pchisq(0.86404, df= 2 ) [1] 0.6491964
P-значення виявляється рівним 0,6491964 .
Ми також можемо підтвердити, що це правильно, використовуючи калькулятор співвідношення хі-квадрат до значення P.
щось
Ми часто використовуємо qchisq() функція для знаходження критичного значення хі-квадрат, яке відповідає даному рівню значущості та ступеням свободи.
Наприклад, ми можемо використати наступний код, щоб знайти критичне значення Хі-квадрат, яке відповідає рівню значущості 0,05 із 13 ступенями свободи:
qchisq(p= .95 , df= 13 )
[1] 22.36203
Критичне значення виявляється 22,36203 .
Ми також можемо підтвердити, що це правильно, використовуючи калькулятор критичного значення хі-квадрат .
rchisq
Ми часто використовуємо rchisq() функція для створення списку з n випадкових значень, які відповідають розподілу хі-квадрат із заданим ступенем свободи.
Наприклад, ми можемо використати наступний код для створення списку з 1000 випадкових значень, які відповідають розподілу хі-квадрат із 5 ступенями свободи:
#make this example reproducible
set. seed ( 0 )
#generate 1000 random values that follow Chi-Square dist with df=5
values <- rchisq(n= 1000 , df= 5 )
#view first five values
head(values)
[1] 8.369701 3.130487 1.985623 5.258747 10.578594 6.360859
Ми також можемо використати функцію hist( ) для створення гістограми, щоб візуалізувати цей розподіл значень:
#create histogram to visualize distribution of values
hist(values)
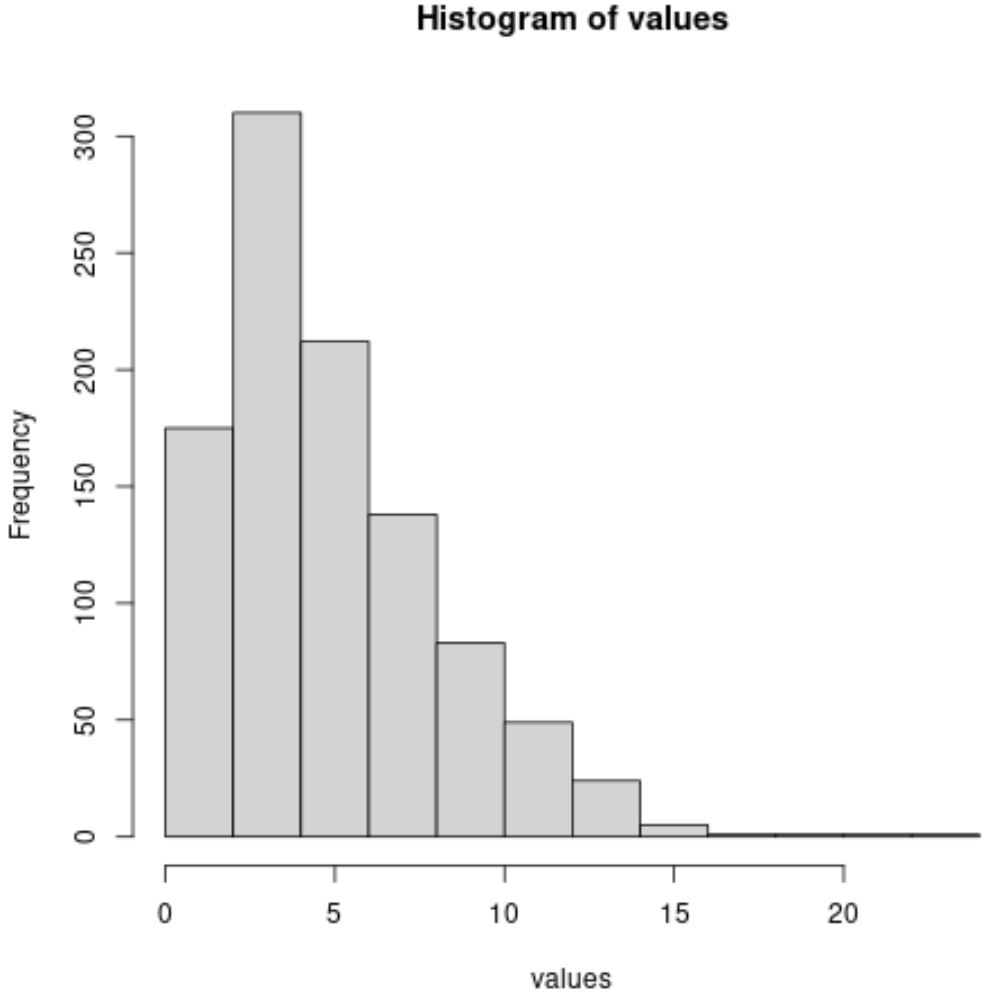
На осі абсцис відображаються значення даних, а на осі у – частота цих значень.
Додаткові ресурси
У наступних посібниках пояснюється, як працювати з іншими дистрибутивами в R:
Нормальний розподіл в R: dnorm, pnorm, qnorm і rnorm
Біноміальний розподіл в R: dbinom, pbinom, qbinom і rbinom
Розподіл риби в R: dpois, ppois, qpois і rpois