Як інтерпретувати асиметрію в статистиці: із прикладами

У статистиці ми використовуємо асиметрію для опису симетрії розподілу.

Ми говоримо, що розподіл значень даних спотворений , якщо він має «хвіст» зліва від розподілу:

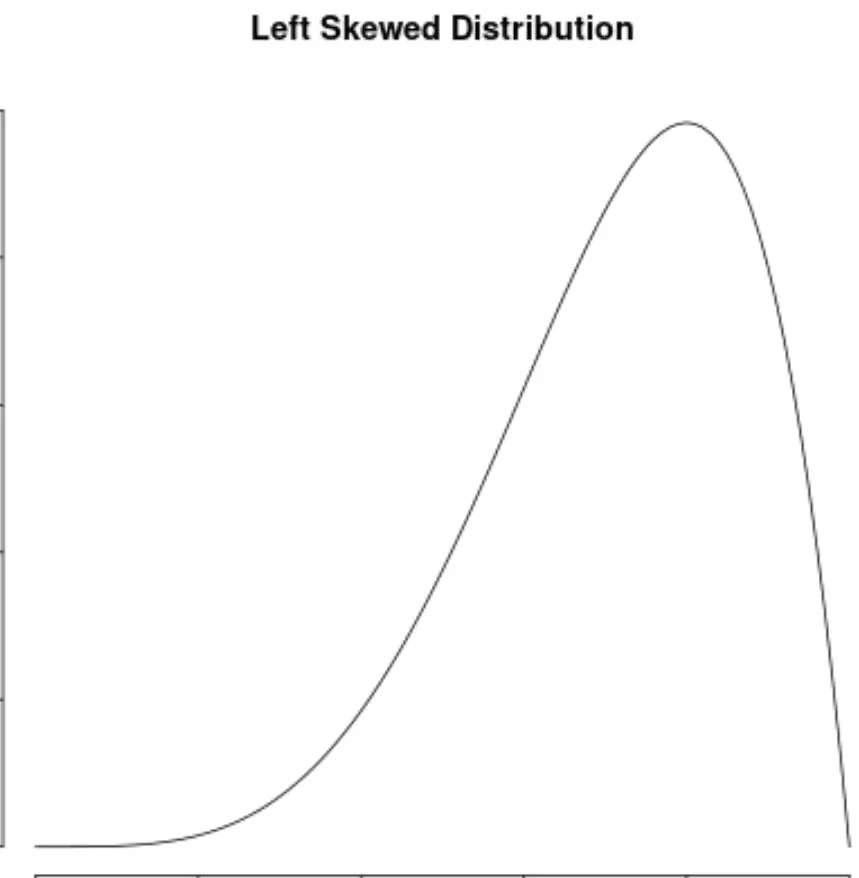
Розподіл називається скошеним вправо , якщо він має «хвіст» у правій частині розподілу:

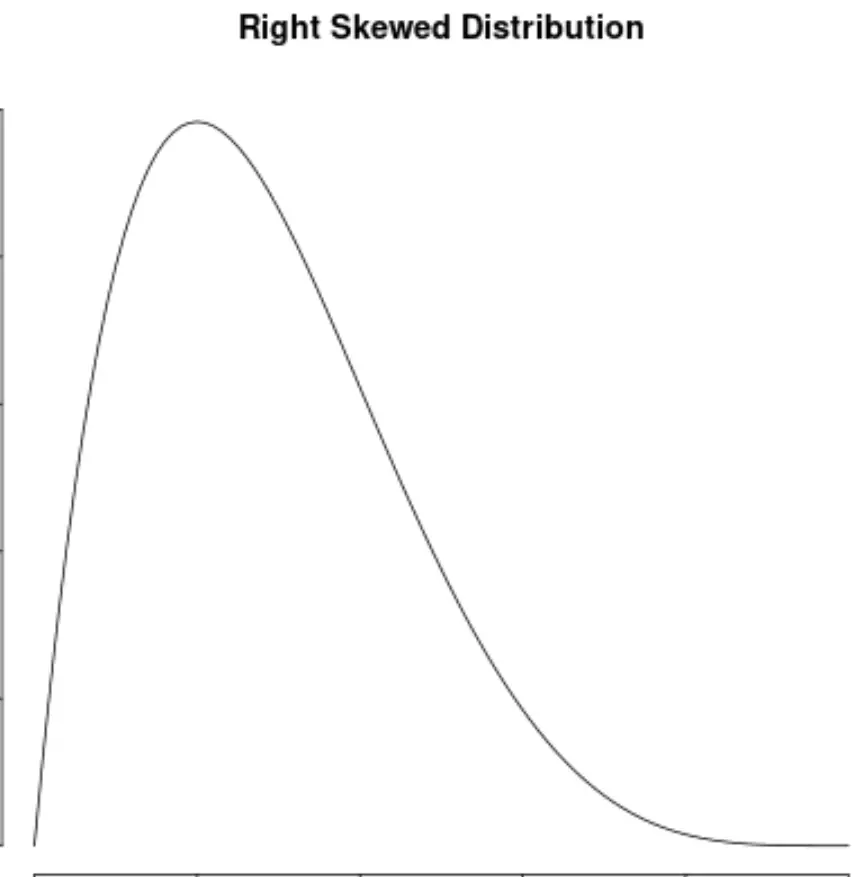
І ми говоримо, що розподіл не має асиметрії , якщо він симетричний з обох сторін:

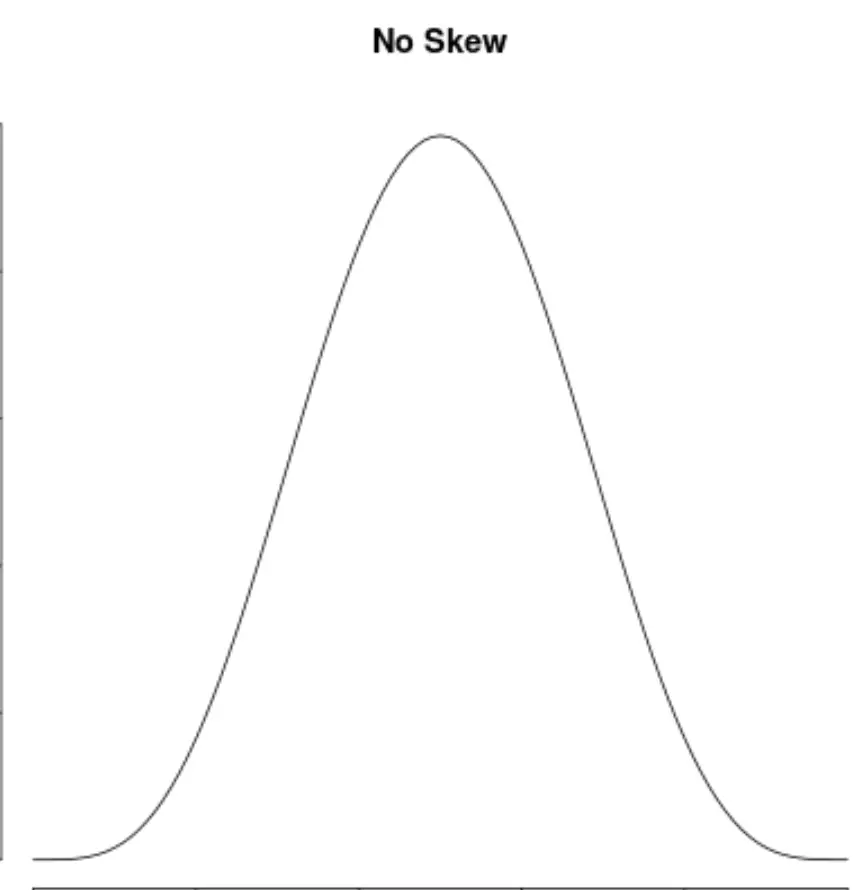
Як інтерпретувати асиметрію

Значення асиметрії може коливатися від негативної нескінченності до позитивної нескінченності.

Ось як інтерпретувати значення асиметрії:

• Від’ємне значення асиметрії вказує на те, що хвіст знаходиться ліворуч від розподілу, який розширюється до більш від’ємних значень.
• Позитивне значення асиметрії вказує на те, що хвіст знаходиться на правій стороні розподілу, який розширюється до більш позитивних значень.
• Значення нуль вказує на те, що в розподілі немає асиметрії, що означає, що розподіл є абсолютно симетричним.

Наступні приклади показують, як інтерпретувати значення асиметрії на практиці.

Приклад 1: лівосторонній розподіл

Віковий розподіл смертей у більшості груп населення зміщений вліво. Більшість людей живуть від 70 до 80 років, і все менше людей доживають до цього віку.

Якби ми створили графік щільності для візуалізації розподілу значень для віку смерті, він міг би виглядати так:

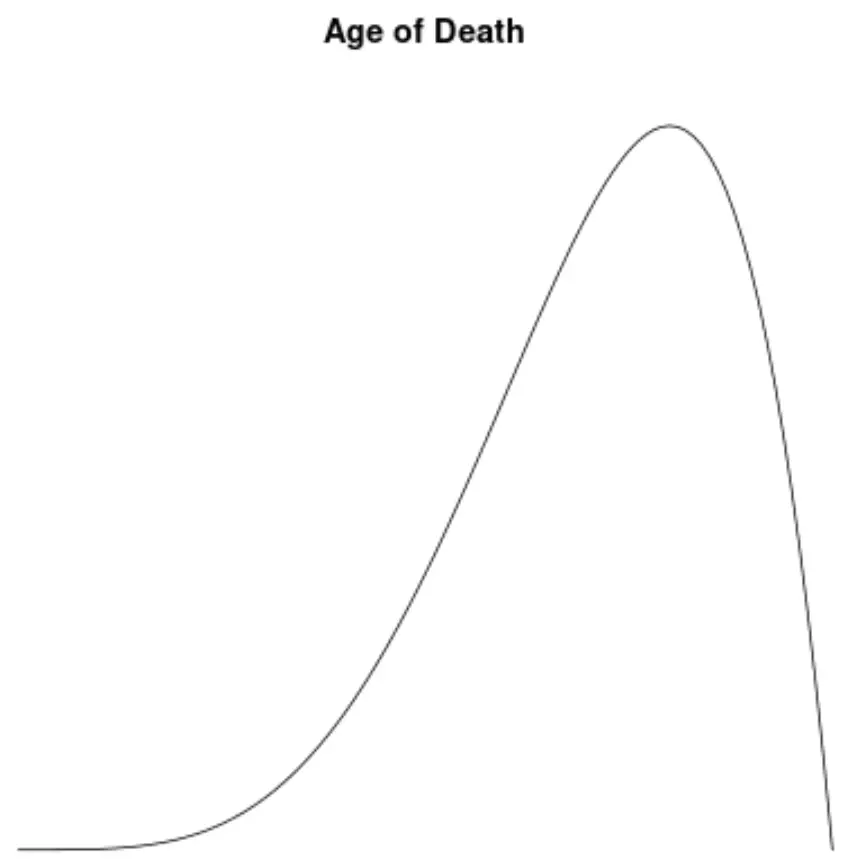
Припустімо, ми обчислюємо асиметрію цього розподілу і знаходимо, що вона дорівнює -1,3225 .

Оскільки це значення від’ємне, ми інтерпретуємо це як те, що розподіл має перекіс вліво, тобто хвіст простягається до лівої сторони розподілу.

Приклад 2: правосторонній розподіл

Розподіл доходів домогосподарств у Сполучених Штатах спотворений праворуч: більшість домогосподарств заробляє від 30 000 до 70 000 доларів на рік, але довгий правий хвіст домогосподарств заробляє набагато більше.

Якщо ми створимо графік щільності для візуалізації розподілу значень доходу домогосподарства, це може виглядати так:

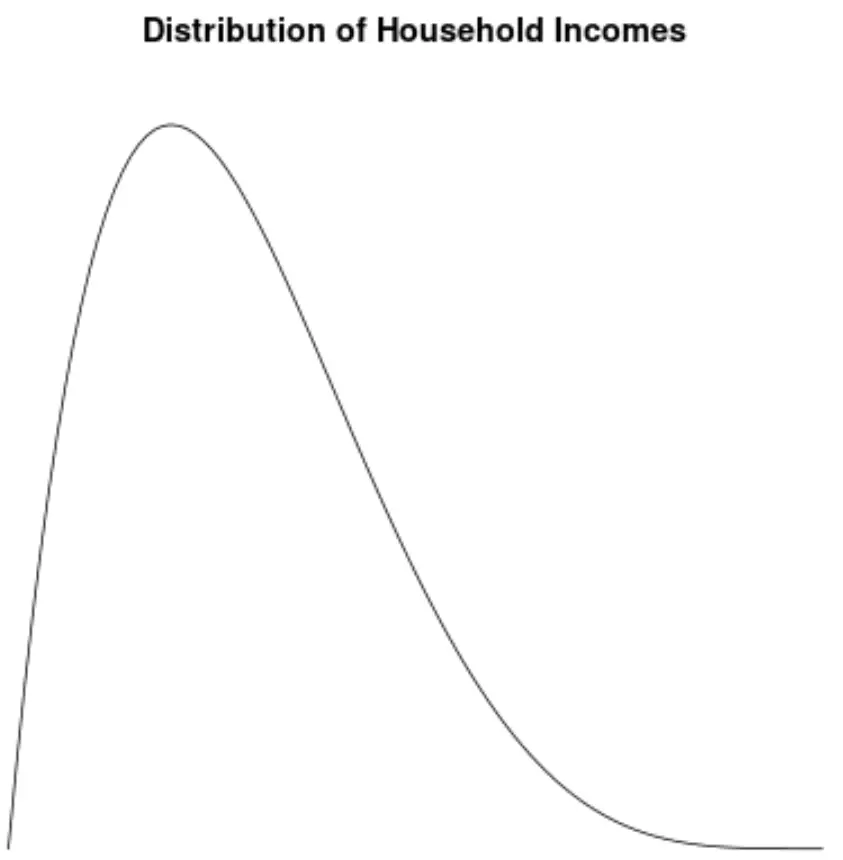
Припустимо, ми обчислюємо асиметрію цього розподілу і знаходимо, що вона дорівнює 2,0043 .

Оскільки це значення додатне, ми інтерпретуємо це як те, що розподіл має правий перекіс, тобто хвіст простягається до правого боку розподілу.

Приклад 3: відсутність упередженості

Розмір самців розподілений приблизно нормально і не має асиметрії. Наприклад, середній зріст чоловіка в Сполучених Штатах становить приблизно 69,1 дюйма. Розподіл зросту приблизно симетричний: одні нижчі, інші вищі.

Якби ми створили діаграму щільності для візуалізації розподілу зросту чоловіків у Сполучених Штатах, вона могла б виглядати так:

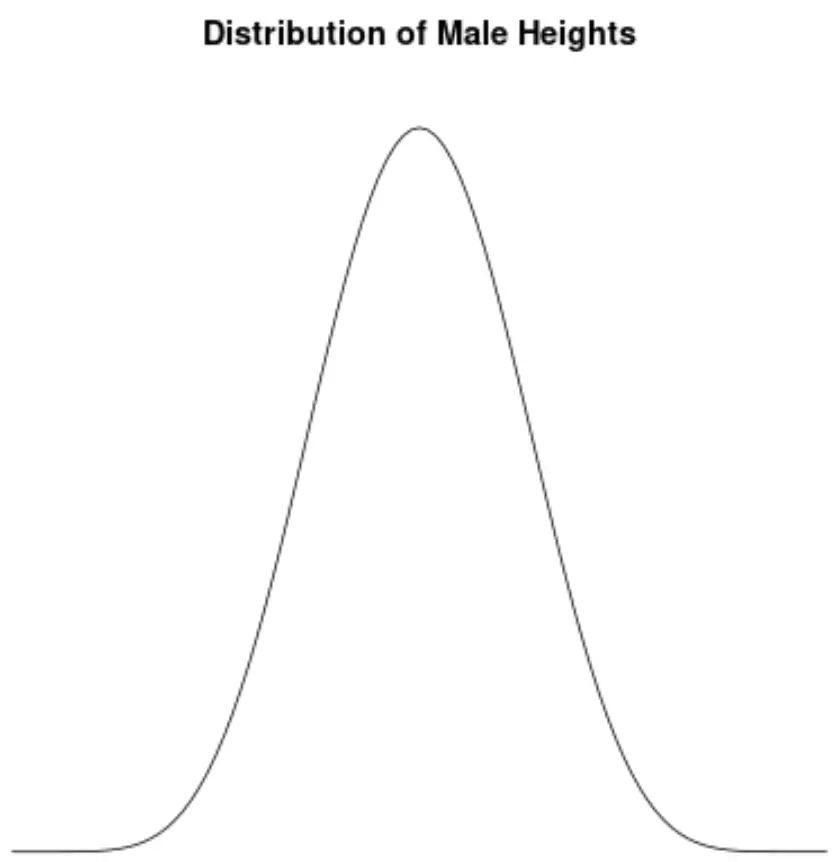
Припустимо, ми обчислюємо асиметрію цього розподілу і знаходимо, що вона становить 0,0013 .

Оскільки це значення близьке до нуля, ми інтерпретуємо це як те, що розподіл практично не має перекосів, тобто хвости з обох боків розподілу приблизно рівні.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про статистику перекосу:

5 прикладів позитивно викривлених розподілів
5 прикладів негативно викривлених розподілів
Як обчислити асиметрію в Excel
Як визначити асиметрію на прямокутних графіках