Логарифмічна регресія

У цій статті пояснюється, що таке логарифмічна регресія та як вона виконується. Крім того, ви можете побачити приклад логарифмічної регресії, щоб повністю зрозуміти концепцію.

Що таке логарифмічна регресія?

Логарифмічна регресія — це регресійна модель, яка включає в своє рівняння логарифм. Зокрема, у логарифмічній регресії береться логарифм незалежної змінної. Отже, рівняння для моделі логарифмічної регресії має вигляд y=a+b·ln(x).

Логарифмічна регресія дуже корисна для підгонки регресійної моделі, коли вибіркові дані утворюють логарифмічну криву, щоб регресійна модель краще відповідала вибірковим даним. Нижче ми побачимо, коли слід виконувати логарифмічну регресію.

Таким чином, логарифмічна регресія є різновидом нелінійної регресії, так само як експоненціальна регресія та поліноміальна регресія.

Формула логарифмічної регресії

Модель логарифмічної регресії передбачає логарифмування незалежної змінної. Отже, формула для рівняння логарифмічної регресії має вигляд y=a+b·ln(x).

золото:

• 

  є залежною змінною.

• 

  є незалежною змінною.

• 

  є коефіцієнтами регресії.

Зверніть увагу, що y=a+b·ln(x) насправді є рівнянням прямої, але замість посилання на вихідні змінні x і y, воно посилається на змінні ln(x) і y.

Коли робити логарифмічну регресію?

Нам потрібно виконати логарифмічну регресію, коли графік вибіркових даних є логарифмічною кривою, тобто коли графік точок подібний до графіка логарифмічної функції.

Подивіться на діаграму розсіювання нижче, модель лінійної регресії була підігнана до набору даних. Як бачите, лінія є непоганим наближенням даних, однак, якщо ви будете обережні, значення на початку графіка зростають швидше, ніж у кінці, тому лінія не повністю відповідає спостереженням .

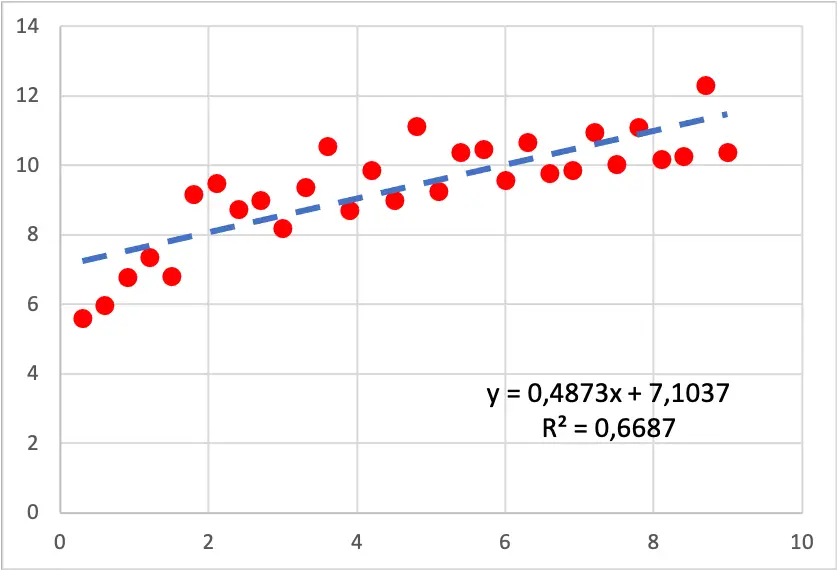
Тож варто спробувати створити модель логарифмічної регресії, оскільки виглядає так, ніби дані слідують логарифмічній кривій. Результат, отриманий за допомогою моделі логарифмічної регресії, такий:

Як ви бачите на попередньому графіку, отримана модель логарифмічної регресії краще відповідає вибірковим даним. Насправді коефіцієнт детермінації збільшився з 66,87% до 80,05%, тому тепер модель може краще пояснити вибірку даних. Тому в цьому випадку краще використовувати логістичну регресію, щоб знайти рівняння, яке наближено відповідає значенню даних.

Інші види нелінійної регресії

Три найпоширеніші випадки нелінійної регресії:

• Логарифмічна регресія : береться логарифм незалежної змінної.
• Експоненціальна регресія : незалежна змінна є експонентою рівняння.
• Поліноміальна регресія : рівняння моделі регресії має форму полінома.