Поліноміальна регресія

за Редакція 2 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке поліноміальна регресія в статистиці та як вона виконується. Крім того, ви зможете побачити приклад, у якому виконується поліноміальна регресія.

Що таке поліноміальна регресія?

Поліноміальна регресія або поліноміальна регресія — це регресійна модель, у якій зв’язок між незалежною змінною X і залежною змінною Y моделюється за допомогою полінома.

Наприклад, рівняння для моделі квадратичної поліноміальної регресії має вигляд y=β ₀ +β ₁ x+β ₂ x ² +ε.

Поліноміальна регресія корисна для підгонки наборів даних, графіки яких є поліноміальними кривими. Отже, якщо точковий графік вибірки даних має форму параболи, буде краще побудувати модель квадратичної регресії, а не модель лінійної регресії. Таким чином, рівняння регресійної моделі краще відповідатиме вибірці даних.

Зауважте, що поліноміальна регресія є типом нелінійної регресії, так само як експоненціальна регресія та логарифмічна регресія.

Формула поліноміальної регресії

Рівняння для моделі поліноміальної регресії має вигляд y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

золото:

$y$

є залежною змінною.
$x$

є незалежною змінною.
$\beta_0$

є константою рівняння поліноміальної регресії.
$\beta_i$

це коефіцієнт регресії, пов’язаний зі змінною

$x^i$

.
$\bm{\varepsilon}$

Це помилка або залишок, тобто різниця між спостережуваним значенням і значенням, оціненим за допомогою моделі.

Отже, якщо у нас є вибірка із загальною кількістю

$n$

спостережень, ми можемо запропонувати модель поліноміальної регресії у матричній формі:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

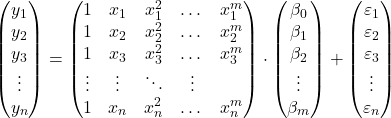
Наведений вище матричний вираз можна переписати, присвоївши літеру кожній матриці:

$Y=X\beta+\varepsilon$

Таким чином, застосовуючи критерій найменших квадратів , ми можемо отримати формулу для оцінки коефіцієнтів моделі поліноміальної регресії :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Однак виконання цих обчислень вручну є дуже трудомістким і трудомістким, тому зручніше використовувати комп’ютерне програмне забезпечення (наприклад, Minitab або Excel), яке дозволяє виконувати модель поліноміальної регресії набагато швидше.

Приклад моделі поліноміальної регресії

Тепер, коли ми знаємо визначення поліноміальної регресії та те, як вона виконується, давайте розглянемо приклад із реального життя, щоб повністю зрозуміти цю концепцію.

Перш за все, слід мати на увазі, що модель поліноміальної регресії слід виконувати, коли графік даних має форму поліноміальної кривої. Наприклад, якщо точковий графік має форму кубічної кривої, нам потрібно побудувати модель поліноміальної регресії третього ступеня.

Отже, як ви бачите на наступному зображенні, точковий графік наших даних має квадратичну форму, оскільки, коли ми збільшуємо значення незалежної змінної, залежна змінна зростає швидше. У цьому випадку була виконана модель лінійної регресії, і, як ви бачите, вона погано підходить до точок, оскільки має ділянки, у яких лінія розташована нижче всіх точок, і ділянки, у яких лінія розташована над ними.

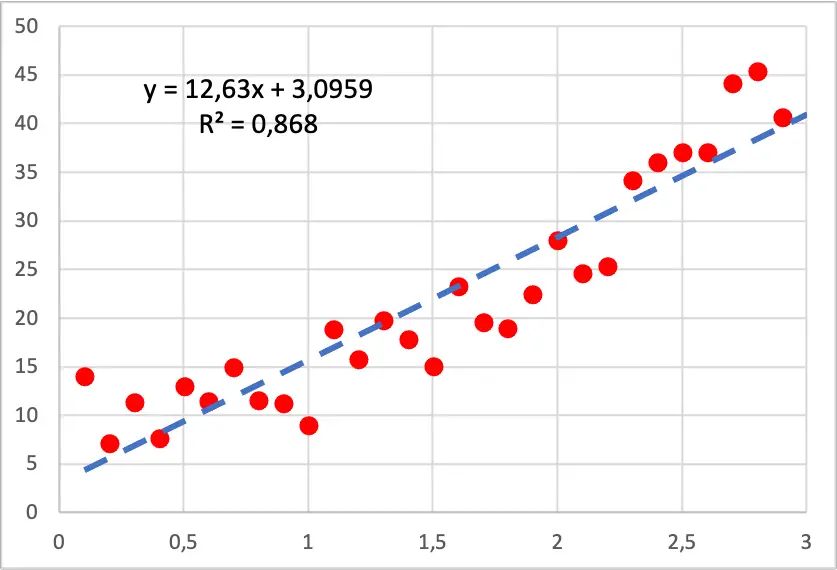
З іншого боку, якщо ми запустимо модель квадратичної поліноміальної регресії, вона набагато краще відповідає вибірці даних, як ви можете бачити на зображенні нижче.

Крім того, при розробці моделі поліноміальної регресії коефіцієнт детермінації значно покращується, оскільки він змінюється з 86,80% до 94,05%. Тому нова регресійна модель набагато краще пояснює набір даних.

З іншого боку, ще одним свідченням того, що нам потрібно виконати поліноміальну регресію, є побудова графіка залишків. Якщо в лінійній регресії графік залишків має форму параболи або полінома іншого типу, модель поліноміальної регресії, безумовно, краще відповідає досліджуваним даним.

Інші види нелінійної регресії

В основному існує три типи нелінійної регресії:

Поліноміальна регресія – рівняння моделі регресії має форму полінома.
Логарифмічна регресія : береться логарифм незалежної змінної.
Експоненціальна регресія : незалежна змінна знаходиться в показнику степеня рівняння.

➤ Див.: Логарифмічна регресія
➤ Див.: Експоненціальна регресія

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше