Як використовувати функцію logest в excel (з прикладом)

Ви можете використовувати функцію LOGEST в Excel, щоб обчислити формулу для експоненціальної кривої, яка відповідає вашим даним.

Рівняння кривої прийме такий вигляд:

y = b* ^mx

Ця функція використовує такий базовий синтаксис:

 = LOGEST ( known_y's, [known_x's], [const], [stats] )

золото:

• відомі_y : масив відомих значень y
• відомі_x : масив відомих значень x
• const : необов’язковий аргумент. Якщо TRUE, константа b обробляється нормально. Якщо значення FALSE, константа b має значення 1.
• stats : необов’язковий аргумент. Якщо TRUE, повертається додаткова статистика регресії. Якщо FALSE, додаткова регресійна статистика не повертається.

Наступний покроковий приклад показує, як використовувати цю функцію на практиці.

Крок 1: Введіть дані

Спочатку давайте введемо такий набір даних в Excel:

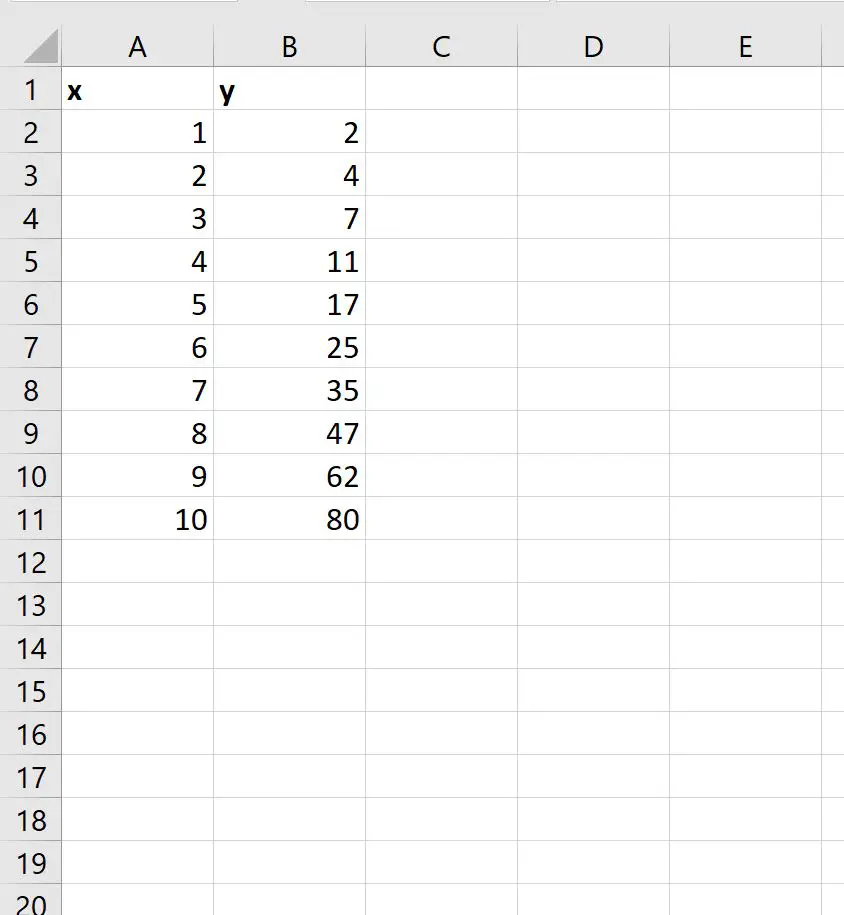
Крок 2: Візуалізуйте дані

Далі створимо швидку діаграму розсіювання x проти y, щоб переконатися, що дані справді відповідають експоненціальній кривій:

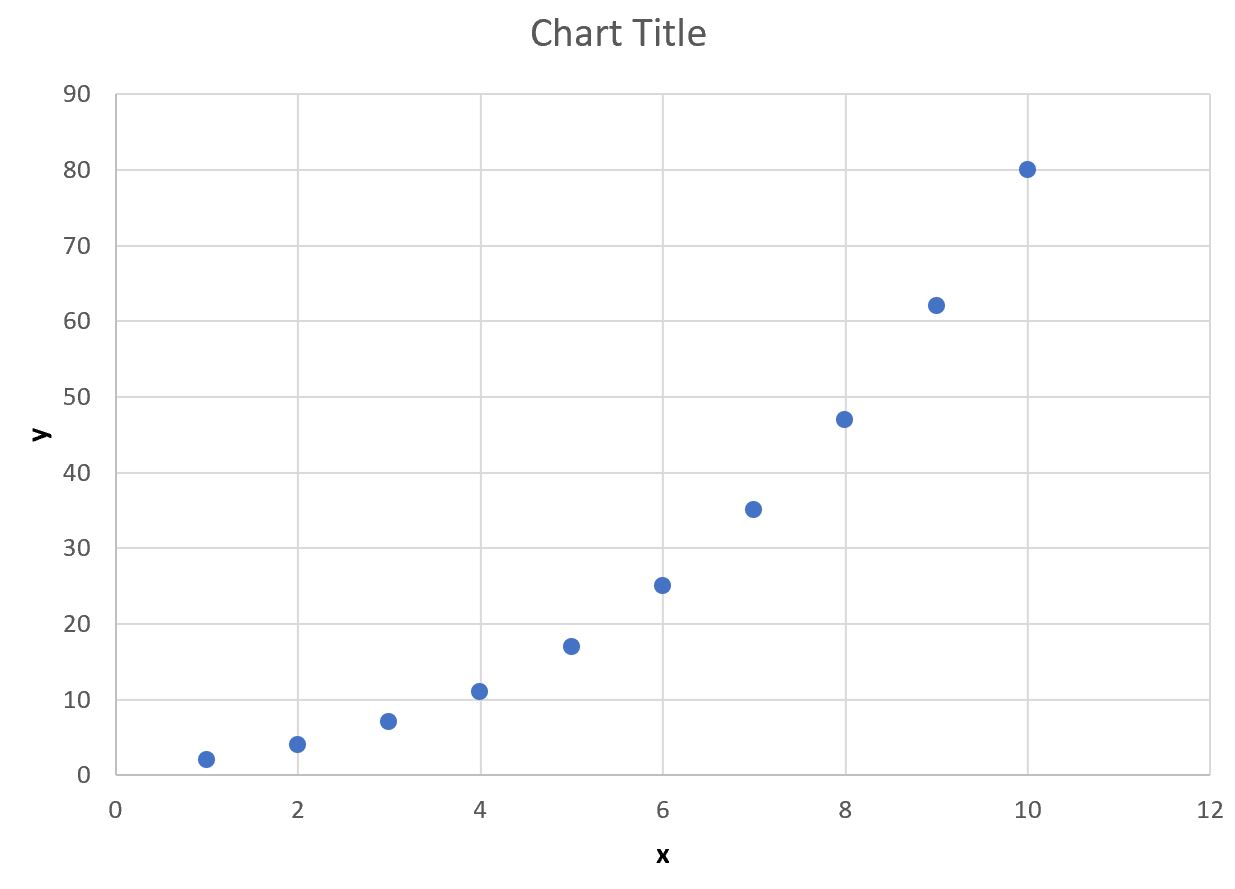
Ми бачимо, що дані справді мають експоненціальну криву.

Крок 3. Використовуйте LOGEST, щоб знайти формулу для експоненціальної кривої

Тоді ми можемо ввести таку формулу в будь-яку клітинку, щоб обчислити формулу експоненціальної кривої:

 =LOGEST( B2:B11 , A2:A11 )

На наступному знімку екрана показано, як використовувати цю формулу на практиці:

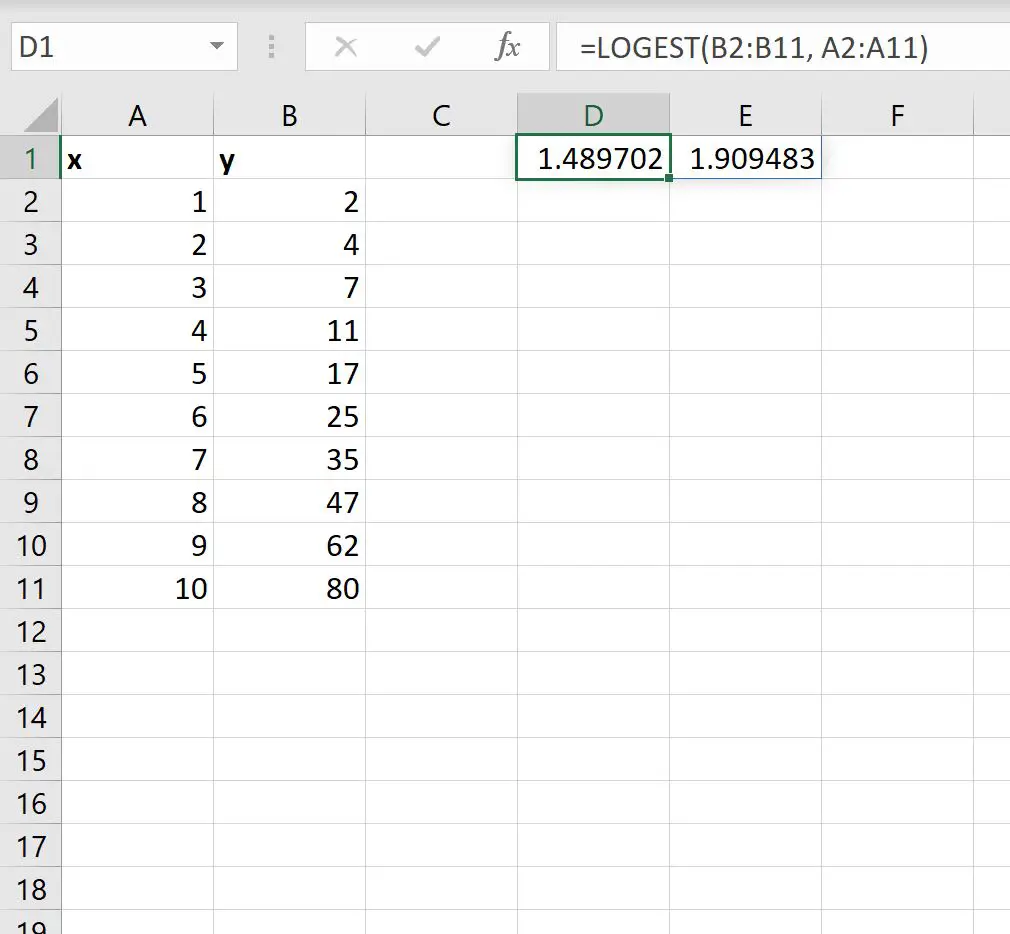
Перше значення виходу представляє значення m , а друге значення виходу представляє значення b у рівнянні:

y = b* ^mx

Отже, ми запишемо цю формулу експоненціальної кривої так:

y = 1,909483 * ^1,489702x

Потім ми могли б використати цю формулу, щоб передбачити значення y на основі значення x.

Наприклад, якщо xa має значення 8, ми передбачаємо, що y має значення 46,31 :

y = 1,909483 * 1,489702 ⁸ = 46,31

Крок 4 (необов’язково): перегляд додаткової статистики регресії

Ми можемо встановити значення аргументу stats у функції LOGEST рівним TRUE , щоб відобразити додаткову статистику регресії для підігнаного рівняння регресії:

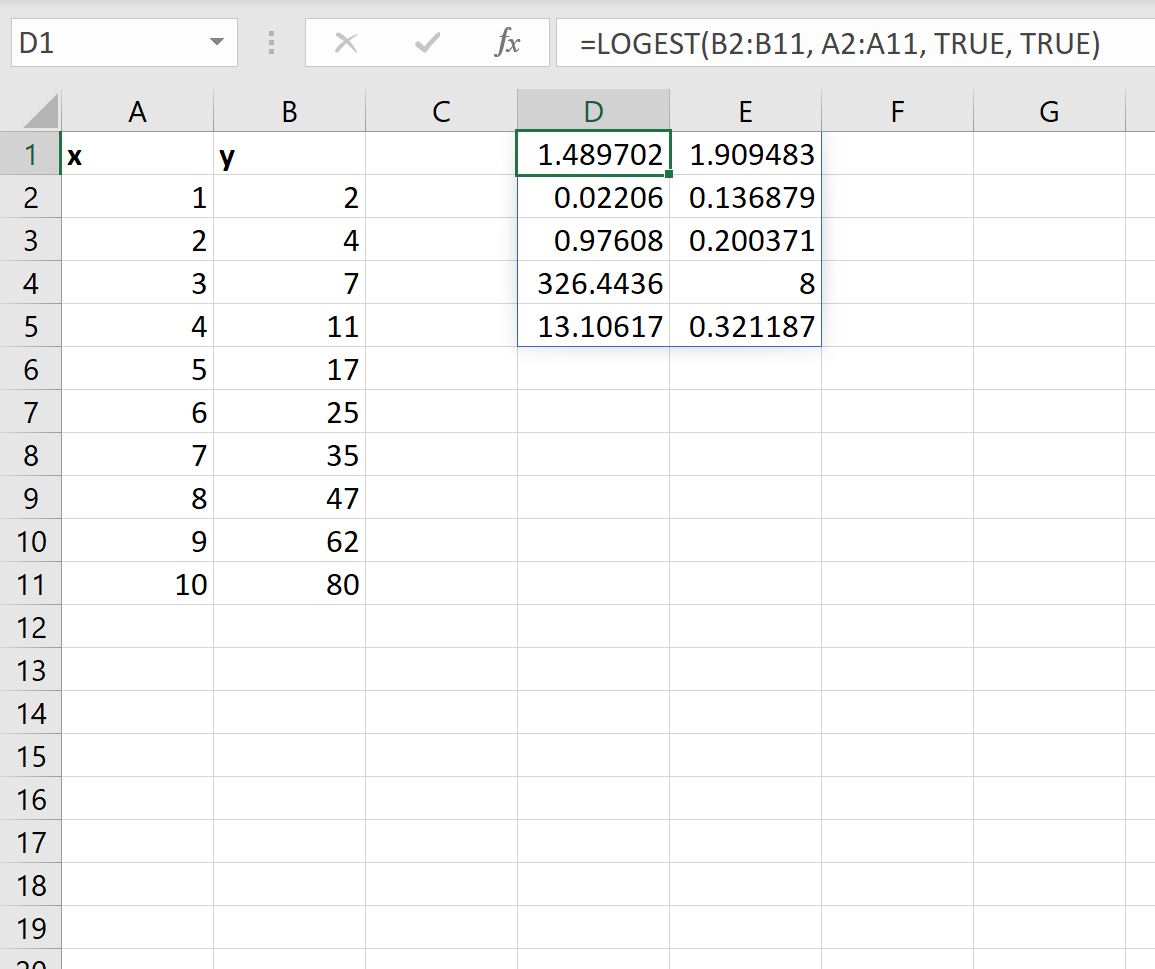
Ось як інтерпретувати кожне значення в результаті:

• Стандартна помилка для m становить 0,02206 .
• Стандартна помилка для b становить 0,136879 .
• R ² моделі становить .97608 .
• Стандартна помилка для y становить 0,200371 .
• Статистика F дорівнює 326,4436 .
• Ступенів свободи дорівнює 8 .
• Сума квадратів регресії дорівнює 13,10617 .
• Залишкова сума квадратів дорівнює 0,321187 .

Загалом, мірою, що представляє найбільший інтерес у цій додатковій статистиці, є значення R ² , яке представляє частку дисперсії у змінній відповіді, яку можна пояснити змінною предиктора.

Значення R ² може змінюватися від 0 до 1.

Оскільки R ² цієї конкретної моделі близький до 1, це говорить нам про те, що змінна предиктора x добре прогнозує значення змінної відповіді y.

За темою: що таке хороше значення R-квадрат?

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові операції в Excel:

Як використовувати DEVSQ в Excel
Як використовувати SUMSQ в Excel
Як виконати нелінійну регресію в Excel