Як виконати регресію ols у python (з прикладом)

Звичайна регресія найменших квадратів (МНК) — це метод, який дозволяє нам знайти лінію, яка найкраще описує зв’язок між однією або декількома змінними предиктора та змінною відповіді .

Цей метод дозволяє нам знайти таке рівняння:

ŷ = b ₀ + b ₁ x

золото:

• ŷ : оцінене значення відповіді
• b ₀ : Початок лінії регресії
• b ₁ : Нахил лінії регресії

Це рівняння може допомогти нам зрозуміти зв’язок між предиктором і змінною відповіді, і його можна використовувати для прогнозування значення змінної відповіді, враховуючи значення змінної предиктора.

Наступний покроковий приклад показує, як виконати регресію OLS у Python.

Крок 1: Створіть дані

Для цього прикладу ми створимо набір даних, що містить такі дві змінні для 15 студентів:

• Загальна кількість вивчених годин
• Результат іспиту

Ми виконаємо регресію OLS, використовуючи години як змінну прогнозу та оцінку іспиту як змінну відповіді.

Наступний код показує, як створити цей підроблений набір даних у pandas:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Крок 2: Виконайте регресію OLS

Далі ми можемо використати функції в модулі statsmodels для виконання регресії OLS, використовуючи години як змінну предиктора та оцінку як змінну відповіді :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Зі стовпця coef ми можемо побачити коефіцієнти регресії та написати таке підігнане рівняння регресії:

Оцінка = 65,334 + 1,9824*(години)

Це означає, що кожна додаткова вивчена година пов’язана зі збільшенням середнього балу на іспиті на 1,9824 бали.

Початкове значення 65 334 говорить нам про середній очікуваний іспитовий бал для студента, який навчається нуль годин.

Ми також можемо використати це рівняння, щоб знайти очікуваний бал за іспит на основі кількості годин, які навчається студент.

Наприклад, студент, який навчається протягом 10 годин, повинен отримати іспитовий бал 85,158 :

Оцінка = 65,334 + 1,9824*(10) = 85,158

Ось як інтерпретувати решту короткого опису моделі:

• P(>|t|): це значення p, пов’язане з коефіцієнтами моделі. Оскільки p-значення для годин (0,000) менше 0,05, можна сказати, що існує статистично значущий зв’язок між годинами та балом .
• R-квадрат: Це говорить нам про те, що відсоток варіації оцінок на іспитах можна пояснити кількістю вивчених годин. У цьому випадку 83,1% варіації балів можна пояснити вивченими годинами.
• F-статистика та p-значення: F-статистика ( 63.91 ) і відповідне p-значення ( 2.25e-06 ) говорять нам про загальну значущість регресійної моделі, тобто чи корисні змінні предикторів у моделі для пояснення варіації. у змінній відповіді. Оскільки p-значення в цьому прикладі менше 0,05, наша модель є статистично значущою, і години вважаються корисними для пояснення варіації оцінки .

Крок 3: Візуалізуйте найкращу лінію

Нарешті, ми можемо використати пакет візуалізації даних matplotlib , щоб візуалізувати лінію регресії, підігнану до фактичних точок даних:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

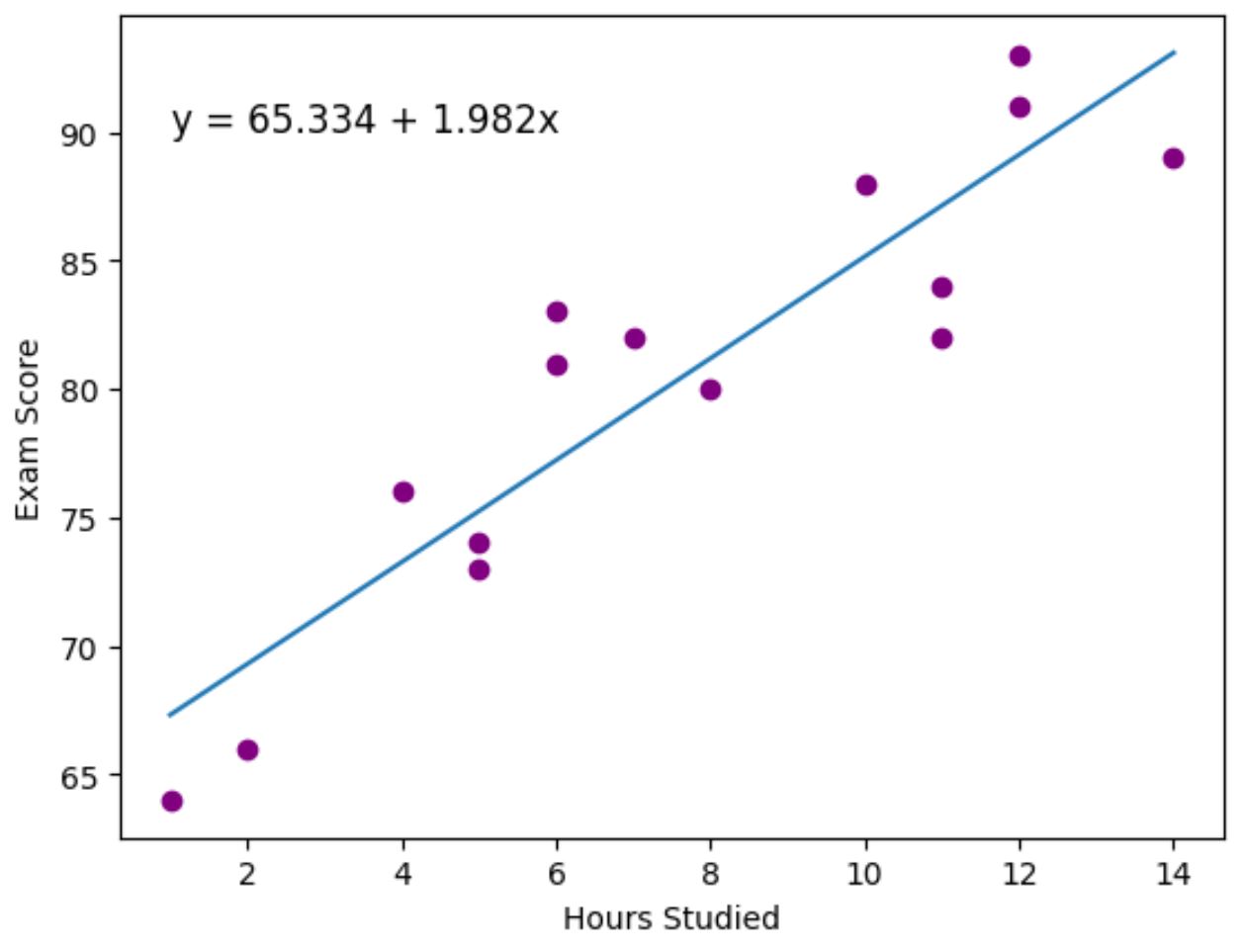
Фіолетові крапки представляють фактичні точки даних, а синя лінія представляє підігнану лінію регресії.

Ми також використали функцію plt.text() , щоб додати підігнане рівняння регресії у верхній лівий кут графіка.

Дивлячись на графік, здається, що підібрана лінія регресії досить добре відображає зв’язок між змінною годин і змінною оцінки .

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в Python:

Як виконати логістичну регресію в Python
Як виконати експоненціальну регресію в Python
Як розрахувати AIC регресійних моделей у Python