Як використовувати метод elbow в r для пошуку оптимальних кластерів

Один із найпоширеніших алгоритмів кластеризації в машинному навчанні відомий як кластеризація k-середніх .

Кластеризація K-означає – це техніка, за якої ми поміщаємо кожне спостереження з набору даних в один із K кластерів.

Кінцева мета полягає в тому, щоб мати K кластерів, у яких спостереження всередині кожного кластера досить подібні одне до одного, тоді як спостереження в різних кластерах досить відрізняються одне від одного.

Під час кластеризації k-середніх першим кроком є вибір значення для K – кількості кластерів, у які ми хочемо розмістити спостереження.

Один із найпоширеніших способів вибору значення для K відомий як метод ліктя , який передбачає створення графіка з кількістю кластерів на осі абсцис і загальною сумою квадратів на осі у, а потім визначення де в сюжеті з’являється «коліно» або поворот.

Точка на осі X, де виникає «коліно», вказує нам оптимальну кількість кластерів для використання в алгоритмі кластеризації k-середніх.

У наступному прикладі показано, як використовувати метод ліктя в R.

Приклад: використання методу ліктя в R

Для цього прикладу ми використаємо набір даних USArrests , вбудований у R, який містить кількість арештів на 100 000 осіб у кожному штаті США у 1973 році за вбивства, напади та зґвалтування, а також відсоток населення кожного штату, що проживає в містах. області. , UrbanPop.

Наступний код показує, як завантажити набір даних, видалити рядки з відсутніми значеннями та масштабувати кожну змінну в наборі даних, щоб отримати середнє значення 0 і стандартне відхилення 1:

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Щоб знайти оптимальну кількість кластерів для використання в алгоритмі k-середніх, ми використаємо функцію fviz_nbclust() із пакету factoextra , щоб створити графік залежності кількості кластерів від загальної суми квадратів:

 library (cluster)
library (factoextra)

#create plot of number of clusters vs total within sum of squares
fviz_nbclust(df, kmeans, method = “ wss ”) 

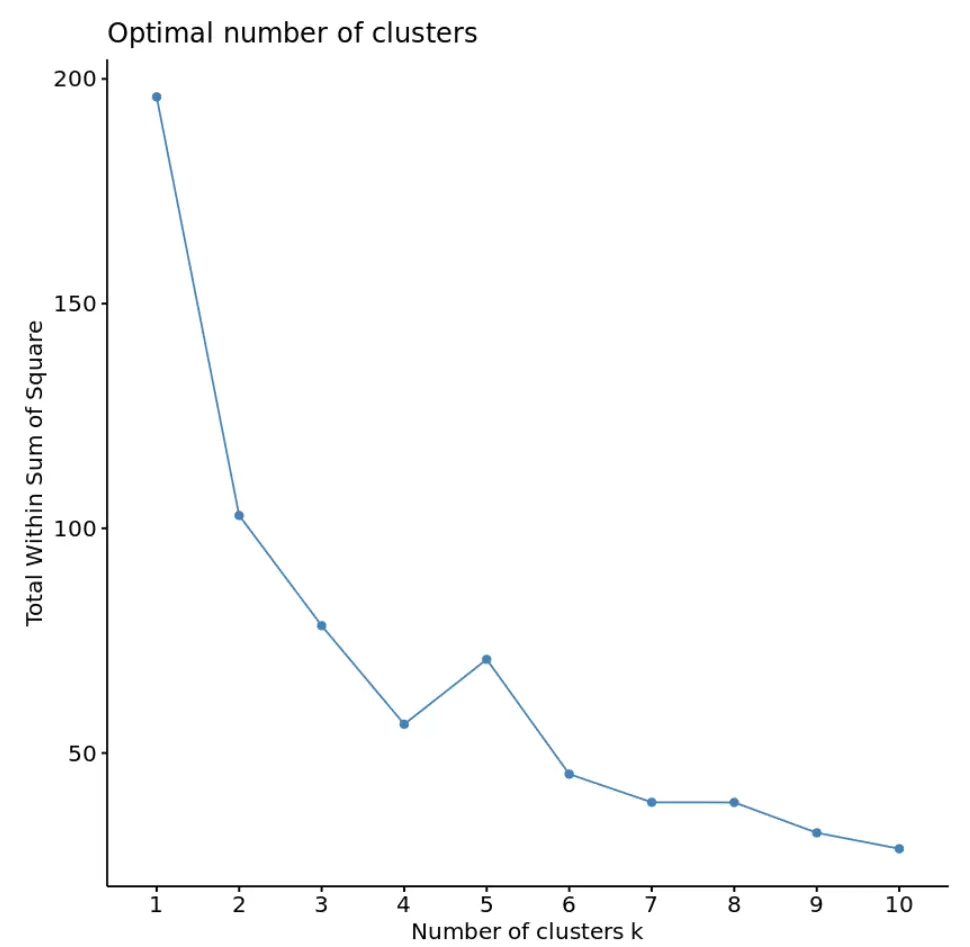
На цьому графіку видно, що є «коліно» або згин на k = 4 кластерах. Це точка, де підсумок у сумі квадратів починає стабілізуватися.

Це говорить нам про те, що оптимальна кількість кластерів для використання в алгоритмі k-середніх становить 4.

Примітка . Хоча ми могли б отримати нижчу підсумкову суму квадратів, використовуючи більше кластерів, ми б, ймовірно, переобладнали навчальні дані , і тому алгоритм k-середніх не працюватиме так добре на тестових даних.

Ми можемо використати функцію kmeans() із пакета кластерів , щоб виконати кластеризацію k-середніх на наборі даних, використовуючи оптимальне значення для k , рівне 4:

 #make this example reproducible
set. seeds (1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

З результатів ми бачимо, що:

• До першого кластеру було віднесено 16 держав
• До другого кластеру віднесено 13 держав
• До третього кластеру віднесено 13 держав
• До четвертого кластеру віднесено 8 держав

Ми також можемо додати кластерні призначення кожного стану до вихідного набору даних:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Кожне спостереження з вихідної бази даних було поміщено в одну з чотирьох груп.

Додаткові ресурси

Наступні навчальні посібники надають покрокові приклади того, як запускати різні алгоритми кластеризації в R:

Кластеризація K-середніх у R: покроковий приклад
Кластеризація K-Medoids у R: покроковий приклад
Ієрархічна кластеризація в R: покроковий приклад